5.5. Średniokwadratowa aproksymacja trygonometryczna

W zagadnieniach, w których funkcja jest okresowa wygodnie jest taką funkcję aproksymować nie wielomianami algebraicznymi, a wielomianami trygonometrycznymi - tym bardziej, że ich odchylenie kwadratowe od funkcji jest najmniejsze w porównaniu z odchyleniami kwadratowymi dla innych wielomianów.

Jeżeli funkcja o okresie
jest określona na dyskretnym zbiorze punktów i dane punkty są równoodległe, to korzystając z warunków ortogonalności (rozdz. 4.6) zbioru funkcji: łatwo obliczamy współczynniki wielomianu trygonometrycznego

(5.96)

jako rozwiązanie układu normalnego (5.67). Wyrażają się one następującymi wzorami:

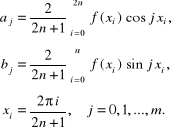
(5.97)

Zadanie aproksymacji funkcji określonej na dyskretnym zbiorze punktów wielomianem trygonometrycznym (5.96) jest realizowane w programie 5.3 (będącym zmodyfikowanym programem 4.4), którego tabulogram jest następujący:

{Program 5.3}

unit Obliczenia;

interface

uses

Windows, Messages, SysUtils, Classes, Graphics, Controls,

Forms, Dialogs, StdCtrls, Buttons, OleCtnrs;

type

Tabl1 = array[0..250] of Real;

Tabl2 = array[0..1000] of Real;

. . . . . . . . . . . . . . . . .

var

Form3: TForm3;

i,j,k,n,n1,nn,m,Q,st,tr,X0,Y0,ZX,ZY: Integer;

a,al,am,b,bl,h,odch,th,x,y: Real;

af,bf,ck,sk,xp,yp: Tabl1;

xx,yy,Xekr,Yekr: Tabl2;

plik,plik1: Text;

implementation

uses Ustawienia, Informacje, Grafika, Podglad;

{$R *.DFM}

{function f(x: Real): Real;}

procedure fsico(k: Integer; x: Real; var ck,sk: Tabl1);

var

i: Integer;

co,si: Real;

label kon;

begin

co:=Cos(x); si:=Sin(x);

ck[0]:=1; sk[0]:=0;

if k=0 then goto kon;

for i:=1 to k do begin

ck[i]:=co*ck[i-1]-si*sk[i-1];

sk[i]:=si*ck[i-1]+co*sk[i-1];

end;

kon:

end;

. . . . . . . . . . . . . . . . . . . . . .

procedure TForm3.BitBtn1Click(Sender: TObject);

begin

Form2.Show;

AssignFile(plik,Edit7.Text);

AssignFile(plik1,Edit5.Text);

Rewrite(plik); Rewrite(plik1);

Writeln(plik,'PROGRAM 5.3.');

Writeln(plik,'Średniokwadratowa aproksymacja trygonometryczna.');

Writeln(plik,'Dyskretny zbiór punktów rozłożonych równomiernie.');

Writeln(plik); a:=StrtoFloat(Edit1.Text);

b:=StrtoFloat(Edit2.Text); n:=StrtoInt(Edit3.Text);

m:=StrtoInt(Edit4.Text); am:=StrtoFloat(Edit6.Text);

Writeln(plik,'Początek przedziału: a = ',a:13);

Writeln(plik,'Koniec przedzialu: b = ',b:13);

Writeln(plik,'Liczba punktów: n = ',n:3);

Writeln(plik,'Stopień wielomianu: m = ',m:3);

nn:=2*n; n1:=nn+1; h:=(b-a)/n1;

if CheckBox1.Checked then Randomize;

Writeln(plik1,n1:3);

for i:=0 to n1 do begin

x:=a+i*h;

if CheckBox1.Checked then

y:=f(x)*(1+am*(0.5-Random));

if CheckBox1.Checked=False then y:=f(x);

xp[i]:=x; yp[i]:=y;

xx[i+1]:=x; yy[i+1]:=y;

end;

Q:=n1+2; al:=2*Pi/n1;

xx[n1+2]:=0; yy[n1+2]:=0;

for j:=0 to m do begin

th:=j*al;

af[j]:=0; bf[j]:=0;

fsico(nn,th,ck,sk);

for i:=0 to nn do begin

af[j]:=af[j]+yp[i]*ck[i];

bf[j]:=bf[j]+yp[i]*sk[i];

end;

af[j]:=2*af[j]/n1;

bf[j]:=2*bf[j]/n1;

end;

odch:=0;

Writeln(plik,'Wyniki aproksymacji funkcji:');

Writeln(plik,' i x[i] y[i] błąd');

for i:=0 to n1 do begin

x:=a+i*h; th:=i*al;

fsico(m,th,ck,sk); y:=af[0]/2;

for j:=1 to m do

y:=y+af[j]*ck[j]+bf[j]*sk[j];

bl:=f(x)-y; odch:=odch+Sqr(y-yp[i]);

Writeln(plik,i:3,' ',x:13,' ',y:18,' ',bl:13);

Q:=Q+1; xx[Q]:=x; yy[Q]:=y;

end;

Writeln(plik);

Writeln(plik,'Odchylenie kwadratowe: ',odch:13);

for k:=1 to 2*n1+3 do

Writeln(plik1,xx[k]:13,' ',yy[k]:13);

CloseFile(plik); CloseFile(plik1);

Form2.Wyniki.Lines.LoadFromFile(Edit7.Text);

end;

. . . . . . . . . . . . . . . . . . . . . . .

procedure TForm3.BitBtn3Click(Sender: TObject);

begin

Close;

end;

end.

Wczytywane z formularza Dane (rys. 5.19) liczby sterujące przebiegiem obliczeń stanowią zbiór czterech liczb:

a - początek przedziału,

b - koniec przedziału,

n - liczba określająca odstęp między równoodległymi punktami,

m - stopień wielomianu trygonometrycznego (5.96).

Rezultaty aproksymacji funkcji zestawionych w tablicy 5.1 oraz funkcji (4.51) po wczytaniu n = 50 oraz m = 5 przedstawione są na rysunkach 5.20 ÷ 5.23. Ponadto na rysunkach 5.24 ÷ 5.27 pokazane są wykresy wielomianów trygonometrycznych ap-roksymujących dyskretne zbiory punktów dla tych samych funkcji, zaburzonych losowo z amplitudą 0.2 (wygładzanie „chmury” danych eksperymentalnych).

Rys. 5.19

Rys. 5.20

Rys. 5.21

Rys. 5.22

Rys. 5.23

Rys. 5.24

Rys. 5.25

Rys. 5.26

Rys. 5.27

*

Analiza harmoniczna funkcji ciągłej polega na obliczaniu współczynników wielomianu trygonometrycznego (5.96) za pomocą wzorów:

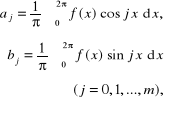
(5.98)

gdyż jest:

Obliczanie całek (5.98) może być jednak uciążliwe, szczególnie gdy funkcja jest określona w sposób dyskretny na nierównomiernym zbiorze punktów. Całki te mogą być w obliczone z dużą dokładnością, jeżeli funkcję przybliżymy interpolacyjną lub aproksymacyjną funkcją sklejaną trzeciego stopnia Ma-my więc:

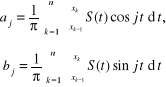
i następnie po wykorzystaniu przedstawienia funkcji sklejanej w postaci (4.103) otrzymujemy:

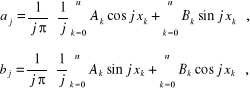
312 5. Rożniczkowanie, całkowanie i aproksymacja

5.5. Średniokwadratowa aproksymacja trygonometryczna 313

---