4.10. Hiperboliczna funkcja sklejana

Hiperboliczna funkcja sklejana należy do grupy tzw. uogólnionych funkcji sklejanych trzeciego stopnia, które charakteryzują się tym, że w ich równaniach występują pewne dodatkowe parametry, pozwalające na uzyskiwanie funkcji sklejanych o różnych, szczególnych własnościach. Istotny jest przy tym fakt, że funkcje te zachowują najważniejsze własności funkcji sklejanej trzeciego stopnia, tzn. prostotę i efektywność realizacji algorytmów w obliczeniach maszynowych.

Na mocy wzoru (4.67) stwierdzamy, że hiperboliczna funkcja sklejana spełnia na każdym odcinku równanie różniczkowe :

(4.126)

Po dwukrotnym scałkowaniu (4.126) i wyznaczeniu stałych całkowania z warunków:

(4.127)

mamy

(4.128)

W wyniku ponownego scałkowania (4.128), po uwzględnieniu warunków interpolacji otrzymujemy równanie hiperbolicznej funkcji sklejanej

(4.129)

oraz jej pochodnej

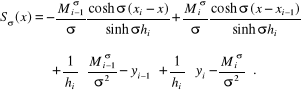
(4.130)

Występujące we wzorze (4.129) funkcje hiperboliczne uzasadniają używaną nazwę tych funkcji.

Obliczając z (4.130) lewo- i prawostronną pochodną w punkcie

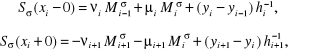
(4.131)

gdzie:

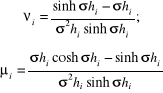
z warunku ciągłości pierwszych pochodnych: (i = 1, 2, ...,
n − 1) otrzymujemy układ równań na nieznane wartości

(4.132)

Do układu (4.132) należy dołączyć jeszcze dwa dodatkowe równania - podobnie jak w przypadku poprzednio rozpatrywanych funkcji sklejanych trzeciego stopnia.

Równania te można otrzymać z warunku okresowości funkcji lub, najczęściej, z następujących warunków brzegowych:

1) zadane pierwsze pochodne:

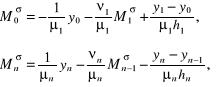
(4.133)

2) zadane drugie pochodne:

(4.134)

3) ciągłość trzecich pochodnych w węzłach i

(4.135)

Rozwijając w wyrażeniach określających wielkości i występujące tam funkcje hiperboliczne w szeregi potęgowe i następnie przechodząc do granicy
stwierdzimy, iż , a Dla równanie (4.129) przyjmuje więc postać równania funkcji sklejanej trzeciego stopnia (4.74) ÷ (4.75), natomiast dla równanie (4.129) dąży do równania funkcji sklejanej pierwszego stopnia (4.63); hiperboliczna funkcja sklejana łączy zatem w sobie zalety wielomianowych funkcji sklejanych stopni: pierwszego i trzeciego.

Na zakończenie napiszemy jeszcze równanie, analogiczne do (4.95), wprowadzając oznaczenia:
dla

Przy wykorzystaniu wzorów (4.131) piszemy układ równań:

(4.136)

względem i Obliczając następnie
i
i żądając ciągłości drugiej pochodnej otrzymamy:

(4.137)

*

Zadanie wyznaczania drugich pochodnych hiperbolicznej funkcji sklejanej, określonej układem równań (4.132) z warunkami brzegowymi (4.133) - (4.135), jest realizowane w procedurze:

Pochodne3(n,xw,yw,der2,sigma,utw0,utwn,al0,aln,der0,dern),

działającej podobnie jak procedura Pochodne2, umieszczona w Programie 4.5.

Sens parametrów formalnych procedury:

n - liczba węzłów (liczona od zera),

xw,yw[0..n] - tablice zawierające odcięte i rzędne zadanych punktów,

der2[0..n] - tablica zawierająca wyznaczane drugie pochodne

sigma - zmienna identyczna z parametrem

utw0,utwn - zmienne typu całkowitego określające rodzaj przyjętych warunków brzegowych; dla zadanych wartości tych zmiennych wynoszących 0, 1 lub 2 korzysta się, odpowiednio, z warunków (4.135), (4.133) lub (4.134),

al0,aln - zadane kąty nachylenia stycznych (w stopniach) dla x = a oraz x = b dla warunków (4.133),

der0,dern - zadane drugie pochodne dla x = a oraz x = b, jeśli wykorzystywane są warunki (4.134).

Po wyznaczeniu w procedurze Pochodne3 wartości drugich pochodnych hiperbolicznej funkcji sklejanej, za pomocą procedury FunSklej3 można obliczyć dla dowolnego
wartości funkcji oraz jej pochodnych
i
według wzorów (4.128) ÷ (4.130). Sens parametrów formalnych procedury Fun-Sklej3 jest identyczny z sensem parametrów formalnych procedur Pochodne3
i FunSklej2.

Procedury Pochodne3 i FunSklej3 zostały wykorzystane w programie 4.6 - przeznaczonym, tak samo jak program 4.5, do interpolowania funkcji (4.32) określonej punktami dyskretnymi dla

{Program 4.6}

unit Obliczenia;

interface

uses

Windows, Messages, SysUtils, Classes, Graphics, Controls,

Forms, Dialogs, StdCtrls, Buttons, OleCtnrs;

type

Tabl1 = array[0..200] of Real;

Tabl2 = array[1..1000] of Real;

. . . . . . . . . . . . . . . . .

var

Form3: TForm3;

i,j,K,n,m,utw0,utwn,X0,Y0,ZX,ZY: Integer;

a,b,bl,h,sigma,x,y,y1,y2: Real;

xx,yy,Xekr,Yekr: Tabl2;

der2,xw,yw: Tabl1;

plik,plik1: Text;

implementation

uses Ustawienia, Informacje, Grafika, Podglad;

{$R *.DFM}

function f(x: Real): Real;

begin

if Form3.RadioButton3.Checked then

f:=100*x*x*Exp(-10*x);

if Form3.RadioButton4.Checked then

f:=1/(1+25*x*x);

if Form3.RadioButton5.Checked then

f:=16*x*x*(x-1)*(x-1);

end;

function Sinh(x: Real): Real;

begin

Sinh:=(Exp(x)-Exp(-x))/2;

end;

function Cosh(x: Real): Real;

begin

Cosh:=(Exp(x)+Exp(-x))/2;

end;

procedure Pochodne3(n: Integer; xw,yw: Tabl1; var der2: Tabl1;

sigma: Real; utw0,utwn: Integer;

al0,aln,der0,dern: Real);

var

h1,h2,dy1,dy2,r1,r2,s1,s2,t1,t2: Real;

a0,an,p,p1,p2,w,w1,w2: Real;

a,c,d,q,u: Tabl1;

i,n1: Integer;

begin

n1:=n-1;

for i:=1 to n1 do begin

h1:=xw[i]-xw[i-1]; h2:=xw[i+1]-xw[i];

dy1:=yw[i]-yw[i-1]; dy2:=yw[i+1]-yw[i];

t1:=sigma*h1; t2:=sigma*h2;

p1:=Sinh(t1); p2:=Sinh(t2);

w1:=t1*sigma*p1; w2:=t2*sigma*p2;

r1:=(p1-t1)/w1; r2:=(p2-t2)/w2;

s1:=(t1*Cosh(t1)-p1)/w1;

s2:=(t2*Cosh(t2)-p2)/w2;

w:=1/(s1+s2);

a[i]:=r1*w; c[i]:=r2*w;

d[i]:=(dy2/h2-dy1/h1)*w;

end;

if utw0=0 then begin

h1:=xw[1]-xw[0];

h2:=xw[2]-xw[1];

p:=Sinh(sigma*h2);

s1:=-Sinh(sigma*h1)/p;

r1:=Sinh(sigma*(h1+h2))/p;

p:=1+a[1]*r1;

c[1]:=(c[1]+a[1]*s1)/p;

d[1]:=d[1]/p;

end;

if utwn=0 then begin

h1:=xw[n]-xw[n1];

h2:=xw[n1]-xw[n-2];

p:=Sinh(sigma*h2);

s2:=-Sinh(sigma*h1)/p;

r2:=Sinh(sigma*(h1+h2))/p;

p:=1+c[n1]*r2;

a[n1]:=(a[n1]+c[n1]*s2)/p;

d[n1]:=d[n1]/p;

end;

if utw0=1 then begin

a0:=al0*Pi/180; a0:=Sin(a0)/Cos(a0);

h1:=xw[1]-xw[0]; t1:=sigma*h1;

p1:=Sinh(t1); w1:=t1*sigma*p1;

r1:=(p1-t1)/w1; s1:=(t1*Cosh(t1)-p1)/w1;

p1:=1/(1-a[1]*r1/s1); c[1]:=c[1]*p1;

d[1]:=(d[1]-a[1]*((yw[1]-yw[0])/h1/s1-a0/s1))*p1;

end;

if utwn=1 then begin

an:=aln*Pi/180; an:=Sin(an)/Cos(an);

h2:=xw[n]-xw[n1]; t2:=sigma*h2;

p2:=Sinh(t2); w2:=t2*sigma*p2;

r2:=(p2-t2)/w2; s2:=(t2*Cosh(t2)-p2)/w2;

p2:=1/(1-c[n1]*r2/s2); a[n1]:=a[n1]*p2;

d[n1]:=(d[n1]-c[n1]*(an/s2-(yw[n]-yw[n1])/h2/s2))*p2;

end;

if utw0=2 then d[1]:=d[1]-a[1]*der0;

if utwn=2 then d[n1]:=d[n1]-c[n1]*dern;

q[1]:=-c[1]; u[1]:=d[1];

for i:=2 to n1 do begin

w:=1/(1+a[i]*q[i-1]);

q[i]:=-c[i]*w;

u[i]:=(d[i]-a[i]*u[i-1])*w;

end;

der2[n1]:=u[n1];

for i:=n1-1 downto 1 do

der2[i]:=der2[i+1]*q[i]+u[i];

if utw0=0 then der2[0]:=r1*der2[1]+s1*der2[2];

if utwn=0 then der2[n]:=r2*der2[n1]+s2*der2[n-2];

if utw0=1 then

der2[0]:=-a0/s1-r1*der2[1]/s1+(yw[1]-yw[0])/

(s1*(xw[1]-xw[0]));

if utwn=1 then

der2[n]:=an/s2-r2*der2[n1]/s2-(yw[n]-yw[n1])/

(s2*(xw[n]-xw[n1]));

if utw0=2 then der2[0]:=der0;

if utwn=2 then der2[n]:=dern;

end;

procedure FunSklej3(n: Integer; sigma,x: Real;

var y,y1,y2: Real; xw,yw,der2: Tabl1);

var

i,j: Integer;

c1,c2,h,h1,h2,s,s1,s2,t1,t2,u1,u2: Real;

label omin;

begin

for j:=1 to n do begin

i:=j; h1:=x-xw[i-1]; h2:=xw[i]-x;

if (h1>=0) and (h2>=0) then goto omin;

end;

omin:

h:=xw[i]-xw[i-1];

s:=Sinh(sigma*h); s1:=Sinh(sigma*h1);

s2:=Sinh(sigma*h2); c1:=Cosh(sigma*h1);

c2:=Cosh(sigma*h2); u1:=der2[j]*s1/s;

u2:=der2[i-1]*s2/s; y2:=u1+u2;

t1:=yw[i-1]-der2[i-1]/sigma/sigma;

t2:=yw[i]-der2[i]/sigma/sigma;

u1:=u1/sigma/sigma; u2:=u2/sigma/sigma;

y:=u1+u2+t1*h2/h+t2*h1/h;

y1:=(-der2[i-1]*c2+der2[i]*c1)/sigma/s-t1/h+t2/h;

end;

. . . . . . . . . . . . . . . . . . . . . . . . . .

procedure TForm3.BitBtn1Click(Sender: TObject);

begin

Form2.Show;

AssignFile(plik,Edit7.Text);

AssignFile(plik1,Edit6.Text);

Rewrite(plik); Rewrite(plik1);

a:=StrtoFloat(Edit1.Text); b:=StrtoFloat(Edit2.Text);

n:=StrtoInt(Edit3.Text); m:=StrtoInt(Edit4.Text);

sigma:=StrtoFloat(Edit5.Text);

Writeln(plik,'PROGRAM 4.6.');

Writeln(plik,'Interpolacja funkcji jednej zmiennej.');

Writeln(plik,'Hiperboliczna funkcja sklejana.');

Writeln(plik);

Writeln(plik,'Parametr funkcji: sigma = ',sigma:13);

Writeln(plik,'Początek przedziału: a = ',a:13);

Writeln(plik,'Koniec przedziału: b = ',b:13);

Writeln(plik,'Liczba węzłów: n = ',n:3);

Writeln(plik,'Liczba punktów wykresu: m = ',m:3);

Writeln(plik1,n:3); Writeln(plik1,m:3);

Writeln(plik);

h:=(b-a)/n;

for i:=0 to n do begin

x:=a+i*h; y:=f(x);

xw[i]:=x; yw[i]:=y;

xx[i+1]:=x; yy[i+1]:=y;

end;

xx[n+2]:=0; yy[n+2]:=0; K:=n+2;

Writeln(plik,'Wyniki interpolacji funkcji:');

Writeln(plik,' i x[i] y[i] błąd');

Pochodne3(n,xw,yw,der2,sigma,0,0,0,0,0,0);

h:=(b-a)/m;

for i:=0 to m do begin

x:=a+i*h; if i=m then x:=b;

FunSklej3(n,sigma,x,y,y1,y2,xw,yw,der2);

bl:=f(x)-y;

Writeln(plik,i:3,' ',x:13,' ',y:16,' ',bl:13);

K:=K+1; xx[K]:=x; yy[K]:=y;

end;

for i:=1 to m+n+3 do

Writeln(plik1,xx[i]:13,' ',yy[i]:13);

CloseFile(plik); CloseFile(plik1);

Form2.Wyniki.Lines.LoadFromFile(Edit7.Text);

end;

. . . . . . . . . . . . . . . . . . . . . . .

procedure TForm3.BitBtn3Click(Sender: TObject);

begin

Close;

end;

end.

Przykładowe wyniki obliczeń uzyskane za pomocą programu 4.6 są reprezentowane tablicami liczbowymi, które zawierają załączone tabulogramy komputerowe.

PROGRAM 4.6.

Interpolacja funkcji jednej zmiennej.

Hiperboliczna funkcja sklejana.

Parametr funkcji: sigma = 1.0000E-0001

Początek przedziału: a = -1.0000E+0000

Koniec przedziału: b = 1.0000E+0000

Liczba węzłów: n = 20

Liczba punktów wykresu: m = 100

Wyniki interpolacji funkcji:

i x[i] y[i] błąd

0 -1.0000E+0000 3.8461538E-0002 -6.7075E-0012

1 -9.8000E-0001 3.9999374E-0002 -1.5368E-0005

2 -9.6000E-0001 4.1616060E-0002 -1.8722E-0005

3 -9.4000E-0001 4.3323555E-0002 -1.4763E-0005

4 -9.2000E-0001 4.5133823E-0002 -7.4688E-0006

5 -9.0000E-0001 4.7058824E-0002 1.0970E-0011

6 -8.8000E-0001 4.9110520E-0002 5.3933E-0006

7 -8.6000E-0001 5.1300876E-0002 7.4877E-0006

8 -8.4000E-0001 5.3641853E-0002 6.2159E-0006

9 -8.2000E-0001 5.6145416E-0002 2.8154E-0006

10 -8.0000E-0001 5.8823529E-0002 1.3642E-0011

11 -7.8000E-0001 6.1689923E-0002 3.9171E-0007

12 -7.6000E-0001 6.4765384E-0002 1.4557E-0006

13 -7.4000E-0001 6.8072464E-0002 1.0553E-0006

14 -7.2000E-0001 7.1633717E-0002 -4.7964E-0007

15 -7.0000E-0001 7.5471698E-0002 -7.6852E-0011

16 -6.8000E-0001 7.9612146E-0002 5.6887E-0006

17 -6.6000E-0001 8.4093537E-0002 1.0752E-0005

18 -6.4000E-0001 8.8957534E-0002 1.0437E-0005

19 -6.2000E-0001 9.4245800E-0002 4.9074E-0006

20 -6.0000E-0001 1.0000000E-0001 -8.3332E-0011

21 -5.8000E-0001 1.0626750E-0001 2.4226E-0006

22 -5.6000E-0001 1.1311848E-0001 3.6910E-0006

23 -5.4000E-0001 1.2062881E-0001 -1.5477E-0006

24 -5.2000E-0001 1.2887437E-0001 -8.3873E-0006

25 -5.0000E-0001 1.3793103E-0001 2.0395E-0010

26 -4.8000E-0001 1.4789040E-0001 3.8594E-0005

27 -4.6000E-0001 1.5890687E-0001 7.5646E-0005

28 -4.4000E-0001 1.7115054E-0001 8.2333E-0005

29 -4.2000E-0001 1.8479155E-0001 5.1335E-0005

30 -4.0000E-0001 2.0000000E-0001 1.6644E-0010

31 -3.8000E-0001 2.1696350E-0001 -4.3757E-0005

32 -3.6000E-0001 2.3593951E-0001 -9.0458E-0005

33 -3.4000E-0001 2.5720301E-0001 -1.3360E-0004

34 -3.2000E-0001 2.8102895E-0001 -1.3007E-0004

35 -3.0000E-0001 3.0769231E-0001 6.4529E-0010

36 -2.8000E-0001 3.3752251E-0001 3.1533E-0004

37 -2.6000E-0001 3.7106673E-0001 6.8048E-0004

38 -2.4000E-0001 4.0892662E-0001 9.0945E-0004

39 -2.2000E-0001 4.5170382E-0001 7.8487E-0004

40 -2.0000E-0001 5.0000000E-0001 2.1091E-0009

41 -1.8000E-0001 5.5405426E-0001 -1.5680E-0003

42 -1.6000E-0001 6.1265529E-0001 -2.8992E-0003

43 -1.4000E-0001 6.7422918E-0001 -3.0882E-0003

44 -1.2000E-0001 7.3720204E-0001 -1.9079E-0003

45 -1.0000E-0001 8.0000000E-0001 -6.8212E-0010

46 -8.0000E-0002 8.6059893E-0001 1.4700E-0003

47 -6.0000E-0002 9.1517376E-0001 2.2574E-0003

48 -4.0000E-0002 9.5944914E-0001 2.0893E-0003

49 -2.0000E-0002 9.8914970E-0001 9.4931E-0004

50 5.1159E-0013 1.0000000E+0000 -1.7553E-0009

. . . . . . . . . . . . . . . . . . . . . . . . .

PROGRAM 4.6.

Interpolacja funkcji jednej zmiennej.

Hiperboliczna funkcja sklejana.

Parametr funkcji: sigma = 5.0000E+0000

Początek przedziału: a = -1.0000E+0000

Koniec przedziału: b = 1.0000E+0000

Liczba węzłów: n = 20

Liczba punktów wykresu: m = 100

Wyniki interpolacji funkcji:

i x[i] y[i] błąd

0 -1.0000E+0000 3.8461538E-0002 0.0000E+0000

1 -9.8000E-0001 3.9981054E-0002 2.9520E-0006

232 4. Interpolacja

4.10. Hiperboliczna funkcja sklejana 233

---