Logika (Pragmatyczna)
Literatura:
1. Kazimierz Ajdukiewicz - Logika Pragmatyczna,
2. Henry Cabat - Wybrane Elementy Logiki,
3. Henryk Cabat, Janusz Sobiecki - Wybrane zagadnienia z logiki (90 procent programu),
4. Tadeusz Kotrabiński - Kurs Logiki dla prawników (zalecane zapoznanie się z tym),
5. Zdzisław Ziębiński - Logika Praktyczna,
6. Pod red. Witolda Marciszewskiego - Mała encyklopedia Logiki,
7. Jeży Kmita - Wykłady z logiki i metodologii nauk.
Temat 1: Przedmiot Logiki, jej zakres i charakterystyka podstawowych działów.
Logika - Zasadniczym przedmiotem zainteresowań logiki jest analiza i rekonstrukcja ludzkich sposobów myślenia i rozumowania, które zostały już określone w sposób uzewnętrzniony ( najczęściej w postaci językowych wypowiedzi). Tak więc zasadniczym zadaniem logiki będzie analiza i wypracowanie obiektywnych kryteriów oceny poprawności głoszonych sądów, stosowanych rozumowań czy nawet działań z punktu widzenia możliwości określenia ich prawdy lub fałszu.
Rozumowanie - Rozumowaniami w interpretacji logicznej nazywać będziemy takie procesy intelektualne w których na podstawie sądów - zdań, wypowiedzi o określonej wartości logicznej ( prawdziwych lub fałszywych) formułować będziemy inne sądy, których wartość logiczna ( prawdy lub fałszu) zależy od tych pierwszych.
Logika wykład II
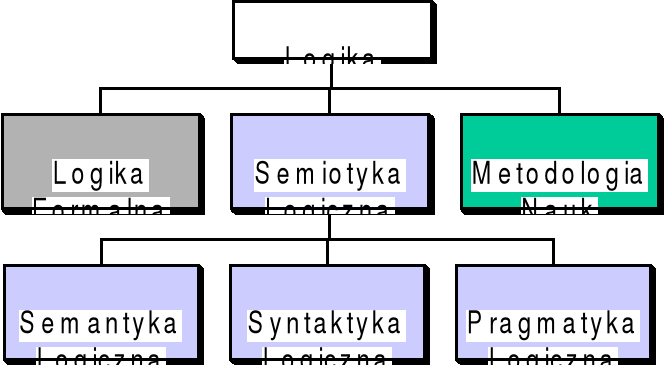
W zakresie szeroko rozumianego pojęcia logiki wyróżnia się najczęściej takie podstawowe działy jak:
Logika formalna
W zakresie logiki formalnej znajdują się rozważania dotyczące sposobów formułowania i analizy tak zwanych formalnych schematów rozumowań niezawodnych (np.: klasyczny rachunek zdań, rachunek nazw, rachunek predykatów...) oraz formalnych schematów rozumowań zawodnych ( w postaci np.: logiki indukcyjnej, logiki modalnej, logiki erotetycznej, logik wielowartościowych itp.)
Semiotyka logiczna
W zakresie szeroko rozumianej semiotyki logicznej (interpretowanej najczęściej jako tak zwana ogólna teoria znaków) wyróżnia się najczęściej takie działy jak:
Semantyka Logiczna
Syntaktyka Logiczna
Pragmatyka Logiczna
Semantyka logiczna
W zakresie semantyki logicznej znajdować się będą rozważania dotyczących treściowych i zakresowych założeń, jakie zachodzą pomiędzy wyrażeniami językowymi, a rzeczywistością pozajęzykową, do której wyrażenia te się odnoszą ( semantyczna analiza języka dotyczy przede wszystkim tak zwanej znaczeniowej strony języka).
Syntaktyka logiczna
W zakresie syntaktyki logicznej znajdować się będą rozważania dotyczące analizy zależności, jakie zachodzą pomiędzy wyrażeniami językowymi w procesie komunikowania. Syntaktyka logiczna określana jest też niekiedy mianem składni ( gramatyki logicznej). Jej zasadniczym zadaniem jest analiza tak zwanych podstawowych i pochodnych kategorii syntaktycznych oraz ich wpływów na wartość logiczną formułowanych sądów, wypowiedzi złożonych, narracji, itp.
W ramach syntaktyki logicznej najczęściej zajmować się będziemy analizą i wpływem struktury formalnej wypowiedzi oraz ocena z zakresu wypowiedzi na określenie stopnia jej poprawności lub fałszywości.
Pragmatyka logiczna
W zakresie pragmatyki logicznej znajdować się będą rozważania dotyczące zależności, jakie zachodzą pomiędzy wyrażeniami językowymi, a ludźmi, którzy posługują się tymi wyrażeniami językowymi w procesie komunikacji. Tak wiec zasadniczym przedmiotem zainteresowań pragmatyki logicznej będzie tak zwana prakseologiczna strona języka.
Logika wykład III
Temat: Język i jego logiczna struktura
Językiem określamy zazwyczaj taki system znaków w którym dana społeczność posługuje się w procesie komunikowania stale i o wszystkim.
Typologię ( klasyfikacje) języków przeprowadza się zazwyczaj z takich co najmniej dwóch punktów widzenia:
Ze względu na genezę i historyczne uwarunkowania oraz funkcjonowania danego języka.
Ze względu na sposób uzewnętrzniana się danego systemu językowego.
Biorąc pod uwagę pierwsze z wymienionych kryteriów wyróżnia się zazwyczaj takie podstawowe rodzaje języków jak:
języki naturalne (etniczne) - język powstał razem z daną grupa społeczną i razem z nią się rozwijał.
języki sztuczne - Takie które zostały celowo stworzone (np. Esperanto)
mieszane - np. język informatyków połączenie języka normalnego ze sztucznymi pojęciami.
Ze względu na formę uzewnętrzniania się danego języka wyróżniamy takie jego podstawowe rodzaje jak:
język werbalny (akustyczny)
język graficzny (pisany)
język gestowo-mimiczny (migowy)
W logicznej i semantycznej strukturze każdego języka możemy wyróżnić takie jego zasadnicze elementy jak:
Słownictwo (lingwistyka języka)
Reguły znaczeniowe (reguły semantyczne)
Reguły składniowe (reguły syntaktyczne)
Reguły transformacji (reguły wnioskowania, lub rozumowania)
W syntaktyczne strukturze języka wyróżniamy tak zwane podstawowe (zasadnicze) kategorie syntaktyczne oraz tak zwane pochodne (pomocnicze) kategorie syntaktyczne.
Do podstawowych kategorii syntaktycznych, a więc takich, które rozstrzygają o tym czy dany sąd, zdanie wypowiedź itp. są prawdziwe lub fałszywe należą:
Zdania
Nazwy
Kategorie te w istotny sposób decydują o tak zwanej komunikacyjnej sprawności języka. Pochodnymi (pomocniczymi) kategoriami syntaktycznymi są:
Funktory służące do budowy zdań, nazw, budowy wypowiedzi złożonych (narracji) czy też tak zwanych funktorów wyższego rzędu.
Operatory (kwantyfikatory), których zasadniczym zadaniem jest określenie zakresu obowiązywania danej nazwy, danego sądu, wypowiedzi złożonej itp.
Pomocnicze kategorie syntaktyczne zazwyczaj w procesie komunikowania nie funkcjonują samodzielnie, gdyż jak autonomiczne nie posiadają tak zwanego sensu logicznego. Służą natomiast wraz z innymi wyrażeniami (przede wszystkim nazwami i zdaniami) do tworzenia tak zwanych wyrażeń logicznie sensownych. (to znaczy takich, które możemy określić czy są prawdziwe czy fałszywe).
Logika IV
Zadania i wypowiedzi złożone, jako podstawowe kategorie syntaktyczne
Znak jako komunikat nie wystarczy. Żeby ten znak miał sens, to do tego znaku musi być dołączony określony komunikat, zdanie.
W rozumieniu logicznym zdaniem nazywać będziemy takie i tylko takie wyrażenia (wypowiedzi) w stosunku, do których możemy zastosować kryterium prawdy lub fałszu (a więc mamy nawet możliwość realną w sytuacjach wyjątkowo niepewnych określać ich stopień prawdopodobieństwa). W zakresie wypowiedzi określonych mianem logicznie sensownych będziemy wyróżniać tylko wypowiedzi (zdania) oznajmujące. Do wypowiedzi logicznie niepoprawnych (nie sensownych) zaliczane będą zarówno zdania pytajne, rozkazujące jak i wykrzyknikowe.
Logiczność pytań-polega na tym czy zawarte w nim treści są prawdziwe czy nie. Natomiast nie ma pytań głupich, są tylko głupie odpowiedzi.
W logice wyróżniamy podobnie jak w gramatyce j. Polskiego zarówno zdania proste jak i złożone. W logicznej interpretacji zdaniem prostym nazywamy takie wyrażenie w którego strukturze nie potrafimy wyróżnić takiej jego części właściwej, która może być samodzielnie zdaniem (wypowiedzią prawdziwą lub fałszywą) Zdaniem złożonym-nazywać będziemy takie wyrażenia, sądy, wypowiedzi itp. w których strukturze potrafimy wyróżnić takie części właściwe mogące być samodzielnie zdaniem.
Zdanie proste. 1. Jan jest studentem.
Zdanie złożone. 2. Nieprawda, że Jan jest studentem.
Zdanie złożone. 3. Jan jest studentem i studentką.
W logice wyróżniamy następujące rodzaje podstawowych wypowiedzeń złożonych, które są przyjmowane jako podstawa interpretacji prawdziwościowej większości przepisów prawa oceny kryteriów prawdziwości lub fałszywości wypowiedzeń złożonych itp.. Zdania te są również podstawą budowy tzw. formalnych struktur rozumowań niezawodnych i zawodnych.
Zdaniami są 1. Zdania złożone negacyjne, zbudowane w oparciu o funktor negacji - nieprawda, że - funktor ten w zastosowaniu logicznym powoduje zawsze, że wyrażenie, zdanie, sąd, wypowiedź itp. poprzedzone tym funktorem w przypadku, gdy jest prawdziwym przechodzi w zdanie, sąd, wypowiedź itp. fałszywą. W zapisie formalnym zdania te określa się przy pomocy symboli: ∾⊢┌ np. ∾p┌ p ⊢p
2. Zdanie złożone assercyjne zbudowane w oparciu o funktor - prawdą jest, że - funktor ten nie zmienia wartości logicznej wypowiedzi do której się odnosi, lecz jak gdyby dodatkowo „potwierdza” jej aktualną wartość logiczną. ◇◇P
3. Zdania złożone implikacyjne zbudowane najczęściej w oparciu o funktory - Jeżeli to... - to z tego wynika, że w rozumieniu logicznym konsekwencją związku implikacyjnego w danej wypowiedzi jest przede wszystkim i w pierwszym rzędzie jest związek pomiędzy wartościami logicznymi wypowiedzi składającymi się na wypowiedź złożoną, a nie tylko zależności treściowe pomiędzy tymi wypowiedziami.
Jeżeli 2x2=5, to W-w jest stolicą Anglii.
Jest to zdanie prawdziwe, bo wynik zdania, jak i zdanie pierwsze jest nieprawdziwe.
Jeżeli 2x2=4, to W-w jest stolicą Anglii.
Jest to zdanie nieprawdziwe ponieważ zdanie końcowe jest fałszywe niezależnie od pierwszego.
W zapisie formalnym funktor - jeżeli to - zapisujemy →← P→QP↔Q
Strzałka wskazuje zawsze kierunek wynikania.
Logika Wykład V
Temat: Zdania złożone cd.
4. Zadania złożone alternatywne. Są trzy rodzaje alternatywy:
Zadanie alternatyw nierozłącznej, zbudowanej o funktor lub. W zapisie będzie to + lub V na przykład p+q lub p V q.
Alternatywa rozłączna, zbudowana o funktor albo. W zapisie formalnym jest to Np.: p qDysjunkcja. Najmniej intuicyjne. Oparte na funktorze albo, albo. W zapisie formalnym jest to /. Np.: p/q
Zdanie złożone koniunkcyjne. Są zbudowane na funktorze i, wymagamy więc żeby wszystkie części zdania były prawdziwe, aby całe zdanie było prawdziwe. W zapisie formalnym jest to • lub Λ
Zdanie złożone ekwiwalencyjne (dwustronna implikacja) oparte na funktorze ekwiwalencji wtedy i tylko wtedy gdy, lub jest równoważne. Wyrażenia te będą prawdziwe wtedy gdy zakres tych zdań jest równoważny. Dana wypowiedź będzie prawdziwa kiedy ich treść będzie taka sama. W zapisie formalnym jest to ≡ lub .
Zdanie złożone według funkcji Pearsea lub Łukasiewicza. (zdanie złożone według funktora ani, ani). Jest ono prawdziwe jeśli wszystkie części zdania są fałszywe. Znak:↓
Temat: Nazwy i ich logiczna analiza.
Nazwami w rozumieniu logicznym nazywać będziemy takie wyrażenia, które w procesie komunikowania pełnią funkcję podmiotu lub orzecznika w zdaniu podmiotowo orzecznikowym typu a jest b (np.: Jan jest studentem) W literaturze spotkamy się z kilkunastoma nazwami nazw. Nas obowiązywać będzie klasyfikacja:
NAZWY
Konkretne Abstrakcyjne
Przedmiotowe Puste
Jednostkowe Ogólne Jednostkowe Ogólne
Nazwami konkretnymi nazywać będziemy takie wyrażenia, które w rzeczywistości pozajęzykowej reprezentują konkretne desygnaty lub denotaty. Desygnatem danej nazwy nazywać będziemy realnie istniejące przedmioty, istoty, zjawiska itp. do których daną nazwę stosujemy. (np. desygnatem nazwy mikrofon jest to co Cabak trzyma w ręku). Denotatem lub denotacją danej nazwy nazywać będziemy zbiór desygnatów, które tej nazwie przysługują. (np. denotatem nazwy mikrofon będzie wszystko co jest mikrofonowi podobne).
Nazwami przedmiotowymi nazywać będziemy takie nazwy konkretne, które w rzeczywistości pozajęzykowej posiadają realnie istniejące desygnaty.(np.: mikrofon)
Nazwami pustymi nazywać będziemy takie nazwy konkretne, które w rzeczywistości pozajęzykowej nie posiadają realnie istniejących desygnatów, natomiast reprezentują tak zwane świadomie wymyślone desygnaty wraz z opisem ich realnych i empirycznych cech. (np.: Krasnoludki, Smerfy, bo realnie czegoś takiego nie ma).
Jeżeli danej nazwie przysługuje tylko jedne desygnat, nazwę te określamy mianem jednostkowej. Jeżeli nazwie tej przysługuje więcej niż jeden desygnat, określamy ją mianem ogólnej. (np.: Nazwa ZEUS jest nazwa pusta, jednostkową bo dotyczy jednego boga, natomiast jeśli posługujemy się nazwą BOGOWIE, to jest to nazwa ogólna, ponieważ dotyczy wielu bogów) Imiona są nazwami jednostkowymi.
Nazwami abstrakcyjnymi nazywać będziemy wyrażenia, które w rzeczywistości pozajęzykowej nie posiadają realnych desygnatów, lecz posiadają tak zwaną denotację, gdyż zazwyczaj dotyczą:
zbioru cech danego zjawiska ( np.: białość, zieloność)
związków i zależności zachodzących pomiędzy cechami, zjawiskami itp. (np.: pożyteczny, wdzięczny)
Logika
Wykład VI
Temat: Charakterystyka pomocniczych kategorii syntaktycznych.
Funktory.
Funktory - funktorami nazywać będziemy takie pomocnicze kategorie syntaktyczne, które w połączeniu z innymi wyrażeniami służą do budowy logicznie sensownych wypowiedzi, nazw, czy też tak zwanych funktorów wyższego rzędu.
Podstawowa typologia funktorów:
Wyróżniamy takie podstawowe rodzaje funktorów jak:
funktory nazwotwórcze, które służą do budowy tak zwanych nazw złożonych. (np.: Student - jest nazwą, dobry student - nie jest tożsamy z nazwą student, czyli za pomocą funktora dobry tworzona jest nowa nazwa)
Funktory zdaniotwórcze, służące do budowy zdań złożonych, wypowiedzi złożonych, ale również i zdań prostych.(np.: Jan jest studentem, w tym zdaniu funktor jest jest funktorem zdaniotwórczym)
Funktory funktorotwórcze są to wyrażenia służące do budowy funktorów złożonych określanych niekiedy mianem funktorów wyższego rzędu. (Np. Słońce świeci, Słońce świeci jasno)
Operatory
Operatorami (kwantyfikatorami) nazywamy wyrażenia lub symbole, których zasadniczym zadaniem jest określenie zakresu obowiązywania danej nazwy, danego zdania, czy też wypowiedzi złożonej.
W logice wyróżniamy dwa podstawowe rodzaje kwantyfikatorów:
Kwantyfikator duży określany mianem generalizatora, który w brzmieniu werbalnym czytamy Dla każdego, każdy, dla wszystkich w zapisie formalnym:
Kwantyfikator mały określany mianem egzystencjalnego, w brzmieniu werbalnym czytamy dla niektórych, niektóry, istnieją takie że, w zapisie formalnym:
Temat: Przyczyny nieporozumień komunikacyjnych.
Przyczyny nieporozumień komunikacyjnych wyróżnia się zazwyczaj z takich dwóch punktów widzenia:
Są to tak zwane przyczyny o charakterze obiektywnym, których źródła tkwią w samej istocie języka i są niezależne zarówno od podmiotu posługującego się wyrażeniami językowymi jak i formami, sposobami stosowania wyrażeń językowych w procesie komunikowania.
Przyczyny o charakterze subiektywnym, których zasadniczym źródłem jest świadome, zamierzone, czy też nieświadome i niezamierzone, wadliwe posługiwanie się wyrażeniami językowymi w procesie komunikowania.
Zasadniczym źródłem i przyczynami nieporozumień komunikacyjnych o charakterze obiektywnym są:
Funkcjonowanie wyrażeń językowych w procesie komunikowania na tak zwanych różnych poziomach odniesienia przedmiotowego - w różnych supozycjach językowych. Wyrażenie językowe w procesie komunikowania mogą bowiem funkcjonować w takich podstawowych supozycjach jak:
W supozycji realnej (przedmiotowej), w której dane wyrażenie językowe odnosimy do faktycznie występującego przedmiotu, istoty, zjawiska, zależności, itp.
W supozycji określanej mianem metajęzykowej, w której dane wyrażenie funkcjonuje do określenia treści lub znaczenia innych wyrażeń językowych.
W supozycji formalnej, w której wyrażenia językowe w procesie komunikowania służą do określenia związków i zależności, jakie zachodzą pomiędzy tymi wyrażeniami w tymże procesie.
Wiele nieporozumień wynika z tego, że odbiorca odbiera wyraz w supozycji innej niż zamierzaliśmy.
Tak zwana immanentna nieostrość wyrażeń językowych. (np.: osobowość, materia, kosmos itp.)
Zasadniczymi źródłami i przyczynami nieporozumień komunikacyjnych o charakterze subiektywnym najczęściej są:
świadome, czy nawet nieświadome posługiwanie się tak zwanymi wyrażeniami wieloznacznymi. Wieloznaczność wyrażeń może występować najczęściej w postaciach:
w postaci wieloznaczności zdań, lub wypowiedzi złożonych. Występuje to najczęściej w tedy, gdy dana wypowiedź ma słabo zkwantyfikowany zakres (np.: Szkoci są skąpi. )
Wieloznaczność nazw. (np.: zamek, morze(może), wilk)
Posługiwanie się celowe, lub nawet nie zamierzone tak zwanymi wyrażeniami relatywnymi (np.: ładny, brzydki, pożyteczny)
Błąd ekwiwokacji - polegający na tym, że to samo wyrażenie językowe zostało użyte przynajmniej kilkakrotnie przez nadawcę komunikatu, lecz za każdym razem w innej supozycji językowej, co doprowadziło, że odbiorca komunikatu interpretował to pojecie nie w tej supozycji, jak była w intencji nadawcy komunikatu (przykład z grą w Brydża).
Wadliwe posługiwanie się tak zwanymi wyrażeniami okazjonalnymi (np.: Tam, gdzieś, za chwilę, itp.), w sytuacjach, gdy kontekst wypowiedzi w których one występują, nie określa jednoznacznie ich aktualnej interpretacji.
Błąd amfibologii (amfibli) - polegający na tym, że wypowiedź została wadliwie sformułowana pod względem gramatycznym, gdyż o treści tej wypowiedzi decydują znaki interpunkcji, a nie wszystkie wyrażenia użyte do jej budowy (np.: Zatrzymać nie wolno strzelać, Zatrzymać, nie wolno strzelać, lub Zatrzymać nie wolno, strzelać).
Zamierzone, lub nie zamierzone posługiwanie się tak zwanymi niedopowiedzeniami. (np.: Wrócę o ósmej, Sprzedam Ci zamek, itp.)
Formułowanie wypowiedzi określanych mianem logicznie nie sensownych, lub absurdalnych (np.: najniższą budowlą w Warszawie jest pałac kultury).
Gdy w danym języku funkcjonuje wyrażenie, którym na ogół potrafimy się poprawnie posługiwać, lecz jego treść lub zakres rozumiemy w sposób intuicyjny, a zależy nam tym, żeby tą treść i zakres określić w miarę jak najprecyzyjniej.
Gdy chcemy do naszego systemu językowego wprowadzić nowe wyrażenie językowe, bądź to dla opisu nowo poznanych zjawisk, bądź też dla wzbogacenia funkcjonującego sytemu językowego.
Gdy chcemy całkowicie, lub częściowo zmienić znaczenie lub zakres wyrażeń już funkcjonujących w naszym języku.
Powinna być budowana według tak zwanej klasycznej, arystotelesowskiej, formuły definicji, która w przekładzie łacińskim brzmi: Definitio fit pergenus proximum et differentiam specificam (formuła ta w swobodnym przekładzie mówi że: Definiujemy poprzez dodanie do wyrażenia definiowanego wyrażeń, które są od niego genetycznie pierwotne i nadrzędne, oraz wyszczególnienie cechy lub cech najistotniejszych, najbardziej specyficznych dla definiowanego zjawiska, istoty, zależności itp.)
Powinna być budowana według tak zwanej klasycznej, arystotelesowskiej, formuły definicji, która w przekładzie łacińskim brzmi: Definitio fit pergenus proximum et differentiam specificam (formuła ta w swobodnym przekładzie mówi że: Definiujemy poprzez dodanie do wyrażenia definiowanego wyrażeń, które są od niego genetycznie pierwotne i nadrzędne, oraz wyszczególnienie cechy lub cech najistotniejszych, najbardziej specyficznych dla definiowanego zjawiska, istoty, zależności itp.) (przykład: Człowiek, jest to istota posiadająca umiejętność logicznego myślenia. lub Kwadrat jest to prostokąt równoboczny) W logicznej strukturze każdej definicji wyróżniamy takie elementy jak:
Definiendum - wyrażenia, zjawiska, zależności, itp. definiowane (Człowiek, kwadrat)
Łącznik definicyjny, lub tak zwany funktor identyczności
Definiens - wyrażenia, zjawiska, zależności itp. definiujące.
Poprawnie zdefiniowana definicja powinna spełniać tak zwane formalne warunki poprawności. Warunkami tymi są:
Warunek adekwatności (równoznaczności lub równoważności), polegający na tym, że dana definicja jest adekwatna wtedy, kiedy pomiędzy definiensem a definiendum występuje tak zwana zamienność znaczeniowa lub zakresowa.
Warunek różnokształtności polegający na tym, że w definiensie nie mogą znajdować się wyrażenia takie same lub synonimiczne, jak w definiendum
Poprawnie sformułowana definicja powinna również spełniać tak zwane poza formalne dydaktyczne warunki poprawności. Warunkami takimi są:
Warunek komunikatywności definicji - polegający na tym, że w definiensie nie powinny znajdować się wyrażenia tak samo nieznane lub nawet mniej znane, dla odbiorcy definicji jak w definiendum.
Warunek mocy wyjaśniającej definicji (eksplikacyjności) - polegający na tym, że definiens powinien w sposób bardziej jasny i prosty wyjaśniać znaczenie i zakres definiendum niż było to dotychczas.
Gdy nie spełnimy formalnego warunku adekwatności definicji, najczęstszymi błędami będą
Zbudujemy definicję za szeroką, w której definiens będzie nadrzędny w stosunku do definiendum (np.: Człowiek jest istotą).
Zbudujemy definicję za wąska, w której definiens, jest podrzędny do definiendum (np.: Biologia jest to nauka zajmująca się strukturą kwiatów).
Zbudujemy definicję krzyżującą się, w której zakresy definiensa i definiendum, zachodzą na siebie, lecz się nie pokrywają (np.: Student jest to sportowiec)
Możemy zbudować tak zwaną definicję wykluczającą się. (np.: Szpada jest to pół automatyczna broń palna. Demokracja jest to ustrój, w którym podstawową formą władzy jest dyktatura.)
W przypadku, gdy nie spełnimy formalnego warunku różnokształtności definicji, w procesie definiowania najczęściej możemy popełnić takie błędy jak:
Błędne koło w definiowaniu bezpośrednie, którego szczególnie charakterystycznym przypadkiem jest błąd typu. (Idem per idem - to samo przez to samo)
Błędne koło w definiowaniu pośrednie, w rodzaju „a jest to b, b jest to c, c jest to d, d jest to a”.
W przypadku niespełnienia poza formalnych (dydaktycznych) warunków poprawności definicji, w procesie definiowania możemy popełnić takie zasadnicze błędy jak:
Błąd określany mianem „ignotum per ignotum” (nieznane przez nieznane) (np.: Ekstrawersja to odwrotność introwersji)
Zbudujemy tak zwaną definicje rozmyta, czy nawet tak zwaną pseudo definicję, określaną też niekiedy mianem bełkotu semantycznego.
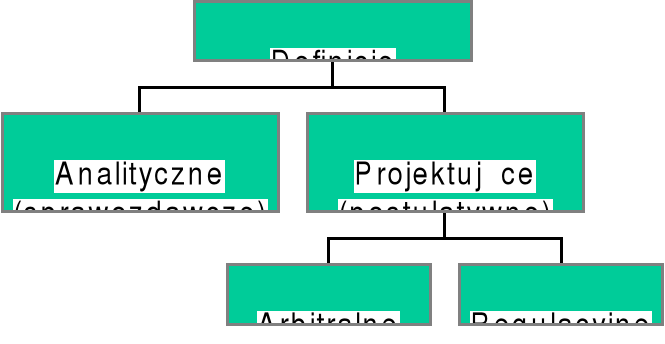
Cel definiowanyBudowę definiendum - wyróżniamy takie definicje jak:
definicje wyraźne, w których jako definiendum występuje tylko jedno wyrażenie.
Definicje kontekstowe, w których definiendum składa się z więcej niż jednego wyrażenia językowego.
Supozycję językową, w której formułowana jest dana definicja - wyróżniamy takie rodzaje definicji jak:
definicje realne (przedmiotowe), które w sposób niejako bezpośredni, charakteryzują realnie istniejące przedmioty, zjawiska, rzeczy itp.
definicje nominalne (słownikowe), które służą do określenia zasadniczych treści lub zakresu wyrażenie lub wyrażeń definiowanych.
Sposób wykorzystania rzeczywistości pozajęzykowej w procesie definiowania - wyróżniamy takie podstawowe rodzaje definicji jak:
definicje ostensywne, charakteryzujące się tym, że treść definicji jest bezpośrednio powiązana z prezentacją lub pokazem prezentowanego zjawiska.
Definicje operacyjne, których treścią jest opis działania lub operacji jakie należy zrealizować, by wyjaśnić definiowane zjawisko.
Weryfikacji sprawdzanego sadu (hipotezy)(verun - prawda) Istotą weryfikacji jest to, że w procesie sprawdzania w oparciu o empirycznie obserwowalne fakty 100 % potwierdziliśmy prawdziwość sprawdzanego sądu (hipotezy)
Sprawdzany sąd zastał skonfirmowany (w określonym stopniu uprawdopodobniony)
Sprawdzany sąd został sfalsyfikowany ( z łaciny fałsz). Istotą tego sprawdzana jest wykazanie, że sprawdzany sąd na podstawie aktów empirycznych trzeba uznać za fałszywy. Jest tak najczęściej w przypadku sprawdzania tak zwanych sądów ogólnych (generalizujących), których fałszywość musimy uznać na podstawie stwierdzenia niezgodnych z nimi faktów szczegółowych.
Wyjaśnienie. Wyjaśnieniem nazywać będziemy te rodzaje rozumowań, których zasadniczym zadaniem jest próba odpowiedzi na pytanie typu „dlaczego”. W logicznej strukturze wyjaśniania wyróżniamy takie dwa zasadnicze elementy:
eksplanandum - wyrażenia, zjawiska, zależności, itp. wyjaśniane
eksplanans - wyrażenia, zjawiska, zależności, itp. wyjaśniające
wyjaśninie „dedukcyjne”, którego charakterystyczną cechą jest to, że w formie eksplanansu występują prawa nauki lub zasady czy też reguły powszechnie uznawane w określonych dyscyplinach naukowych
wyjaśnianie probabilistyczne (prawdopodobne) charakteryzujące się tym, że w formie eksplanansu występują prawa, zasady lub reguły uzasadniane w oparciu o teorię prawdopodobieństwa lub tzw. zależności statystyczne
wyjaśnienie genetyczne polegające na tym, że w eksplanansie znajduje się genetyczny ciąg zdarzeń, przyczyn, itp., które traktujemy jako wystarczającą podstawę wyjaśnienia interesującego nas zjawiska, np.: ewolucyjna teoria Darwina
wyjaśnianie funkcjonalne polegające na tym, że w eksplanansie znajduje się opis funkcji lub działań, które należy zrealizować by wyjaśnić interesujące nas zjawiska
Rozumowania indukcyjne. Rozumowaniami indukcyjnymi nazywać będziemy takie rozumowania, w których na podstawie stwierdzenia lub eliminacji określonej ilości faktów, zjawisk szczegółowych, formułujemy tzw. uogólniony sąd indukcyjny.
Kanon jedynej zgodności, polegający na tym, że o zależności pomiędzy zjawiskiem A i B możemy orzec wtedy, gdy w zakresie zjawiska A potrafimy wyróżnić taką cechę A1, która gdy wystąpi pociąga zawsze za sobą wystąpienie zjawiska B.
Kanon jedynej różnicy, polegający na tym, że o zależności pomiędzy zjawiskiem A i B możemy orzec wtedy, gdy w zakresie zjawiska A potrafimy wyróżnić taką cechę A1, której brak pociąga za sobą wystąpienie zjawiska B.
Kanon jedynej zgodności i jedynej różnicy. Są to jak gdyby dwa poprzednio omówione kanony stosowane w rozumowaniu łącznie. Z metodologicznego punktu widzenia kanon ten jest traktowany jako mocna postawa dla stwierdzenia związku zachodzącego pomiędzy dwoma lub więcej zjawiskami.
Kanon zmian współtowarzyszących, polegający na tym, że o zależności pomiędzy zjawiskiem A i B możemy orzec wtedy, gdy w zakresie zjawiska A potrafimy wyróżnić taką cechę A1, której zmiana stopnia natężenia pociąga za sobą proporcjonalne zmiany zachodzące w zakresie zjawiska B
Kanon reszt, polegający na tym, że w przypadku, gdy nie potrafimy w zakresie zjawiska A i B wyróżnić takich cech które świadczyły by o zachodzących między tymi zjawiskami związkach, a mimo tego jesteśmy nadal przekonani, że zależność między tymi zjawiskami istnieje, to mamy prawo rozumować, że istnieją jakieś nieznane nam jeszcze cechy (reszty), których należy poszukiwać bo one będą świadczyć o tych intuicyjnie przez nas uznawanych zależnościach.
zmienne zdaniowe, określane przy pomocy małych liter alfabetu łacińskiego (p, q, r, s ..), które reprezentują zdania w interpretacji logicznej.
Tak zwane stałe logiczne, w postaci podstawowych funktorów zdaniotwórczych np.: implikacji, alternatywy, koniunkcji, ekwiwalencji itp.
Całości, zbudowane ze zmiennych zdaniowych i stałych logicznych, w postaci tak zwanych funkcji zdaniowych. Wyróżniamy, takie podstawowe rodzaje funkcji zadaniowych jak:
Funkcje tożsamościowo prawdziwe (tautologie logiczne (prawa logiczne, tezy logiczne)), charakteryzujące się tym, że jako całości są zawsze wyrażeniami prawdziwymi
Funkcje tożsamościowo fałszywe (kontr tezy logiczne) charakteryzujące się tym, że jako całości są zawsze wyrażeniami fałszywymi
Funkcje spełnialne, charakteryzujące się tym, że wartość logiczna całości tych funkcji uzależniona będzie od wartości zmiennych zdaniowych (argumentów), oraz występujących pomiędzy nimi funktorów.
Ekwiwalencyjne p ≡ p ( 1 ≡ 1) = 1 ( 0 ≡ 0) =1
Implikacyjne p p ( 1 1) =1 ( 0 0 ) =1
Ontologiczną. W interpretacji ontologicznej prawo to mówi, że nie może być tak, żeby coś za razem istniało i nie istniało.
Interpretacja psychologiczna, zgodnie z którą, nie może być tak, zebyśmy o czymś myśleli i za razem nie myśleli
Interpretacja logiczna, zgodnie z którą nie może być tak, żeby dane zdanie było zarazem prawdziwe i fałszywe.
1
Prawo transpozycji prostej:
Prawa De Morgana dla rachunku zdań
Prawo
z
Zmienne nazwowe - określane przy pomocy dużych liter alfabetu łacińskiego S, P N, W itd., które reprezentują nazwy ogólne, lecz nie puste (przedmiotowe).
Funktory zdaniotwórcze - określane przy pomocy samogłosek a, i, e ,o. Samogłoski te są samogłoskami z dwóch wyrażeń łacińskich:
Affirmo - uznaje, twierdzę
Nego - nie uznaję, przeczę
Całości - zbudowane ze zmiennych nazwowych i funktorów zdaniotwórczych w postaci tak zwanych zdań kategorycznych. Wyróżniamy takie podstawowe rodzaje zdań kategorycznych jak:
Zdanie ogólno twierdzące - typu każde S jest P w zapisie formalnym: SaP
Zadnia szczegółowo twierdzące - typu niektóre S są P w zapisie formalnym: SiP
Zdania ogólno przeczące - typu żadne S nie jest P w zapisie formalnym: SeP
Zdania szczegółowo przeczące - typu niektóre S nie są P w zapisie formalnym: SoP
Rozumowaniami bezpośrednimi nazywać będziemy takie rozumowania w których w oparciu tylko o jedną przesłankę „Bezpośrednio” formułujemy wniosek.
Rozumowaniami pośrednimi nazywać będziemy takie rozumowania w których wniosek porty jest na więcej niż jednej przesłance. (np.: Każdy adwokat jest prawnikiem. W tej uczelni wykładają adwokacji. Możemy więc powiedzieć że w tej uczelni wykładają prawnicy.)
Wnioskowania przez konwersję (odwrócenie)
Wnioskowanie przez obwersje
Wnioskowania z opozycji w oparciu o tak zwany kwadrat logiczny
Przesłanki
Konkluzje
Tak zwany termin średni (M), to znaczy termin lub pojęcie, które jako identyczne występuje we wszystkich przesłankach, natomiast nie występuje w konkluzji. Termin ten rozstrzyga też o tak zwanym związku pomiędzy przesłankami.
przesłanki
konkluzje
tzw. termin średni (M), tzn. termin lub pojęcie, które jako identyczne występuje we wszystkich przesłankach natomiast nie występuje w konkluzji. Termin ten rozstrzyga też o tzw. związku pomiędzy przesłankami
obydwie przesłanki (wszystkie) nie mogą być przesłankami przeczącymi (co najmniej jedna musi być zdaniem twierdzącym)
obydwie przesłanki (wszystkie) nie mogą mieć charakteru szczegółowego (co najmniej jedna musi być zdaniem ogólnym)
termin średni (M) musi być występować w identycznej postaci we wszystkich przesłankach
konkluzja nie może być mocniejsza od najsłabszej przesłanki
jeżeli któraś z przesłanek była zdaniem przeczącym konkluzja nie może mieć charakteru zdania twierdzącego
jeżeli któraś z przesłanek miała charakter szczegółowy konkluzja nie może być zdaniem ogólnym
termin średni (M) nie może występować w konkluzji
Faza H T(P) Jeśli przyjmujemy, że znaleźliśmy to twierdzenie przechodzimy do 2 fazy
Faza T H
1
Dowód wprost, określany niekiedy w logice prawa jako tak zwany dowód prokuratorski, którego istota jest to, że jako kolejne przesłanki do dowodu przyjmowane są wszystkie wyrażenia występujące w toku postępowania dowodowego, aż do przedostatniego włącznie. Ostatnie wyrażenie traktowane jest jako wyrażenie dowodzone. Wykazanie, że wyrażenie to w sposób logicznie niezawodny wynika z wcześniej uznanych za prawdziwe przesłanek kończy dowód. Prawo sylogizmu hipotetycznego koniunkcyjnego
(p→q)
(q→r)
p założenie dowodu wprost (z. d. w.)q reguła obrywania do 1 i 3 (RO 1, 3)
r z 2,4 co było do udowodnienia (c. b. d. u.)
Dowód nie wprost, określany niekiedy mianem dowodu adwokackiego. Charakteryzuje się tym, ze jako kolejne przesłanki do dowodu przyjmowane są wszystkie wyrażenia występujące w toku postępowania dowodowego aż do ostatniego włącznie z tym, że ostatnie wyrażenie przyjmowane jest w postacie odwrotnej nie występuje faktycznie. Istotą tego typu dowodów jest wykazanie, że przyjęcie do dowodu ostatniego wyrażenia w postaci odmiennej niż w rzeczywistości nieuchronnie prowadzi do sprzeczności z wcześniej uznanymi za prawdziwe przesłankami. Właśnie wykazanie takowej sprzeczności traktowane jest jako dowód na prawdziwość ostatniego wyrażenia w jego oryginalnej postaci.
(p→q)
(q→r)
p
p założenie dowodu nie wprost (z. d. n. w.)q. 1,3
~q 2,4
Sprzeczność 5,6 (c. b. d. o.)
Dowody intuicyjne w których jako przesłanki przyjmowane są sądy powszechnie uznawane za prawdziwe, chociaż barak na to pełnego uzasadnienia.
Dowody entymematyczne (niezupełne) charakteryzujące się tym, że w toku postępowania dowodowego określona ilość przesłanek jest pomijana, traktowana jako z tych czy innych powodów oczywiste, co może być jednak przyczyną zawodności tego typu dowodów.
Dowody nie w pełni sformalizowane, które zazwyczaj charakteryzują się - nie każdy wiersz dowodu jest wykazany jako przesłanka w pełni udokumentowana i nie jest wykazane w jakim stopniu kolejny krok postępowania dowodowego jest konsekwencją wcześniej uznanych za prawdziwe przesłanek.
Czy Brutus zabił Cezara?
Jakie funkcje spełnia prawo?
Kiedy miesiąc luty miał 35 dni?
Ile kosztuje zamek?
niewiadomą pytania określaną przy pomocy tzw. partykuły pytajnej.
Daną pytania określaną mianem datum quastionis pytania, w której zawarta jest wiedza ze względu na którą określamy zakres niewiadomej pytania (W wypadku zdania pierwszego partykułą pytajną jest „Czy” a datum quastionis - dalsza część zdania).
Oceny ich logicznej poprawności
Oceny ich merytorycznej poprawności
Oceny ich prakseologicznej poprawności
Jest logicznie rozstrzygalne (logicznie sensowne)
Jest semantycznie poprawne
Jest syntaktycznie poprawne
Pytania rozstrzygnięcia, które rozpoczynają się od partykuły CZY, i na które zbiór możliwych odpowiedzi jest dwuelementową alternatywą rozłączną.
Pytania dopełnienia (uzupełnienia), które rozpoczynają się od partykuł pytajnych innych poza partykułą CZY i których zbiór odpowiedzi ma zazwyczaj postać bądź alternatywnej bądź koniunkcyjnej narracji.
Założenie jedyności, polegające na tym, że przyjmujemy iż z możliwych na to pytanie odpowiedzi przynajmniej jedna odpowiedź jest odpowiedzią prawdziwą.
Negatywne założenie pytania, polegające na tym, że przyjmujemy iż z możliwych na to pytanie odpowiedzi przynajmniej jedna będzie odpowiedzią fałszywą.
Założenie, że stwierdzamy iż jedna i tylko jedna z możliwych na to pytanie odpowiedzi jest odpowiedzią prawdziwą lub jedna i tylko jedna odpowiedź jest odpowiedzią fałszywą.
Źródła i genezę ich pochodzenia. Będą to najczęściej pytania określane mianem ze względu na:
rodzaj rzeczywistości badawczej (teoretyczne i praktyczne)
zakres danego pytania (otwarte, półotwarte, zamknięte)
przynależność do określonej dyscypliny naukowej (ekonomiczne, socjologiczne, biologiczne)
Ze względu na cel i sposób poszukiwani odpowiedzi na dane pytanie rozróżniamy takie podstawowe rozdaje pytań jak:
Pytania opisowe, które zazwyczaj zaczynają się od partykuł pytajnych co to jest, gdzie to jest, jakie to jest.
Pytania wyjaśniające (ekspalnacyjne) rozpoczynające się od partykuły pytającej dlaczego.
Pytania prakseologiczne, których zasadniczą treścią jest analiza ludzkiego działania, a więc dotyczą przede wszystkim celów działania, warunków działania, metod działania, oceny skutków działania itp.
Oceny potencjalnych i aktualnych możliwości udzielenia na dane pytanie odpowiedzi.
Określenia materialnych i czasowych możliwości udzielenia na dane pytanie odpowiedzi.
Określenia stopnia własnej kompetencyjności co do możliwości udzielenia na dane pytanie odpowiedzi.
Dowodzenie - będące procesem intelektualnym, którego zasadniczym celem jest wykazanie jaką faktyczną wartość ma dowodzony sąd (prawda lub fałsz) nie zależnie od tego kto ten sąd dowodzi i dla kogo jest dowodzony. Dowodzenie zawsze powinno mieć charakter obiektywny.
Argumentowanie - rozumiane jako czynność zmierzająca do wywołania u kogoś (u innych osób) określonych i pożądanych z naszego punktu widzenia przeświadczeń, ocen postaw itp. Argumentowanie ma zawsze formę spersonifikowaną, to znaczy skierowane jest do konkretnej osoby, osób, grup itp. W procesie argumentowania w szeregu przypadków przewagę uzyskują przewagę elementy o charakterze emocjonalnym i psychologicznym nad elementami racjonalnymi. Argumentowanie ze swej istoty ma zazwyczaj charakter subiektywny.
Powinien być w miarę jednoznacznie określony przedmiot dyskusji (temat)
Powinien być ustalony język dyskusji i poziom dyskusji.
Logika
Wykład VII
b) Formułowanie tak zwanych pojęć logicznie nie sensownych. W Interpretacji logicznej nie sensowność logiczna danej wypowiedzi polegać będzie na tym, że sformułowaliśmy, w której użyte zostały wyrażenia o wykluczających się treściach (sprzeczne, np.: Wierzący ateista, Syn bezdzietnej matki).
W prawie istnieje coś takiego jak nie sensowność emocjonalna sadu. Znaczy to , że nie można używać w jednym zdaniu, wyrażeń o różnym ładunku emocjonalnym (np.: Niech Wasza Ekscelencja zamknie mordę)
c) Formułowanie wypowiedzi jawnie fałszywych, określanych też niekiedy mianem absurdalnych (np.: Kwadratura koła). Wiele stwierdzeń uważanych obecnie za fałszywe, kiedyś były prawdziwe. Zmieniły to np.: nowe odkrycia.
W procesie komunikowanie zarówno z obiektywnych jak i subiektywnych przyczyn, najczęściej popełnianymi błędami o charakterze semantycznym będą:
Temat: Semantyczna teoria definicji i jej pragmatyczne zastosowanie.
Język Łaciński ma szerokie zastosowanie w medycynie w prawie, dlatego, że jest językiem bardzo konkretnym. Aby pojecie weszło do języka musi być bardzo dokładnie zdefiniowane.
Definicje.
Definicjami nazywać będziemy wyrażenia lub wypowiedzi, których zasadniczym zadaniem jest podanie informacji, o znaczeniu lub zakresie danego wyrażenia językowego, przez wskazanie innych wyrażeń językowych funkcjonujących w danym systemie komunikacyjnym, które mają takie same lub podobne znaczenie i zakres.
Z praktycznym procesem definiowania mamy najczęściej doczynienia w takich sytuacjach jak:
Poprawnie sformułowana definicja powinna spełniać takie warunki jak:
Logika VIII
(cd)
W procesie definiowania, gdy nie są przestrzegane omówione wyżej formalne i poza formalne warunki formułowania definicji możemy popełnić takie zasadnicze rodzaje błędów jak:
Logika
Wykład IX
Typologię definicji przeprowadza się najczęściej ze względu na takie kryteria jak:
Definicjom analitycznym przysługuje wartościowanie z punktu widzenia prawdy, lub fałszu.
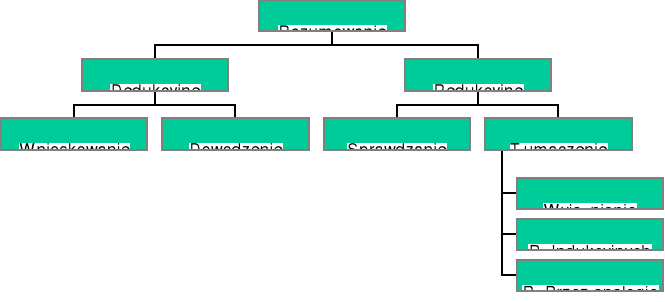
TEMAT: Rozumowania Logiczne i ich charakterystyka.
Rozumowaniami nazywać będziemy takie procesy intelektualne w których na podstawie sądów - zdań o określonej wartości logicznej (prawdziwych lub fałszywych), formułujemy inne sądy, których wartość logiczna zależy od tych pierwszych
Rozumowaniami dedukcyjnymi nazywać będziemy takie i tylko takie rozumowania, które mają charakter niezawodny to znaczy, gwarantują nam, że wnioski (konkluzje) wynikające z tych rozumowań są zawsze wnioskami prawdziwymi. W intuicji potocznej dedukcja utożsamiana jest zazwyczaj z tokiem postępowania według schematu „Od ogółu do szczegółu”. Cechą rozstrzygająca jest to że mają charakter niezawodny.
Rozumowaniami redukcyjnymi nazywać będziemy takie rozumowania, które mają charakter zawodny, to znaczy nie gwarantują nam prawdziwości formułowanych na jej podstawie wniosków, natomiast gwarantują że przy ich poprawnym stosowaniu stopień prawdopodobieństwa wniosków będzie wzrastał.
Sprawdzanie. Sprawdzaniem nazywamy rozumowanie redukcyjne, które realizowane jest najczęściej w tak zwanym procesie empirycznego sprawdzania sądów o nie ustalonej wartości logicznej (najczęściej tak zwanych hipotez) w oparciu o empirycznie potwierdzane i obserwowalne zjawiska. Sprawdzanie Realizowane jest najczęściej w takich postaciach jak:
LOGIKA WYKŁAD 10
TŁUMACZENIE I JEGO LOGICZNA STRUKTURA
Tłumaczeniem nazywać będziemy takie rozumowania redukcyjne, w których mając określone zjawisko jednostkowe czy też ciąg takowych zjawisk chcemy „wytłumaczyć” istotę tych zjawisk, fakt ich występowania itp. w oparciu o wcześniej uznane za prawdziwe tzw. racje (np.: prawa, reguły, ustawy, itp.), które traktujemy jako wystarczające podstawy poprawnego tłumaczenia. Najczęściej stosowanymi rodzajami tłumaczenia są:
Właśnie ze względu na charakter logicznego i merytorycznego związku pomiędzy eksplanandum a eksplanansem wyróżnia się zazwyczaj takie podstawowe rodzaje wyjaśniania jak:
Indukcją enumeracyjną (przez wyliczenie) nazywać będziemy takie rozumowania redukcyjne, w których na podstawie stwierdzenia występowania określonej ilości faktów, zjawisk szczegółowych formułujemy określony sad indukcyjny dotyczący rodzaju zależności zachodzących pomiędzy tymi zjawiskami i faktami szczegółowymi. W przypadku gdy uogólniony sąd indukcyjny oparty jest na pełnej (100%) liczbie faktów i zjawisk szczegółowych rozumowanie takie określamy mianem indukcji enumerycznej zupełnej. W przypadku zaś gdy sąd indukcyjny oparty jest na niepełnej, wybranej przez nas ilości faktów i zjawisk szczegółowych rozumowanie takie określamy mianem indukcji enumeracyjnej niezupełnej. Indukcja enumeracyjna zupełna jest jedynym przykładem rozumowania redukcyjnego, które ma charakter niezawodny (pewny). Indukcja enumeracyjna niezupełna jest zaś przykładem rozumowania zawodnego.
Indukcją eliminacyjną nazywać będziemy rozumowanie, które na podstawie „eliminacji” określonej ilości faktów i zjawisk szczegółowych oraz stwierdzenia związku pomiędzy tymi faktami formułujemy uogólniony sąd indukcyjny. Rozumowania określone mianem indukcji eliminacyjnej w praktyce realizowane są najczęściej w oparciu o tzw. kanony (zasady) J. S. Milla.
Logika
Wykład XI
Wyróżniamy takie podstawowe kanony Milla jak:
Rozumowaniami przez analogie nazywać będziemy takie rozumowania, których na podstawie stwierdzenia występowania faktów w określonym ciągu czasowym, przyczynowym, przestrzennym itp., które są pod określonym względem do siebie w jakimś stopniu podobne, wnioskujemy, że i występujące po nich kolejne fakty zdarzenia, zależności itp., też będą do nich podobne.
TEMAT: Rozumowania dedukcyjne i ich charakterystyka
Wnioskowanie - wnioskowaniem nazywamy takie rozumowania dedukcyjne, w których wychodząc od prawdziwych racji (przesłanek), przechodzimy zawsze od prawdziwych wniosków (konkluzji). Wnioskowania mają najczęściej postać tak zwanych formalnych schematów rozumowań niezawodnych, występujących najczęściej w systemie tak zwanego rachunku zdań, rachunku nazw, rachunku predykatów, teorii relacji itp.
Klasyczny rachunek zdań i jego formuły, jako przykład wnioskowań dedukcyjnych.
Sensownymi wyrażeniami w klasycznym rachunku zdań są:
Współcześnie przyjęto, że zdania (wypowiedzi) prawdziwe będą posiadały wartość oznaczaną liczbą 1, zdania uznawane za fałszywe oznaczane cyfrą 0.
Matryca prawdziwościowa dla klasycznego rachunku zdań.
p |
q |
∼ P |
◊ p |
p q |
p V q |
p ≠ q |
p / q |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
Logika
Wykład XII
Matryca prawdziwościowa dla klasycznego rachunku zdań.
p |
q |
∼ P |
◊ p |
p q |
p V q |
p ≠ q |
p / q |
pΛq |
p≡q |
p ↓ q, |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
Zdania negacyjne - są wyrażeniami prawdziwymi, wtedy gdy funktor negacji odnosi się do wyrażenia fałszywego.
Zdania implikacyjne - są fałszywe tylko w jednym przypadku, wtedy gdy poprzednik implikacji jest wyrażeniem prawdziwym natomiast następnik wyrażeniem fałszywym. W pozostałych sytuacjach wypowiedzi implikacyjne są zawsze prawdziwe.
Alternatywa nierozłączna jest fałszywa tylko w jednym przypadku, gdy wszystkie człony alternatywy są wyrażeniami fałszywymi. Prawdziwa jest zaś wtedy, gdy przynajmniej jeden z członów alternatywy jest prawdziwy.
Alternatywa rozłączna jest prawdziwa wtedy, gdy człony tej alternatywy mają różną wartość logiczną. Fałszywa zaś jest wtedy gdy jej człony mają tę samą wartość logiczną.
Dysjunkcja jest fałszywa tylko w jednym przypadku, gdy wszystkie człony dysjunkcji są prawdziwe. Prawdziwa zaś jest wtedy, gdy przynajmniej jeden z jej członów jest wyrażeniem fałszywym.
Koniunkcja jest wyrażeniem prawdziwym tylko w jednym przypadku, gdy wszystkie jej składniki są wyrażeniami prawdziwymi. Fałszywa zaś jest wtedy, gdy przynajmniej jedne składnik koniunkcji jest wyrażeniem fałszywym.
Ekwiwalencja jest wyrażeniem prawdziwym wtedy, gdy jej składniki mają tę samą wartość logiczną. Fałszywa zaś jest wtedy, gdy mają różną wartość logiczną.
Funkcja Ani, ani jest wyrażeniem prawdziwym tylko w jednym przypadku, gdy wszystkie jej składniki są wyrażeniami fałszywymi. Fałszywa zaś jest wtedy, gdy przynajmniej jeden ze składników jest wyrażeniem prawdziwym.
Prawa logiczne z jedną zmienną zdaniową.
- Prawo tożsamości:
- Prawo wyłączonego środka
p V~ p
1 V~ 1 0 V~0
(1 V 0)=1 (0 V 1)=1
- Prawo sprzeczności
~(pΛ~p)
Prawo to ma trzy interpretacje:
~(pΛ~p) ~(pΛ~p)
~(1Λ~1) ~(0Λ~0)
~(1Λ0) ~(0Λ1)
~(0) ~(0)
- Prawo redukcji do absurdu
(p ~p) ~p
Prawa logiczne z dwoma zmiennymi zdaniowymi:
( p q) ( ~q ~p)
Logiczna zasada transpozycji mówi o tym, że uznając prawdziwość określonego sądu implikacyjnego, należy również uznać prawdziwość innego sądu implikacyjnego, w którym poprzednik implikacji przeszedł w miejsce następnika implikacji ze znakiem negacji, natomiast następnik przeszedł w miejsce poprzednika też ze znakiem negacji.
p=1 q=1, ( 1 1) (~1 ~1) 1 (0 0); 1 1 1 |
p=1 q =0 (1 0 ) (~0 ~1) 0 ( 1 0 ) 0 0 1 |
p =0 q=1 (0 1) (~1 ~0) 1 ( 0 1) 1 1 1 |
p=0 q=0 (0 0) (~0 ~0 ) 1 ( 1 1 ) 1 1 1 |
~(p Λ q)(lub ≡) (~p V ~q)
P=1 q=1 ~(1 Λ 1) (~1 V ~1 ) ~(1) ( 0 V 0 ) 0 0 1 |
|
|
|
Logika
Wykład XIV
Temat: Schematy rozumowań dedukcyjnych oparte na rachunku nazw.
Schematy oparte na rachunku nazw (sylogistyka (sylogistyka Arystoteles)) - sensownymi wyrażeniami w rachunku nazw są:
W oparciu o powyższe zdania kategoryczne zbudowane zostały tak zwane schematy rozumowań bezpośrednich i pośrednich.
Logika
Wykład XV
Powyższe zdania kategoryczne mogą występować bądź w formie przesłanek bądź w formie wniosków (konkluzji). Gdy występują jako przesłanki, siła tych przesłanek ( stopień obowiązywania) jest w takiej hierarchii jak układ zdań kategorycznych (to znaczy najmocniejszą przesłanką jest zdanie ogólno twierdzące, słabszą przesłanką zdanie szczegółowo twierdzące, jeszcze słabszą ogólno przeczące i najsłabszą szczegółowo przeczące). Jest to istotne z tego względu, że zarówno w schematach wnioskowań bezpośrednich, jak i pośrednich obowiązuje generalna zasada dedukcji, że wniosek nie może być mocniejszy od najsłabszej przesłanki.
Z rozumowań bezpośrednich najczęściej stosowanymi schematami wnioskowań będą :
SaP PiS
SiP PiS
SeP PeS
SoP → P
SaP Se~P
SiP Si~P
SeP Sa~P
SoP Si~P
przeciwieństwa
SaP SeP
SiP SoP
podprzeciwieństwo
Logiczny stosunek przeciwieństwa mówi o tym, że dwa zdania przeciwne nie mogą posiadać rej samej wartości logicznej.
Logiczny stosunek sprzeczności mówi o tym ze dwa zdania sprzeczne nie mogą być za razem prawdziwe. Jedno musi być fałszywe.
Stosunek nadrzędności mówi o tym, że z prawdziwości zadania nadrzędnego musi zawsze wnikać prawdziwość zdania podrzędnego
Stosunek podrzędności mówi o tym, że z prawdziwości zadnia przędnego nic nie możemy wnioskować o wartości logicznej zdania nadrzędnego, natomiast z fałszywości zadnia podrzędnego możemy wnioskować o fałszywości zdania nadrzędnego
Stosunek podprzeciwieństwa rozstrzyga o tym, że z fałszywości zdania podprzeciwnego wynika prawdziwość zdania przeciwnego.
SaP ~SeP
SaP ~SoP
SaP SiP
SeP SoP
SeP ~SiP
SeP ~SaP
W oparciu o kwadrat logiczny można wyprowadzić 36 formuł.
Schematy rozumowań pośrednich mają postać struktur formalnych, w których wyróżnia się takie jak gdyby trzy zasadnicze elementy:
takie jak gdyby trzy zasadnicze elementy:
Poprawne rozumowania pośrednie powinny spełniać tzw. formalne warunki prawdziwości dotyczące przesłanek oraz konkluzji. Warunkami poprawności przesłanek są:
Warunkami poprawności konkluzji są:
Formalne struktury rozumowań pośrednich ułożono w tzw. figury i tryby.
I MP II MP II PM IV PM
SM MS SM MS
SP SP SP SP
I Barbara Darii Ferio Celarent Celeront Barbari
MaP MaP MeP MeP MeP MaP
SaM SiM SiM SaM SeM SaM
SaP SiP SoP SeP SoP SiP
Logika
Wykład XVI
Temat: Dowodzenie i jego interpretacja logiczna.
Dowodzeniem nazywamy takie rozumowanie dedukcyjne, w którym mając sąd o nieustalonej wartości logiczne poszukujemy dla niego racji (uzasadnienia) o którym wiemy, że jest ono prawdziwe i następnie wykazujemy, że ten dowodzony sąd z tej racji w sposób logicznie niezawodny wynika. Wykazanie tego procesu wynikania jest traktowane jako wystarczająca podstawa uznania prawdziwości dowodzonego sądu.
W logice wyróżnia się dwa zasadnicze rodzaje dowodów.
[(p q) ∧ (q r)] (p r)
Przykład:
Jeżeli Jan jest dyrektorem , to z tego wynika, że Jan jest przełożonym i jeżeli Jan jest przełożonym to wniosek z tego, ze Jan ma uprawnienia dyscyplinarne, to z tego wynika, że Jan jest dyrektorem to ma uprawnienia dyscyplinarne
Jan jest dyrektorem to ma uprawnienia dyscyplinarne.
Prawo sylogizmu hipotetycznego koniunkcyjnego
[(p→q)∧(q→r)]→(p→r)
Oprócz dowodów logicznych wymienia się też niekiedy dowody nie w pełni logiczne. Przykładami takowych dowodów mogą być:
Temat: Logiczna analiza zdań pytających (erotetyka).
W logicznej strukturze każdego pytania możemy wyróżnić takie zasadnicze elementy jak:
Analizując poprawność sformułowanych pytań, analiza ta powinna być przeprowadzana przynajmniej z takich punktów widzenia jak:
Dane pytanie określimy jako logicznie poprawne wtedy, kiedy spełnia takie warunki jak:
Logika
Wykład XVII
Ze względu na logiczną strukturę danego pytania, pytania dzielimy na:
Logiczna rozstrzygalność danego pytania polega na tym, że pytanie to powinno spełniać tak zwane formalne założenia, takie jak:
Przyjęcie powyższych założeń jest jednym z najistotniejszych czynników przeciwdziałających formułowaniu tak zwanych pytań wszechogarniających, pytań z tak zwaną strategią dyktatorską, pytań nadmiernie sugerujących, czy nawet pytań obraźliwych.
Pytaniami wszechogarniającymi nazywamy takie pytania, które bądź ze względu na istotę zjawiska, do którego kierowane jest to pytanie, bądź ze względu na formy pytania pozwala na to, że każda z możliwych odpowiedzi może być traktowana jako prawdziwa jak i fałszywa.
Pytaniami ze strategią dyktatorską nazywamy takie pytania, które już na mocy treści pytania zakładają, że może być tylko jedna poprawnie pozytywna odpowiedź.
Pytaniami nadmiernie sugerującymi, lub nawet obraźliwymi nazywamy takie pytania, w których używane są wyrażenia o wysokim stopniu emocjonalności, przez co treść tych pytań wyraźnie sugeruje możliwą odpowiedź.
Merytoryczna analiza pytań polegać będzie przede wszystkim na określeniu rodzaju związku przedmiotowego treści danego pytania z rodzajem rzeczywistości do której pytanie to się odnosi, oraz z możliwością określenia sposobów postępowania, które należy zrealizować, by uzyskać na to pytanie poprawną odpowiedź.
Ze względu na merytoryczną analizę pytania zazwyczaj rozróżnia się według takich kryteriów jak:
Prakseologiczna ocena poprawności pytań powinna dotyczyć przede wszystkim:
Logika
Wykład XIX
Temat: Logiczna teoria argumentacji (przekonywania)
Przekonywaniem nazywamy zazwyczaj proces, którego zasadniczym celem jest wystąpienie tak zwanej postawy akceptującej odnośnie danych poglądów, sądów, działań itp. U poszczególnych ludzi lub też u siebie samego. Właśnie ze względu na konieczność wystąpienia owej postawy akceptującej proces przekonywania jest zróżnicowany i może przebiegać od postaw w pełni wątpiących do postaw w pełni akceptujących, które w skrajnych przypadkach mogą mieć nawet postać postaw fanatycznych.
W procesie przekonywania mogą wystąpić zarówno elementy o charakterze logicznym (racjonalnym) jak i elementy o charakterze pozalogicznym (np.: emocjonalnym, psychologicznym, socjologicznym itp.). Niezależnie jednak od charakteru i zakresu procesów przekonywania można wyróżnić występujące w nim najczęściej dwa zasadnicze elementy.
Najczęstszym sposobem przekonywania powinna być tak zwana rzeczowa dyskusja. Zgodnie z koncepcją Tadeusza Kotarbińskiego przez dyskusję rozumieć należy zbiorowe, uporządkowane wypowiadanie swoich przeglądów odnośnie przyjętego przedmiotu dyskusji w celu wypracowania poprawnej odpowiedzi na dane pytanie uzyskać rozstrzygnięcie wątpliwego sadu, czy wreszcie rozwiązać nurtujący nas problem. Rzeczowa dyskusja powinna więc spełniać takie warunki jak:
INDUKCJA
Niezupełna
Zupełna
Eliminacyjna
Enumeracyjna
nadrzędność
podrzędność
nadrzędność
podrzędność
Wyszukiwarka
Podobne podstrony:
Metodologia badań z logiką dr Karyłowski wykład 7 Testowalna w sposób etycznie akceptowalny
logika wyklad 02
LOGIKA wyklad 5 id 272234 Nieznany
Analiza Wyklad 01 Logika id 59757 (2)
logika wyklad 07
Logika wykład II - 20.10.2013, Sem. 1, Logika
Prawo rzymskie - prawo osobowe, prawoznawstwo, polskie prawo konstytucyjne, Logika i wykładnia prawa
Logika wykłady
logika wyklad 01
Logika wyklad 7
Logika wyklad 1
WYKŁAD 7, LOGIKA
LOGIKA 16.10.2010 - wyklad 1, Logika
Logika wykłady
Wykład z dnia 10.05.2008, Zajęcia, II semestr 2008, Matematyka dyskretna i logika
l. wykład 12, logika
więcej podobnych podstron