7.3. Równania paraboliczne

Zajmiemy się najpierw rozwiązywaniem najprostszego zagadnienia dla równania dyfuzji z jedną zmienną przestrzenną (7.15), polegającego na wyznaczeniu funkcji spełniającej wewnątrz prostokąta

równanie (7.15), warunek początkowy

(7.32)

i warunki brzegowe:

(7.33)

Zagadnienie to będziemy rozwiązywać na siatce czasowo-przestrzennej, określonej krokiem czasowym Δ t i krokiem przestrzennym h.

Metoda jawna pierwszego rzędu. Po zastąpieniu pochodnej ilorazem różnicowym (5.4) oraz pochodnej ilorazem różnicowym (5.15) otrzymamy schemat różnicowy

pierwszego rzędu z błędem aproksymacji
który przepiszemy w postaci

(7.34)

gdzie

(7.35)

Sposób wykonywania obliczeń za pomocą tego schematu całkowania jest przed-stawiony na rysunku 7.1. Druga pochodna przestrzenna jest wyznaczana za pomocą wartości funkcji w trzech punktach:
Pochodna względem czasu jest obliczana między punktami

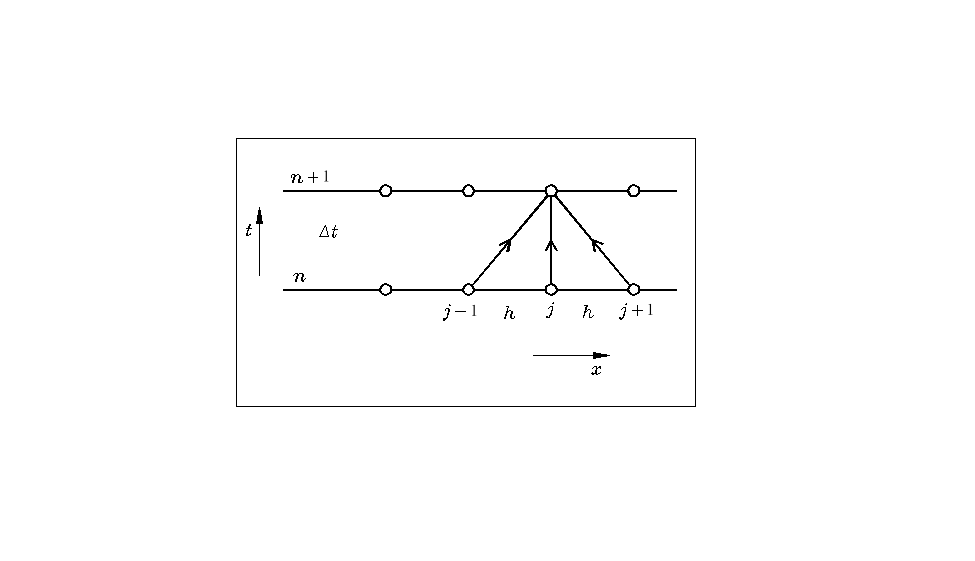
Rys. 7.1

Wprowadzając do schematu różnicowego (7.34) aktualnie wyznaczane rozwiązanie numeryczne, przedstawione w postaci sumy rozwiązania dokładnego tego równania różnicowego U i błędów zaokrągleń

stwierdzamy, że błędy zaokrągleń muszą spełniać ten sam schemat różnicowy co rozwiązanie dokładne.

Dla zbadania stabilności schematu różnicowego (7.34) podstawimy do niego fun-kcję (7.28)

i stąd po wykorzystaniu wzoru

oraz zależności (7.29) otrzymujemy

(7.36)

gdzie

(7.37)

Z kryterium stabilności von Neumanna (7.30) wynika nierówność

- co oznacza, że dla dowolnej liczby falowej k krok czasowy musi być ograniczony

(7.38)

Dla otrzymania stabilnego rozwiązania numerycznego należy zatem wybrać krok czasowy mniejszy od kroku (7.38). Maksymalny dopuszczalny krok czasowy jest po prostu czasem dyfuzji (7.21) związanym z krokiem siatki h i z prędkością rozchodzenia się informacji po siatce, która może być zbyt mała w związku ze zbyt dużym krokiem czasowym.

Metoda niejawna pierwszego rzędu (metoda Laasonena). Schemat różnicowy w tej metodzie otrzymujemy aproksymując pochodną przestrzenną na warstwie czasowej

.

Po zapisaniu tego schematu w postaci

(7.39)

wyznaczamy współczynnik wzmocnienia

(7.40)

Metoda jest bezwarunkowo stabilna, gdyż

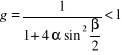
niezależnie od długości kroku czasowego.

Kosztem uzyskania bezwarunkowej stabilności schematu (7.39) jest konieczność rozwiązywania na każdej warstwie czasowej
układu równań z trójdiagonalną macierzą współczynników - rys. 7.2.

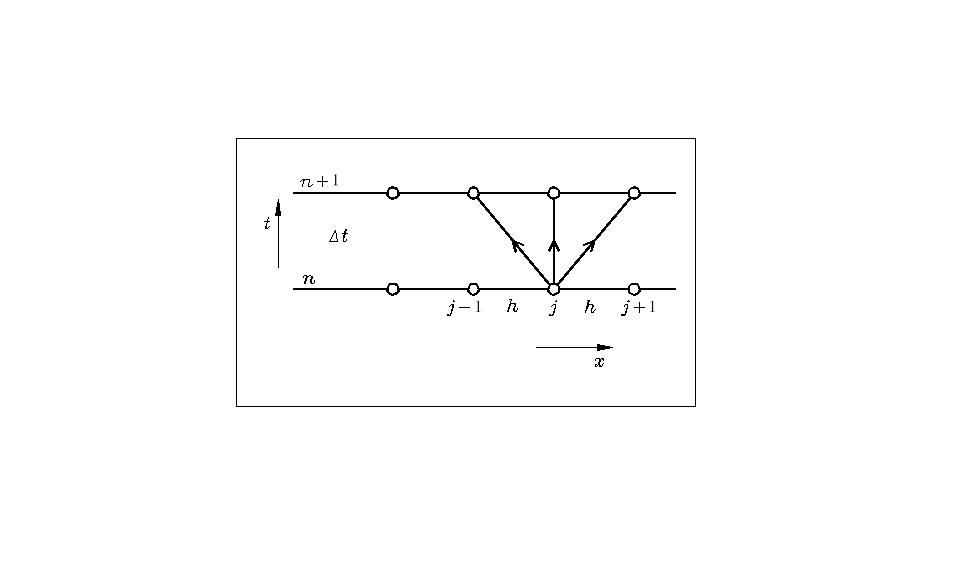
Rys. 7.2

Metoda Cranka-Nicolsona. W metodzie Cranka-Nicolsona uśredniany jest w czasie człon dyfuzji przestrzennej, co formalnie polega na dodaniu do siebie stronami wzorów (7.34) i (7.39)

(7.41)

Analizując stabilność schematu (7.41) stwierdzamy, że współczynnik wzmocnienia

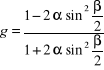
(7.42)

jest dla wszystkich liczb falowych oraz dla dowolnych kroków czasowych liczbą rzeczywistą zawsze mniejszą od jedności. Metoda Cranka-Nicolsona jest więc bezwzględnie stabilna. Ponadto ma ona dokładność drugiego rzędu ze względu zarówno na krok czasowy, jak i na krok przestrzenny. Podobnie jak w schemacie (7.39) dokładność i stabilność została uzyskana kosztem bardziej złożonego układu równań na określenie zmiennych dla wszystkich

Dokładność drugiego rzędu schematu Cranka-Nicolsona ze względu na krok czasowy wynika z rozwinięć oraz
w szeregi Taylora:

Ostatecznie po pominięciu wskaźników j oraz n otrzymamy

Metoda Duforta-Frankela. Narzucającym się sposobem aproksymacji pochodnej czasowej jest jej zastąpienie centralnym ilorazem różnicowym (5.6)

Otrzymany schemat różnicowy (schemat Richardsona)

(7.43)

jest jednakże bezwzględnie niestabilny. Analizując bowiem stabilność tego schematu uzyskujemy równanie

z którego wynika, że jeden ze współczynników wzmocnienia

jest zawsze mniejszy od jedności.

Schemat metody Duforta-Frankela jest modyfikacją schematu (7.43)

(7.44 a)

Zmienna zależna stojąca pod znakiem operatora dyfuzji dla punktu centralnego w czasie i w przestrzeni została zastąpiona średnią z poziomów

Rozwiązując równanie (7.44 a) względem otrzymujemy

(7.44 b)

Dla tego trzypoziomowego wzoru równanie na współczynnik wzmocnienia jest równaniem kwadratowym

którego pierwiastki są następujące:

Aby ocenić wielkości wyznaczonych współczynników wzmocnienia rozważymy dwa przypadki:

1) 
Współczynniki wzmocnienia są rzeczywiste, a ich moduły nie większe od jedności

gdzie

2)  W tym przypadku współczynniki wzmocnienia są zespolone o module

Metoda Duforta-Frankela jest metodą bardzo skuteczną, gdyż jest równocześnie metodą jawną i stabilną. Należy przy tym zauważyć, że dla dużych kroków czasowych współczynnik wzmocnienia jest zespolony - skąd wynika, że w granicy dużych kroków czasowych może ona prowadzić do niewzrastających oscylacji.

Rozwijając, podobnie jak w przypadku schematu Cranka-Nicolsona, występujące we wzorze (7.44a) wielkości oraz w szeregi Taylora dostaniemy równanie określające błąd aproksymacji

(7.45)

który zależy przede wszystkim od ilorazu Przy → 0 i h → 0 człon zawierający może dążyć do jakiejś liczby ≠ 0; musi więc być dodatkowo spełniony warunek, aby → 0. Powyższy przykład jest ilustracją potrzeby zastrzeżenia o zgodności schematu zawartego w twierdzeniu Laxa.

*

Uogólnienie wszystkich opisanych metod różnicowych dla wielowymiarowego równania dyfuzji nie nastręcza zasadniczo większych trudności. Jednak zastosowanie takich uogólnionych schematów różnicowych napotyka na pewne problemy obliczeniowe, które prześledzimy na przykładzie rozwiązywania dwuwymiarowego równania dyfuzji

(7.46)

za pomocą jawnej i niejawnej metody pierwszego rzędu.

Metoda jawna pierwszego rzędu. Po uogólnieniu schematu (7.34) dla otrzymujemy

(7.47)

Dla przeanalizowania stabilności tego schematu rozważymy dwuwymiarowy mod Fouriera

(7.48)

Korzystając z równania różnicowego dostajemy

(7.49)

gdzie:

(7.50)

i następnie z warunku (7.30) wynika ograniczenie na krok czasowy

(7.51)

W porównaniu z warunkiem (7.38) dla jednowymiarowego równania dyfuzji otrzymaliśmy dwukrotne zmniejszenie dopuszczalnego kroku czasowego.

Metoda niejawna pierwszego rzędu. Wynikiem uogólnienia schematu (7.39) dla równania (7.46) jest wzór

(7.52)

Po podstawieniu do tego wzoru modu (7.48) uzyskujemy zależność

(7.53)

z której wynika, że metoda jest bezwarunkowo stabilna

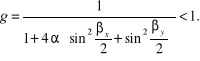
(7.54)

Jednakże układ (7.52) nie jest już układem równań z trójdiagonalną macierzą współczynników, gdyż zawiera pięć kolejnych niewiadomych: Układ ten przepiszemy w postaci

(7.55)

438 7. Równania różniczkowe cząstkowe

7.3. Równania paraboliczne 439

---