16 1.3963E+0000 1.083999259E+0000 2.8723E-0003

17 1.4835E+0000 1.096533117E+0000 2.9055E-0003

18 1.5708E+0000 1.100721695E+0000 2.9166E-0003

19 1.6581E+0000 1.096533117E+0000 2.9055E-0003

20 1.7453E+0000 1.083999259E+0000 2.8723E-0003

21 1.8326E+0000 1.063215513E+0000 2.8172E-0003

22 1.9199E+0000 1.034340055E+0000 2.7407E-0003

23 2.0071E+0000 9.975926439E-0001 2.6434E-0003

24 2.0944E+0000 9.532529507E-0001 2.5259E-0003

25 2.1817E+0000 9.016584269E-0001 2.3892E-0003

26 2.2689E+0000 8.432017381E-0001 2.2343E-0003

27 2.3562E+0000 7.783277750E-0001 2.0624E-0003

28 2.4435E+0000 7.075302675E-0001 1.8748E-0003

29 2.5307E+0000 6.313480274E-0001 1.6729E-0003

30 2.6180E+0000 5.503608477E-0001 1.4583E-0003

31 2.7053E+0000 4.651850895E-0001 1.2326E-0003

32 2.7925E+0000 3.764689920E-0001 9.9755E-0004

33 2.8798E+0000 2.848877381E-0001 7.5488E-0004

34 2.9671E+0000 1.911383165E-0001 5.0647E-0004

35 3.0543E+0000 9.593421692E-0002 2.5420E-0004

36 3.1416E+0000 0.000000000E+0000 -1.0402E-0011

7.4. Równania hiperboliczne

Ograniczymy się do przedstawienia podstawowych schematów różnicowych wykorzystywanych przy rozwiązywaniu jednowymiarowego równania adwekcji oraz możliwości ich uogólnień dla zagadnień opisywanych wielowymiarowymi równaniami adwekcji. Schematy różnicowe dla równania hiperbolicznego (7.13), opisującego rozprzestrzenianie się fali w kierunku osi x ze stałą prędkością c, budować będziemy w podobny sposób jak schematy różnicowe dla równania parabolicznego (7.15) - przyjmując, że siatka jest określona krokiem przestrzennym h i krokiem czasowym

Jawna metoda Eulera. Skonstruujemy schemat różnicowy, analogiczny do sche-matu różnicowego (7.34) dla równania parabolicznego (7.15)

który przepiszemy w postaci

(7.62)

zawierającej bezwymiarową wielkość

(7.63)

nazywaną liczbą Couranta.

Rozważając wzmocnienie modu Fouriera (7.28)

wyznaczamy współczynnik wzmocnienia

(7.64)

gdzie jest oznaczeniem (7.37). Moduł otrzymanego współczynnika wzmocnienia

jest zawsze większy od jedności. Schemat różnicowy (7.62) jest zatem wewnętrznie niestabilny dla wszystkich - co świadczy o tym, że nie wszystkie zgodne i narzucające się schematy są użyteczne.

Metoda Laxa. Stabilny i użyteczny schemat pierwszego rzędu dokładności można uzyskać po zastąpieniu w algorytmie jawnej metody Eulera (7.62) średnią w przestrzeni

(7.65)

Schemat ten, znany jako schemat Laxa, jest szeroko stosowany przy rozwiązywaniu równań hiperbolicznych.

Analizując stabilność schematu Laxa (7.65) stwierdzamy, że współczynnik wzmocnienia jest dany wzorem

(7.66)

Współczynnik ten ma amplitudę

Warunek stabilności von Neumanna będzie spełniony dla wszystkich liczb falowych k, dla których

i stąd otrzymamy warunek stabilności nakładany na krok czasowy

(7.67)

Warunek (7.67) jest szczególnym przypadkiem ogólnego warunku CourantaFriedrichsa-Lewy'ego, odnoszącego się do równań hiperbolicznych [11]. Korzystanie z metody jawnej wymaga wybrania takiego kroku czasowego, który zapewnia przenoszenie się rozwiązania numerycznego z prędkością większą od prędkości fizycznej c.

W celu zilustrowania własności dysypacji i dyspersji schematu Laxa (7.65) wy-prowadzimy dla niego związek dyspersyjny (7.31). Rozważając mod Fouriera (7.16) mamy

i następnie po skróceniu wspólnych czynników dostajemy

(7.68)

W ogólności częstość jest zespolona. Zapisując ją w postaci możemy w otrzymanym związku dyspersyjnym porównać części rzeczywiste i urojone:

Stąd wyznaczamy

(7.69)

oraz

(7.70)

Z zależności (7.70) wynika, że w szczególnym przypadku gdy wtedy część urojona τ równa się zeru i związek dyspersyjny zgadza się dokładnie ze związkiem dyspersyjnym dla równania różniczkowego (7.13). W przypadku ogólnym jest jednak co wiąże się z występowaniem na siatce dysypacji i dyspersji.

Przy wykorzystaniu rozwiązania dokładnego równania (7.13)

możemy obliczyć dokładną wartość współczynnika wzmocnienia

(7.71)

i porównać ją z wartością przybliżoną (7.66). W rezultacie otrzymujemy:

dysypacja

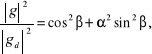
(7.72)

dyspersja

(7.73)

gdzie i
są kątami fazowymi: przybliżonym i dokładnym.

Rys. 7.5

Widać, że zarówno dysypacja jak i dyspersja zależą od liczby Couranta oraz Dla dużych liczb falowych k (dla małych długości fal) efekty dysypacji i dyspersji mogą być znaczne i mogą one powodować powstawanie dużych błędów obliczeń. Wpływ błędów dysypacji i dyspersji na postać rozwiązania jest pokazany na rysunku 7.5.

Metoda „upwind” („pod prąd”). W metodzie tej stabilność schematu (7.62) została uzyskana w wyniku zastąpienia różnicy centralnej różnicą wsteczną

(7.74)

Jest to schemat pierwszego rzędu dokładności z błędem aproksymacji

Po wstawieniu do schematu (7.74) modu Fouriera (7.28) otrzymujemy

i następnie

Schemat jest warunkowo stabilny dla czyli dla kroków czasowych określonych, tak samo jak w metodzie Laxa, nierównością (7.67).

Niejawna metoda pierwszego rzędu. Aproksymując pochodną przestrzenną w równaniu (7.13) centralnym ilorazem różnicowym, wyznaczanym na warstwie czasowej
otrzymujemy

(7.75)

Na każdym kroku czasowym musi być więc rozwiązywany układ równań z trój-diagonalną macierzą współczynników.

Po obliczeniu współczynnika wzmocnienia

stwierdzamy, że schemat (7.75) jest bezwarunkowo stabilny, gdyż

(7.76)

Z postaci wzoru (7.76) wynika, że niejawna metoda pierwszego rzędu charakteryzuje się dużą dysypacją dla średnich wartości liczb falowych. Ponadto również dyspersja

jest duża dla dużych wartości liczb falowych.

Metoda skokowa. Trudności związane z uzyskaniem jawnych stabilnych schematów różnicowych postaci (7.62) dla równania (7.13) wynikały z zastąpienia po-chodnej względem czasu progresywnym ilorazem różnicowym. Trudności te można pokonać stosując metodę drugiego rzędu dokładności w postaci wzoru trójpoziomowego

(7.77)

analogicznego do wzoru schematu Duforta-Frankela (7.43) dla jednowymiarowych równań parabolicznych.

Dla współczynnika wzmocnienia określonego przez dwustopniowy schemat różnicowy (7.77) otrzymujemy równanie kwadratowe

(7.78)

Równanie to ma dwa pierwiastki

, (7.79)

których moduły będą równe jedności w odniesieniu do wszystkich liczb falowych spełniających warunek

czyli dla kroku czasowego określonego zgodnie z nierównością (7.67).

Metoda skokowa oprócz niedogodności związanych z koniecznością zadawania warunków początkowych na dwu poziomach czasowych i większymi wymaganiami odnoszącymi się do pamięci komputera, charakteryzuje się wykonywaniem obliczeń na dwu niesprzężonych siatkach ( nie zależy od ) - rys. 7.6, co może powodować rozprzęganie się rozwiązań odpowiadających tym siatkom.

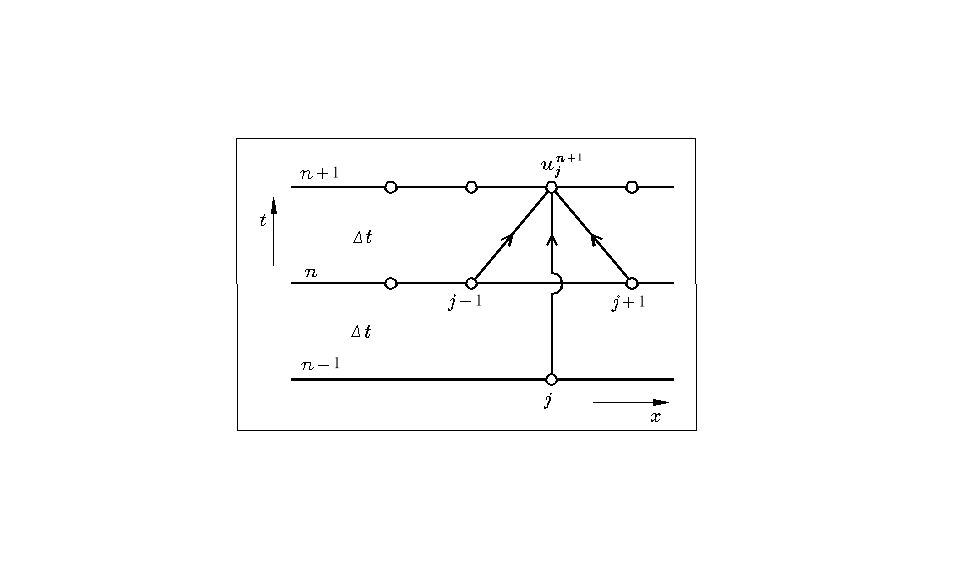
Rys. 7.6

Metoda Laxa-Wendroffa. Schemat różnicowy Laxa-Wendroffa z błędem ap-roksymacji można wyprowadzić z rozwinięcia w szereg Taylora zmiennej względem punktu

(7.80)

przy wykorzystaniu równań falowych - pierwszego i drugiego rzędu:

w których pochodne przestrzenne i zostały zastąpione centralnymi ilorazami różnicowymi drugiego rzędu dokładności

(7.81)

Po wyznaczeniu współczynnika wzmocnienia

(7.82)

i następnie jego modułu

stwierdzamy, że jawny schemat różnicowy (7.81) jest warunkowo stabilny, podobnie jak poprzednio rozważane schematy jawne, jeśli spełniony jest warunek Couranta-Friedrichsa-Lewy'ego (7.67):

Niejawna metoda drugiego rzędu. Odejmując od rozwinięcia (7.80) rozwinięcie w szereg Taylora zmiennej względem punktu

i uwzględniając dodatkowo rozwinięcie dla drugiej pochodnej

otrzymamy wzór następujący

(7.83)

Zastępując w zależności (7.83) pochodne czasowe pochodnymi przestrzennymi i następnie pochodne przestrzenne ich centralnymi ilorazami różnicowymi uzyskamy schemat różnicowy aproksymujący równanie (7.13) z dokładnością

(7.84)

Po wyznaczeniu współczynnika wzmocnienia

(7.85)

stwierdzamy, że jego moduł jest zawsze równy jedności, niezależnie od wartości liczby falowej k. Zatem schemat (7.84) jest bezwzględnie stabilny.

*

Przedstawione jawne schematy różnicowe dla jednego wymiaru w przestrzeni dają się w sposób naturalny rozszerzyć na równania opisujące zagadnienia wielo-wymiarowe i właśnie w takich zagadnieniach metody te znajdują największe zastosowanie.

Możliwość łatwego uogólniania jednowymiarowych schematów różnicowych prześledzimy na przykładzie metody Laxa, zastosowanej do rozwiązywania dwuwymiarowego równania adwekcji

(7.86)

Schemat Laxa dla równania (7.86) przybiera postać następującą

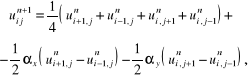
(7.87)

gdzie:

W schemacie tym zmienną zastąpiono średnią w przestrzeni, wziętą z czterech punktów przylegających.

Stosując analizę stabilności von Neumanna dla podwójnego modu (7.48) wyznaczamy współczynnik wzmocnienia

(7.88)

gdzie I jest jednostką urojoną, a i są oznaczeniami (7.50).

Badając moduł współczynnika wzmocnienia (7.88)

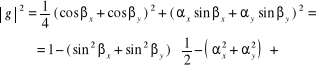
stwierdzamy, że warunek stabilności von Neumanna (7.30) będzie spełniony, jeśli

Stąd wynika ograniczenie na krok czasowy

(7.89)

będące warunkiem Couranta-Friedrichsa-Lewy'ego dla zagadnień dwuwymiarowych.

Warunek Couranta-Friedrichsa-Lewy'ego nakładany na krok czasowy w przypadku N wymiarów przestrzennych przyjmuje postać

, (7.90)

gdzie jest modułem największej prędkości propagacji na siatce.

Również jednowymiarowe schematy niejawne można w podobny sposób rozszerzyć na równanie odnoszące się do zagadnień dwu i trójwymiarowych. Jednakże ze względu na konieczność rozwiązywania dużych układów równań (jak np. równania postaci (7.56)) stosowane są głównie schematy, w których wykorzystywana jest dekompozycja strumieni - co pozwala na zredukowanie dużych układów równań do mniejszych układów równań różnicowych [39, 40].

*

Kolejny z prezentowanych programów komputerowych przeznaczony jest do rozwiązywania równania

z warunkiem początkowym

i okresowymi warunkami brzegowymi. Rozwiązaniem dokładnym tego zagadnienia jest funkcja

Zagadnienie jest rozwiązywane za pomocą wszystkich sześciu omówionych stabilnych metod różnicowych.

Sposób działania programu 7.2 jest taki sam jak sposób działania programu 7.1 - z tą tylko różnicą, że procedura Tridiag1 została zastąpiona procedurą

Tridiag2(n,a,b,c,d,x),

w której rozwiązywany jest układ równań (2.84) za pomocą algorytmu określonego wzorami (2.90) ÷ (2.94).

{Program 7.2}

unit Obliczenia;

interface

uses

Windows, Messages, SysUtils, Classes, Graphics, Controls,

Forms, Dialogs, StdCtrls, Buttons;

type

Tabl = array[0..100] of Real;

. . . . . . . . . . . . . . . .

var

Form3: TForm3;

a,al,b,bl,dt,h,p,t,tmax,x: Real;

aa,bb,cc,dd,u,un,un1: Tabl;

j,m,m1,nr: Integer;

plik: Text;

implementation

uses Ustawienia, Informacje, Grafika, Podglad;

{$R *.DFM}

function u0(x: Real): Real;

begin

u0:=Sin(2*x);

end;

function ud(x,t: Real): Real;

begin

ud:=Sin(2*(x-t));

end;

{procedure Tridiag2(n: Integer; a,b,c,d: Tabl;

var x: Tabl);}

. . . . . . . . . . . . . . . . . . . . . . .

procedure TForm3.BitBtn1Click(Sender: TObject);

begin

Form2.Show;

AssignFile(plik,Edit4.Text);

Rewrite(plik); Writeln(plik,'PROGRAM 7.2.');

Writeln(plik,'Zagadnienie początkowo-brzegowe');

Writeln(plik,'dla równania hiperbolicznego.');

a:=StrToFloat(Edit1.Text);

b:=StrToFloat(Edit2.Text);

m:=StrToInt(Edit3.Text);

dt:=StrToFloat(Edit6.Text);

tmax:=StrToFloat(Edit7.Text);

if RadioButton1.Checked then nr:=1;

if RadioButton2.Checked then nr:=2;

if RadioButton3.Checked then nr:=3;

if RadioButton4.Checked then nr:=4;

if RadioButton5.Checked then nr:=5;

if RadioButton6.Checked then nr:=6;

case nr of

1: Writeln(plik,'Metoda Laxa.');

2: Writeln(plik,'Metoda "upwind".');

3: Writeln(plik,'Metoda niejawna pierwszego rzędu.');

4: Writeln(plik,'Metoda skokowa.');

5: Writeln(plik,'Metoda Laxa-Wendroffa.');

6: Writeln(plik,'Metoda niejawna drugiego rzędu.');

end;

Writeln(plik);

Writeln(plik,'Liczba podprzedziałów: m = ',m:3);

Writeln(plik,'Początek przedziału: a = ',a:13);

Writeln(plik,'Koniec przedziału: b = ',b:13);

Writeln(plik,'Krok czasowy: dt = ',dt:13);

Writeln(plik); h:=(b-a)/m; al:=dt/h;

for j:=0 to m do begin

x:=a+j*h;

un[j]:=u0(x);

end;

t:=0; m1:=m+1;

un[m1]:=un[1];

repeat

t:=t+dt;

case nr of

1: for j:=1 to m do begin

p:=al*(un[j+1]-un[j-1])/2;

u[j]:=(un[j-1]+un[j+1])/2-p;

end;

2: for j:=1 to m do

u[j]:=un[j]-al*(un[j]-un[j-1]);

3: begin

for j:=1 to m do begin

aa[j]:=-al/2; bb[j]:=1;

cc[j]:=al/2; dd[j]:=un[j];

end;

Tridiag2(m,aa,bb,cc,dd,u);

end;

4: if Abs(t-dt)<1e-10 then

for j:=1 to m do

u[j]:=ud(a+j*h,t)

else

for j:=1 to m do begin

p:=un[j+1]-un[j-1];

u[j]:=un1[j]-al*p;

end;

5: for j:=1 to m do begin

p:=al*al*(un[j-1]-2*un[j]+un[j+1])/2;

u[j]:=un[j]-al*(un[j+1]-un[j-1])/2+p;

end;

6: begin

for j:=1 to m do begin

aa[j]:=-al/4;

bb[j]:=1;

cc[j]:=al/4;

p:=un[j+1]-un[j-1];

dd[j]:=un[j]-al*p/4;

end;

Tridiag2(m,aa,bb,cc,dd,u);

end;

end;

u[0]:=u[m]; u[m1]:=u[1];

for j:=0 to m1 do begin

un1[j]:=un[j];

un[j]:=u[j];

end;

until (t>=tmax);

Writeln(plik,'Wartości funkcji u(x,t) dla t = ',t:13,':');

Writeln(plik,' j x[j] u[j] błąd');

for j:=0 to m do begin

x:=a+j*h; bl:=ud(x,t)-u[j];

Writeln(plik,j:3,' ',x:13,' ',u[j]:18,' ',bl:13);

end;

Writeln(plik); CloseFile(plik);

Form2.Wyniki.Lines.LoadFromFile(Edit4.Text);

end;

. . . . . . . . . . . . . . . . . . . . . . .

procedure TForm3.BitBtn3Click(Sender: TObject);

begin

Close;

end;

end.

Załączone wydruki komputerowe zawierają wyniki obliczeń numerycznych otrzymane przy wykorzystaniu wszystkich schematów różnicowych dla przy-jęto oraz Wyniki te pozwalają na przeana-lizowanie własności poszczególnych schematów różnicowych, a w szczególności dysypacji, której efekty najbardziej są widoczne w przypadku metody Laxa.

PROGRAM 7.2.

Zagadnienie początkowo-brzegowe

dla równania hiperbolicznego.

Metoda Laxa.

Liczba podprzedziałów: m = 36

Początek przedziału: a = 0.0000E+0000

Koniec przedziału: b = 3.1416E+0000

Krok czasowy: dt = 5.0000E-0002

Wartości funkcji u(x,t) dla t = 1.0000E+0000:

j x[j] u[j] błąd

0 0.0000E+0000 -7.363080188E-0001 -1.7299E-0001

1 8.7266E-0002 -7.857733631E-0001 -1.8197E-0001

2 1.7453E-0001 -8.113633814E-0001 -1.8543E-0001

3 2.6180E-0001 -8.123005339E-0001 -1.8325E-0001

4 3.4907E-0001 -7.885563457E-0001 -1.7550E-0001

5 4.3633E-0001 -7.408522720E-0001 -1.6242E-0001

6 5.2360E-0001 -6.706377769E-0001 -1.4440E-0001

7 6.1087E-0001 -5.800462923E-0001 -1.2200E-0001

8 6.9813E-0001 -4.718303946E-0001 -9.5892E-0002

9 7.8540E-0001 -3.492781692E-0001 -6.6869E-0002

10 8.7266E-0001 -2.161133033E-0001 -3.5813E-0002

11 9.5993E-0001 -7.638194402E-0002 -3.6701E-0003

12 1.0472E+0000 6.567024194E-0002 2.8585E-0002

13 1.1345E+0000 2.057270708E-0001 5.9971E-0002

14 1.2217E+0000 3.395329868E-0001 8.9535E-0002

15 1.3090E+0000 4.630223647E-0001 1.1637E-0001

16 1.3963E+0000 5.724430424E-0001 1.3969E-0001

17 1.4835E+0000 6.644703280E-0001 1.5875E-0001

18 1.5708E+0000 7.363080188E-0001 1.7299E-0001

19 1.6581E+0000 7.857733631E-0001 1.8197E-0001

20 1.7453E+0000 8.113633814E-0001 1.8543E-0001

21 1.8326E+0000 8.123005339E-0001 1.8325E-0001

22 1.9199E+0000 7.885563457E-0001 1.7550E-0001

23 2.0071E+0000 7.408522720E-0001 1.6242E-0001

24 2.0944E+0000 6.706377769E-0001 1.4440E-0001

25 2.1817E+0000 5.800462923E-0001 1.2200E-0001

26 2.2689E+0000 4.718303946E-0001 9.5892E-0002

27 2.3562E+0000 3.492781692E-0001 6.6869E-0002

28 2.4435E+0000 2.161133033E-0001 3.5813E-0002

29 2.5307E+0000 7.638194403E-0002 3.6701E-0003

30 2.6180E+0000 -6.567024194E-0002 -2.8585E-0002

31 2.7053E+0000 -2.057270708E-0001 -5.9971E-0002

32 2.7925E+0000 -3.395329868E-0001 -8.9535E-0002

33 2.8798E+0000 -4.630223647E-0001 -1.1637E-0001

34 2.9671E+0000 -5.724430424E-0001 -1.3969E-0001

35 3.0543E+0000 -6.644703280E-0001 -1.5875E-0001

36 3.1416E+0000 -7.363080188E-0001 -1.7299E-0001

PROGRAM 7.2.

Zagadnienie początkowo-brzegowe

dla równania hiperbolicznego.

Metoda "upwind".

Liczba podprzedziałów: m = 36

Początek przedziału: a = 0.0000E+0000

Koniec przedziału: b = 3.1416E+0000

Krok czasowy: dt = 5.0000E-0002

Wartości funkcji u(x,t) dla t = 1.0000E+0000:

j x[j] u[j] błąd

0 0.0000E+0000 -8.436687425E-0001 -6.5629E-0002

1 8.7266E-0002 -8.980115271E-0001 -6.9735E-0002

2 1.7453E-0001 -9.250686858E-0001 -7.1722E-0002

3 2.6180E-0001 -9.240181007E-0001 -7.1530E-0002

4 3.4907E-0001 -8.948916931E-0001 -6.9165E-0002

5 4.3633E-0001 -8.385744543E-0001 -6.4698E-0002

6 5.2360E-0001 -7.567775550E-0001 -5.8265E-0002

7 6.1087E-0001 -6.519863527E-0001 -5.0062E-0002

8 6.9813E-0001 -5.273848750E-0001 -4.0338E-0002

9 7.8540E-0001 -3.867590747E-0001 -2.9388E-0002

10 8.7266E-0001 -2.343817956E-0001 -1.7545E-0002

11 9.5993E-0001 -7.488294429E-0002 -5.1691E-0003

12 1.0472E+0000 8.689118740E-0002 7.3638E-0003

13 1.1345E+0000 2.460251743E-0001 1.9673E-0002

14 1.2217E+0000 3.976838108E-0001 3.1384E-0002

15 1.3090E+0000 5.372590260E-0001 4.2142E-0002

16 1.3963E+0000 6.605098975E-0001 5.1620E-0002

17 1.4835E+0000 7.636915100E-0001 5.9529E-0002

18 1.5708E+0000 8.436687425E-0001 6.5629E-0002

19 1.6581E+0000 8.980115271E-0001 6.9735E-0002

20 1.7453E+0000 9.250686858E-0001 7.1722E-0002

21 1.8326E+0000 9.240181007E-0001 7.1530E-0002

22 1.9199E+0000 8.948916931E-0001 6.9165E-0002

23 2.0071E+0000 8.385744543E-0001 6.4698E-0002

24 2.0944E+0000 7.567775551E-0001 5.8265E-0002

25 2.1817E+0000 6.519863527E-0001 5.0062E-0002

26 2.2689E+0000 5.273848750E-0001 4.0338E-0002

27 2.3562E+0000 3.867590747E-0001 2.9388E-0002

28 2.4435E+0000 2.343817956E-0001 1.7545E-0002

29 2.5307E+0000 7.488294429E-0002 5.1691E-0003

30 2.6180E+0000 -8.689118741E-0002 -7.3638E-0003

31 2.7053E+0000 -2.460251743E-0001 -1.9673E-0002

32 2.7925E+0000 -3.976838109E-0001 -3.1384E-0002

33 2.8798E+0000 -5.372590260E-0001 -4.2142E-0002

34 2.9671E+0000 -6.605098975E-0001 -5.1620E-0002

35 3.0543E+0000 -7.636915100E-0001 -5.9529E-0002

36 3.1416E+0000 -8.436687425E-0001 -6.5629E-0002

PROGRAM 7.2.

Zagadnienie początkowo-brzegowe

dla równania hiperbolicznego.

Metoda niejawna pierwszego rzędu.

Liczba podprzedziałów: m = 36

Początek przedziału: a = 0.0000E+0000

Koniec przedziału: b = 3.1416E+0000

Krok czasowy: dt = 5.0000E-0002

Wartości funkcji u(x,t) dla t = 1.0000E+0000:

j x[j] u[j] błąd

0 0.0000E+0000 -8.301697849E-0001 -7.9128E-0002

1 8.7266E-0002 -8.806484673E-0001 -8.7098E-0002

2 1.7453E-0001 -9.043690917E-0001 -9.2422E-0002

3 2.6180E-0001 -9.006109189E-0001 -9.4937E-0002

4 3.4907E-0001 -8.694881390E-0001 -9.4568E-0002

5 4.3633E-0001 -8.119464020E-0001 -9.1326E-0002

6 5.2360E-0001 -7.297340845E-0001 -8.5308E-0002

7 6.1087E-0001 -6.253491660E-0001 -7.6699E-0002

8 6.9813E-0001 -5.019633296E-0001 -6.5759E-0002

9 7.8540E-0001 -3.633255914E-0001 -5.2821E-0002

10 8.7266E-0001 -2.136483890E-0001 -3.8278E-0002

11 9.5993E-0001 -5.747958840E-0002 -2.2572E-0002

12 1.0472E+0000 1.004357004E-0001 -6.1807E-0003

13 1.1345E+0000 2.552993013E-0001 1.0398E-0002

14 1.2217E+0000 4.024057621E-0001 2.6662E-0002

15 1.3090E+0000 5.372853275E-0001 4.2116E-0002

16 1.3963E+0000 6.558397500E-0001 5.6290E-0002

17 1.4835E+0000 7.544668136E-0001 6.8753E-0002

18 1.5708E+0000 8.301697849E-0001 7.9128E-0002

19 1.6581E+0000 8.806484673E-0001 8.7098E-0002

20 1.7453E+0000 9.043690917E-0001 9.2422E-0002

21 1.8326E+0000 9.006109189E-0001 9.4937E-0002

22 1.9199E+0000 8.694881390E-0001 9.4568E-0002

23 2.0071E+0000 8.119464020E-0001 9.1326E-0002

24 2.0944E+0000 7.297340845E-0001 8.5308E-0002

25 2.1817E+0000 6.253491660E-0001 7.6699E-0002

26 2.2689E+0000 5.019633296E-0001 6.5759E-0002

27 2.3562E+0000 3.633255914E-0001 5.2821E-0002

28 2.4435E+0000 2.136483890E-0001 3.8278E-0002

29 2.5307E+0000 5.747958840E-0002 2.2572E-0002

30 2.6180E+0000 -1.004357004E-0001 6.1807E-0003

31 2.7053E+0000 -2.552993013E-0001 -1.0398E-0002

32 2.7925E+0000 -4.024057621E-0001 -2.6662E-0002

33 2.8798E+0000 -5.372853275E-0001 -4.2116E-0002

34 2.9671E+0000 -6.558397500E-0001 -5.6290E-0002

35 3.0543E+0000 -7.544668136E-0001 -6.8753E-0002

36 3.1416E+0000 -8.301697849E-0001 -7.9128E-0002

PROGRAM 7.2.

Zagadnienie początkowo-brzegowe

dla równania hiperbolicznego.

Metoda skokowa.

Liczba podprzedziałów: m = 36

Początek przedziału: a = 0.0000E+0000

Koniec przedziału: b = 3.1416E+0000

Krok czasowy: dt = 5.0000E-0002

Wartości funkcji u(x,t) dla t = 1.0000E+0000:

j x[j] u[j] błąd

0 0.0000E+0000 -9.120916788E-0001 2.7943E-0003

1 8.7266E-0002 -9.694704331E-0001 1.7241E-0003

2 1.7453E-0001 -9.973923188E-0001 6.0164E-0004

3 2.6180E-0001 -9.950089436E-0001 -5.3915E-0004

4 3.4907E-0001 -9.623927252E-0001 -1.6635E-0003

5 4.3633E-0001 -9.005346908E-0001 -2.7374E-0003

6 5.2360E-0001 -8.113143655E-0001 -3.7281E-0003

7 6.1087E-0001 -6.974426637E-0001 -4.6055E-0003

8 6.9813E-0001 -5.623795196E-0001 -5.3430E-0003

9 7.8540E-0001 -4.102287583E-0001 -5.9181E-0003

10 8.7266E-0001 -2.456134038E-0001 -6.3134E-0003

11 9.5993E-0001 -7.353521030E-0002 -6.5169E-0003

12 1.0472E+0000 1.007773133E-0001 -6.5223E-0003

13 1.1345E+0000 2.720277693E-0001 -6.3296E-0003

14 1.2217E+0000 4.350127992E-0001 -5.9446E-0003

15 1.3090E+0000 5.847801853E-0001 -5.3789E-0003

16 1.3963E+0000 7.167793214E-0001 -4.6498E-0003

17 1.4835E+0000 8.269994804E-0001 -3.7795E-0003

18 1.5708E+0000 9.120916788E-0001 -2.7943E-0003

19 1.6581E+0000 9.694704331E-0001 -1.7241E-0003

20 1.7453E+0000 9.973923188E-0001 -6.0164E-0004

21 1.8326E+0000 9.950089436E-0001 5.3915E-0004

22 1.9199E+0000 9.623927252E-0001 1.6635E-0003

23 2.0071E+0000 9.005346908E-0001 2.7374E-0003

24 2.0944E+0000 8.113143655E-0001 3.7281E-0003

25 2.1817E+0000 6.974426637E-0001 4.6055E-0003

26 2.2689E+0000 5.623795196E-0001 5.3430E-0003

27 2.3562E+0000 4.102287583E-0001 5.9181E-0003

28 2.4435E+0000 2.456134038E-0001 6.3134E-0003

29 2.5307E+0000 7.353521030E-0002 6.5169E-0003

30 2.6180E+0000 -1.007773133E-0001 6.5223E-0003

31 2.7053E+0000 -2.720277693E-0001 6.3296E-0003

32 2.7925E+0000 -4.350127992E-0001 5.9446E-0003

33 2.8798E+0000 -5.847801853E-0001 5.3789E-0003

34 2.9671E+0000 -7.167793214E-0001 4.6498E-0003

35 3.0543E+0000 -8.269994805E-0001 3.7795E-0003

36 3.1416E+0000 -9.120916788E-0001 2.7943E-0003

PROGRAM 7.2.

Zagadnienie początkowo-brzegowe

dla równania hiperbolicznego.

Metoda Laxa-Wendroffa.

. . . . . . . . . . . . . . . . . . .

Wartości funkcji u(x,t) dla t = 1.0000E+0000:

j x[j] u[j] błąd

0 0.0000E+0000 -9.116379545E-0001 2.3405E-0003

1 8.7266E-0002 -9.689412641E-0001 1.1949E-0003

2 1.7453E-0001 -9.968037836E-0001 1.3100E-0005

3 2.6180E-0001 -9.943789245E-0001 -1.1691E-0003

4 3.4907E-0001 -9.617403651E-0001 -2.3159E-0003

5 4.3633E-0001 -8.998798113E-0001 -3.3923E-0003

6 5.2360E-0001 -8.106768648E-0001 -4.3656E-0003

7 6.1087E-0001 -6.968419119E-0001 -5.2062E-0003

8 6.9813E-0001 -5.618337702E-0001 -5.8887E-0003

9 7.8540E-0001 -4.097545937E-0001 -6.3922E-0003

10 8.7266E-0001 -2.452252312E-0001 -6.7016E-0003

11 9.5993E-0001 -7.324482419E-0002 -6.8073E-0003

12 1.0472E+0000 1.009610897E-0001 -6.7061E-0003

13 1.1345E+0000 2.720993521E-0001 -6.4012E-0003

14 1.2217E+0000 4.349700133E-0001 -5.9018E-0003

15 1.3090E+0000 5.846243308E-0001 -5.2231E-0003

16 1.3963E+0000 7.165151338E-0001 -4.3857E-0003

17 1.4835E+0000 8.266349871E-0001 -3.4150E-0003

18 1.5708E+0000 9.116379545E-0001 -2.3405E-0003

19 1.6581E+0000 9.689412641E-0001 -1.1949E-0003

20 1.7453E+0000 9.968037836E-0001 -1.3100E-0005

21 1.8326E+0000 9.943789245E-0001 1.1691E-0003

22 1.9199E+0000 9.617403651E-0001 2.3159E-0003

23 2.0071E+0000 8.998798113E-0001 3.3923E-0003

24 2.0944E+0000 8.106768648E-0001 4.3656E-0003

25 2.1817E+0000 6.968419119E-0001 5.2062E-0003

26 2.2689E+0000 5.618337702E-0001 5.8887E-0003

27 2.3562E+0000 4.097545937E-0001 6.3922E-0003

28 2.4435E+0000 2.452252312E-0001 6.7016E-0003

29 2.5307E+0000 7.324482419E-0002 6.8073E-0003

30 2.6180E+0000 -1.009610897E-0001 6.7061E-0003

31 2.7053E+0000 -2.720993521E-0001 6.4012E-0003

32 2.7925E+0000 -4.349700133E-0001 5.9018E-0003

33 2.8798E+0000 -5.846243308E-0001 5.2231E-0003

34 2.9671E+0000 -7.165151338E-0001 4.3857E-0003

35 3.0543E+0000 -8.266349871E-0001 3.4150E-0003

36 3.1416E+0000 -9.116379545E-0001 2.3405E-0003

PROGRAM 7.2.

Zagadnienie początkowo-brzegowe

dla równania hiperbolicznego.

Metoda niejawna drugiego rzędu.

. . . . . . . . . . . . . . . . . . .

Wartości funkcji u(x,t) dla t = 1.0000E+0000:

j x[j] u[j] błąd

0 0.0000E+0000 -9.141354097E-0001 4.8380E-0003

1 8.7266E-0002 -9.706461719E-0001 2.8999E-0003

2 1.7453E-0001 -9.976643413E-0001 8.7366E-0004

3 2.6180E-0001 -9.943689845E-0001 -1.1791E-0003

4 3.4907E-0001 -9.608602293E-0001 -3.1960E-0003

5 4.3633E-0001 -8.981562223E-0001 -5.1159E-0003

6 5.2360E-0001 -8.081621929E-0001 -6.8803E-0003

7 6.1087E-0001 -6.936125643E-0001 -8.4356E-0003

8 6.9813E-0001 -5.579878689E-0001 -9.7346E-0003

9 7.8540E-0001 -4.054089944E-0001 -1.0737E-0002

10 8.7266E-0001 -2.405119728E-0001 -1.1414E-0002

11 9.5993E-0001 -6.830711663E-0002 -1.1745E-0002

12 1.0472E+0000 1.059732167E-0001 -1.1718E-0002

13 1.1345E+0000 2.770336075E-0001 -1.1335E-0002

14 1.2217E+0000 4.396764724E-0001 -1.0608E-0002

15 1.3090E+0000 5.889599901E-0001 -9.5587E-0003

16 1.3963E+0000 7.203482565E-0001 -8.2188E-0003

17 1.4835E+0000 8.298491057E-0001 -6.6291E-0003

18 1.5708E+0000 9.141354097E-0001 -4.8380E-0003

19 1.6581E+0000 9.706461719E-0001 -2.8999E-0003

20 1.7453E+0000 9.976643413E-0001 -8.7366E-0004

21 1.8326E+0000 9.943689845E-0001 1.1791E-0003

22 1.9199E+0000 9.608602293E-0001 3.1960E-0003

23 2.0071E+0000 8.981562223E-0001 5.1159E-0003

24 2.0944E+0000 8.081621930E-0001 6.8803E-0003

25 2.1817E+0000 6.936125643E-0001 8.4356E-0003

26 2.2689E+0000 5.579878689E-0001 9.7346E-0003

27 2.3562E+0000 4.054089944E-0001 1.0737E-0002

28 2.4435E+0000 2.405119728E-0001 1.1414E-0002

29 2.5307E+0000 6.830711663E-0002 1.1745E-0002

30 2.6180E+0000 -1.059732167E-0001 1.1718E-0002

31 2.7053E+0000 -2.770336075E-0001 1.1335E-0002

32 2.7925E+0000 -4.396764724E-0001 1.0608E-0002

33 2.8798E+0000 -5.889599901E-0001 9.5587E-0003

34 2.9671E+0000 -7.203482565E-0001 8.2188E-0003

35 3.0543E+0000 -8.298491057E-0001 6.6291E-0003

36 3.1416E+0000 -9.141354097E-0001 4.8380E-0003

466 7. Równania różniczkowe cząstkowe

7.4. Równania hiperboliczne 467

---