Rozdział 5

RÓŻNICZKOWANIE, CAŁKOWANIE
I APROKSYMACJA

5.1. Różniczkowanie numeryczne i aproksymacja pochodnych

Ogólne wzory różniczkowania numerycznego można uzyskać po zróżniczkowaniu wzorów interpolacyjnych lub aproksymacyjnych. Należy jednak przy tym pamiętać, że przybliżone różniczkowanie jest operacją mniej dokładną niż interpolacja i aproksymacja funkcji, gdyż wyznaczenie funkcji
, przybliżającej z zadaną dokładnością funkcję
na odcinku
nie zapewnia jednocześnie bliskości funkcji
i
- rys. 5.1.

Rys. 5.1

Jedne z najdokładniejszych metod różniczkowania numerycznego wynikają z zastosowania funkcji sklejanych, które są zawsze zbieżne do interpolowanych i aproksymowanych funkcji. W celu obliczenia pochodnych
oraz
za pomocą wielomianowych funkcji sklejanych trzeciego stopnia trzeba tylko odpowiednio wykorzystać wzory (4.71), (4.73) i (4.74) - (4.75) lub analogiczne wzory dla innych funkcji sklejanych. Jeżeli wykorzystujemy przedstawienie wielomianowej funkcji sklejanej trzeciego stopnia przez B-funkcje sklejane (4.120), to po zróżniczkowaniu (4.120) otrzymujemy

i problem sprowadza się do obliczania pochodnych B-funkcji sklejanych. Wyższe pochodne funkcji
mogą być obliczone metodą "funkcja sklejana od funkcji sklejanej", np. dla funkcji
interpolującej zadane w węzłach wartości pochodnych
mamy

Dokładność aproksymacji pochodnych obliczonych przy wykorzystaniu funkcji sklejanych trzeciego stopnia określają oszacowania (4.110).

W praktyce największe znaczenie mają wzory pozwalające na wyrażanie pochodnych funkcji
za pomocą znanych wartości tej funkcji w równoodległych punktach

(5.1)

których podstawowym zastosowaniem jest rozwiązywanie zagadnień opisywanych równaniami różniczkowymi. Otrzymane w ten sposób ilorazy różnicowe mogą zawierać różnice skończone progresywne i wsteczne (rozdz. 4.3) lub też centralne różnice skończone:

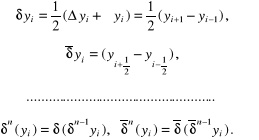
(5.2)

Wzory różnicowe aproksymujące pochodne określonego rzędu w węźle
- zawierające krok siatki (5.1) i wartości funkcji
w węzłach sąsiednich - mogą być wyprowadzane z rozwinięć w szeregi Taylora w połączeniu z metodą mnożników nieoznaczonych drogą różniczkowania wielomianów interpolacyjnych lub też przy wykorzystaniu zależności wynikających z interpolacji funkcjami sklejanymi.

W przypadku najprostszej aproksymacji pierwszej pochodnej, z rozwinięć funkcji
w szeregi Taylora

(5.3)

otrzymujemy następujące wzory:

(5.4)

(5.5)

(5.6)

W pierwszym z tych wzorów występuje progresywna różnica skończona
, w drugim - wsteczna różnica skończona
, a w trzecim różnica centralna (5.2). W pierwszych dwóch wzorach błąd aproksymacji zależy liniowo od h, w ostatnim błąd jest proporcjonalny do Interpretacja geometryczna tych wzorów jest przedstawiona na rysunku 5.2.

Rys. 5.2

Uwzględnianie coraz to większej liczby węzłów w otoczeniu punktu
pozwala na konstruowanie wzorów aproksymujących
ze wzrastającym rzędem błędu ap-roksymacji. Po dołączeniu do rozwinięć (5.3) rozwinięć w szeregi Taylora dla

(5.7)

można np. uzyskać wzory następujące:

(5.8)

(5.9)

(5.10)

(5.11)

(5.12)

Wzory (5.8) ÷ (5.12) najłatwiej można otrzymać stosując metodę mnożników nieoznaczonych. Metodę tę przedstawimy na dwóch przykładach wyznaczania wzorów (5.8) i (5.10).

W celu wyprowadzenia wzoru (5.8) rozważymy dwa rozwinięcia:

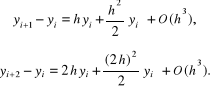
Drugie z tych równań mnożymy przez na razie nieokreślony czynnik a i dodajemy je stronami. Po uporządkowaniu otrzymamy

(5.13)

Z warunku, aby znikał współczynnik przy
obliczamy mnożnik a

i następnie uzyskujemy wzór (5.8).

Przy wyprowadzaniu wzoru (5.10) wykorzystujemy trzy następujące rozwinięcia:

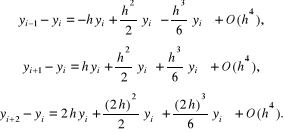
Po pomnożeniu drugiego z tych równań przez a, trzeciego przez b i dodaniu wszystkich równań stronami dostajemy zależność

(5.14)

z której z warunków znikania współczynników przy pochodnych
i
otrzymujemy układ równań:

Stąd wynikają wartości a i b:

i ostatecznie wzór (5.10).

Wzór aproksymujący drugą pochodną
za pomocą wartości funkcji w punkcie
oraz w punktach
i
wynika bezpośrednio z rozwinięć (5.3)

(5.15)

Inny wzór aproksymujący
możemy otrzymać z zależności (5.13) dla

(5.16)

Ważne w zastosowaniach praktycznych wzory dla pochodnych uzyskane przy uwzględnieniu wartości funkcji
w pięciu kolejnych węzłach:
,
,
,
,
, przedstawimy w postaci

(5.17)

Podstawiając do zależności (5.17) rozwinięcia dla
i
w szeregi Taylora z błędem
po porównaniu wyrazów występujących przy

po lewej i prawej jej stronie, otrzymamy układ równań, z którego obliczymy nieznane współczynniki a, b, c, d i e. Przykładowo dla r = 2 układ ten ma postać:

Stąd wyznaczamy:

i ostatecznie mamy

(5.18)

W podobny sposób uzyskujemy:

(5.19)

(5.20)

*

Jakość aproksymacji rozważanych operatorów różnicowych wygodnie jest ilościowo ująć opierając się na analizie odnoszącej się do pojedynczego modu Fouriera [23]. Analiza taka pozwala bowiem oszacować dokładność aproksymacji różnicowej w zjawiskach o różnych długościach fal.

Dla przykładu przeanalizujemy aproksymacje pierwszej i drugiej pochodnej ilorazami różnicowymi (5.6) i (5.15) dla modu fourierowskiego

(5.21)

w którym g jest amplitudą, k - liczbą falową a i - pierwiastkiem z liczby

Po wstawieniu modu (5.21) do ilorazu różnicowego (5.6)

i rozwinięciu następnie w szereg dostajemy

(5.22)

Porównując otrzymany wzór ze wzorem na pochodną modu (5.21)

260 5. Różniczkowanie, całkowanie i aproksymacja

5.1. Różniczkowanie numeryczne i aproksymacja pochodnych 261

---