Laboratoryjne zajęcie N6

Weryfikacja modeli ekonometrycznych

Badanie symetrii składnika losowego

Rozkład normalny o parametrach (m, σ²) jest symetryczny, przy tym jego oś symetrii przechodzi przez punkt x = m, tzn. jeżeli zmienna losowa ξ ma rozkład N(m, σ²), to

P{ ξ < m } = P{ ξ ≥ m } =
.

Sprawdzenie symetrii rozkładu składnika losowego sprowadza się do weryfikacji hipotezy:

H: P(e_i < 0) = P(e_i ≥ 0) =
.

Innymi słowy należy zbadać równość prawdopodobieństwa występowania dodatnich i ujemnych reszt. Oznaczmy przez m₊ liczbę nieujemnych spośród n podlegających badaniu reszt e_t , t = 1, 2, …, n. Jeśli weryfikowana hipoteza jest prawidłowa, to m₊ ma rozkład dwumianowy o parametrach (n, 0,5):

m₊: B(n, 0,5).

Obszar krytyczny testu weryfikacji hipotezy symetrii dla dowolnych, z góry założonych poziomów istotności γ ma postać następującego zbioru liczb całkowitych:

Q = {0, 1, ..., m₁}  {m₂, m₂ + 1, ..., n},

gdzie wartości krytyczne m₁ oraz m₂ określono na podstawie równości:

P{m₁ < B(n, 0,5) < m₂} ≥ 1 - γ .

Weryfikacja hipotezy odbywa się następująco:

• Za pomocą tablicy testu symetrii określamy krytyczne wartości m₁, m₂. Jeżeli się okaże, że spełniony jest warunek:

m₁ < m₊ < m₂,

to uznajemy wówczas, że nie ma podstaw do odrzucenia hipotezy symetrii składnika losowego.

• Natomiast jeżeli m₊ ∈ Q, (tzn. m₊ ≤ m₁, lub m₊ ≥ m₂), to wtedy hipoteza o symetrii składnika losowego podlega odrzuceniu.

Badanie losowości składnika losowego

Dla sprawdzenia stochastycznego charakteru, czyli krótko losowości, składnika losowego służy test serii. Podstawowym pojęciem testu jest pojęcie serii:

• Jeżeli symbol (+) oznacza resztę dodatnią, natomiast symbol (-) - resztę ujemną, to każdy podciąg ciągu reszt e₁, e₂, e_n. który zawiera tylko elementy jednego rodzaju (+) lub (-) bezpośrednio po sobie następujące, nosi nazwę serii.

Innymi słowy, serią jest każdy podciąg uszeregowanego ciągu reszt złożonych wyłącznie z elementów dodatnich lub ujemnych.

Załóżmy, że wśród reszt e₁, e₂, e_n występuje dokładnie n₁ wartości dodatnich i n₂ wartości ujemnych (n₁ + n₂ = n). Obszar krytyczny testu weryfikacji hipotezy losowości ma postać następującego zbioru liczb całkowitych:

Q = {0, 1, ..., S₁}  {S₂, S₂ + 1, ..., n},

gdzie wartości krytyczne S₁ oraz S₂ określono na podstawie rozkładu prawdopodobieństwa zmiennej losowej ς(n₁, n₂), która oznacza liczbę serii dla określonego wyżej ciągu reszt e₁, e₂, e_n.

Weryfikacja hipotezy odbywa się następująco:

• Dla uszeregowanego ciągu reszt e₁, e₂, e_n określiamy liczbę serii S, liczbę n₁ reszt dodatnich oraz liczbę n₂ reszt ujemnych.

• Za pomocą tablicy testu serii określamy dwie krytyczne liczby serii S₁*, S₂*.

• Jeśli się okaże, iż

S₁* < S < S₂*.

to nie ma podstaw do odrzucenia badanej hipotezy losowości składnika losowego. Oznacza to, że rozkład odchyleń losowych jest losowy, a postać analityczna modelu została dobrana trafnie.

• Jeżeli m₊ ∈ Q, (tzn. S ≤ S₁*, lub S ≥ S₂*), to wtedy hipoteza o losowości składnika losowego podlega odrzuceniu.

Badanie normalności składnika losowego.

Test zgodności Hellwiga, aby zweryfikować hipotezę, że składnik losowy podlega prawu rozkładu normalnego, w roli wskaźnika dopasowania rozkładów teoretycznych i empirycznych wybiera statystykę, określająca liczbę „cel pustych”.

Weryfikacja hipotezy odbywa się następująco:

• Dokonuje się standaryzacji reszt według wzoru:
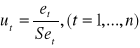
  , gdzie Se_t - odchylenie standardowe reszt e_t, (t = 1, 2, ..., n), obliczane według wzoru:

.

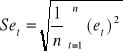
• Standaryzowane reszty uporządkowuje się według wartości niemalejących tak, że

u*₁ < u*₂ < ... u*_n.

• Za pomocą funkcji „ROZKŁAD NORMALNY.S.” oblicza się wartości F_N(u*_t).

• Odcinek [0,1] dzielimy na n równych części tzw. cele I_t, (t = 1, 2, ..., n), którymi są przedziały liczbowe o rozpiętości 1/n powstałe po podzieleniu odcinka [0,1].

• Wartości dystrybuanty F_N(u*_t) przyporządkowuje się odpowiednim celom i określa się liczbę cel pustych K.

• Z tablic testu zgodności Hellwiga dla danej liczby obserwacji n oraz dla przyjętego poziomu istotności γ odczytuje się dwie krytyczne liczby cel pustych K₁*, K₂*.

• Jeśli się okaże, iż

K₁* < K < K₂*.

to nie ma podstaw do odrzucenia badanej hipotezy.

• Jeżeli K ≤ K₁*, lub K ≥ K₂*, to wtedy hipoteza o normalności rozkładu składnika losowego podlega odrzuceniu.

Tablica wartości krytycznych testu symetrii rozkładu składnika losowego

n	m1	m2	n	m1	m2	n	m1	m2	n	m1	m2	n	m1	m2
6	1	5	11	3	8	16	4	12	21	6	15	26	8	18
7	1	6	12	3	9	17	4	13	22	7	15	27	9	18
8	2	6	13	3	10	18	5	13	23	7	16	28	9	19
9	2	7	14	4	10	19	5	14	24	7	17	29	9	20
10	2	8	15	4	11	20	6	14	25	8	17	30	10	20

Tablica wartości krytycznych testu liczby serii

(wartości S₁)

n2n1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
2
3
4			2
5		2	2	3
6		2	3	3	3
7		2	3	3	4	4
8	2	2	3	3	4	4	5
9	2	2	3	4	4	5	5	6
10	2	3	3	4	5	5	6	6	6
11	2	3	3	4	5	5	6	6	7	7
12	2	3	4	4	5	6	6	7	7	8	8
13	2	3	4	4	5	6	6	7	8	8	9	9
14	2	3	4	5	5	6	7	7	8	8	9	9	10
15	2	3	4	5	6	6	7	8	8	9	9	10	10	11

(wartości S₂)

n2n1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
2	4
3	5	6
4	5	6	7
5	5	7	8	8
6	5	7	8	9	10
7	5	7	8	9	10	11
8	5	7	9	10	11	12	12
9	5	7	9	10	11	12	13	13
10	5	7	9	10	11	12	13	14	15
11	5	7	9	11	12	13	14	14	15	16
12	5	7	9	11	12	13	14	15	16	16	17
13	5	7	9	11	12	13	14	15	16	17	17	18
14	5	7	9	11	12	13	15	16	16	17	18	19	19
15	5	7	9	11	13	14	15	16	17	18	18	19	20	20

Tablica wartości krytycznych testu zgodności Hellwiga dla poziomu istotności γ = 0,05

n	6	8	10	12	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30
K1*	0	0	1	2	2	2	3	3	3	4	4	4	5	5	5	5	6	6	6	6	7
K2*	3	4	5	6	7	7	8	8	9	9	9	10	10	11	11	12	12	12	13	13	14

---