PROGRAM 3.2.

Rozwiązywanie równania nieliniowego:

f(x) = x - sin(x) - 0.25 = 0.

Klasyczna i zmodyfikowana metoda Newtona.

Przybliżenie początkowe - x0 = 9.0000000E-0001

Dokładność obliczeń - eps = 1.0E-0009

Klasyczna metoda Newtona.

Pierwiastek równania - ksi = 1.1712297E+0000

Residuum równania: f(ksi) = 1.05E-0010

Liczba iteracji: 5

Zmodyfikowana metoda Newtona.

Pierwiastek rownania - ksi = 1.1712297E+0000

Residuum rownania: f(ksi) = -3.02E-0010

Liczba iteracji: 41

3.3. Dwupunktowe metody iteracyjne

Najprostszą iteracyjną metodą dwupunktową wyznaczania pierwiastków równania (3.1) jest metoda bisekcji (połowienia). Przy założeniu, że wewnątrz przedziału [a, b] znajduje się dokładnie jeden pierwiastek równania (3.1) oraz że na końcach tego przedziału wartości funkcji
mają przeciwne znaki metoda bisekcji dla generuje ciąg punktów zdefiniowany następującym algorytmem:

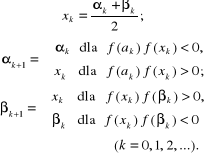
(3.25)

Interpretacja geometryczna procesu iteracyjnego (3.25) jest bardzo prosta: w każdym kroku dzielimy przedział na połowę i z otrzymanych dwóch podprzedziałów wybieramy ten, w którym na pewno znajduje się pierwiastek równania (3.1). W wyniku takiego postępowania po pewnej liczbie kroków albo otrzymujemy pierwiastek dokładny albo otrzymujemy pierwiastek przybliżony obarczony błędem będącym długością podprzedziału

(3.26)

Zatem metoda bisekcji jest zbieżna liniowo, ze stałą asymptotyczną błędu

{Program 3.3}

unit Obliczenia;

interface

uses

Windows, Messages, SysUtils, Classes, Graphics, Controls,

Forms, Dialogs, StdCtrls, Buttons;

. . . . . . . . . . . . . . . . .

var

Form3: TForm3;

a,b,bl,eps,fa,fb,fx,x: Double;

iter: Integer;

plik: Text;

implementation

uses Ustawienia, Informacje, Grafika, Podglad;

{$R *.DFM}

function f(x: Real): Real;

begin

f:=x-Sin(x)-0.25;

end;

. . . . . . . . . . . . . . . . . . . . . .

procedure TForm3.BitBtn1Click(Sender: TObject);

label omin;

begin

Form2.Show;

AssignFile(plik,Edit4.Text);

Rewrite(plik); Writeln(plik,'PROGRAM 3.3.');

Writeln(plik,'Rozwiązywanie równania nieliniowego:');

Writeln(plik,' f(x) = x - sin(x) - 0.25 = 0.');

Writeln(plik,'Metoda bisekcji.'); Writeln(plik,'');

Writeln(plik,'Przedział izolacji pierwiastka:');

a:=StrToFloat(Edit1.Text);

b:=StrToFloat(Edit2.Text);

Writeln(plik,'Lewy koniec przedziału - a = ',a:6);

Writeln(plik,'Prawy koniec przedziału - b = ',b:6);

fa:=f(a); Writeln(plik,' f(a) = ',fa:18);

fb:=f(b); Writeln(plik,' f(b) = ',fb:18);

if fa*fb>0 then begin

Writeln(plik,'Wartosci funkcji na końcach przedziału [a,b]');

Writeln(plik,'nie są różnych znaków.');

Writeln(plik,'');

goto omin;

end;

eps:=StrToFloat(Edit3.Text);

Writeln(plik,'Dokładność obliczeń - eps = ',eps:9);

Writeln(plik,''); iter:=0;

repeat

x:=(a+b)/2;

fx:=f(x);

if fx*fa<0 then begin

b:=x; fb:=fx;

end else begin

a:=x; fa:=fx;

end;

iter:=iter+1;

bl:=Abs(b-a);

until (bl<eps) or (Abs(fx)<eps);

Writeln(plik,'Pierwiastek równania - ksi = ',x:18);

Writeln(plik,'Residuum równania: f(ksi) = ',fx:11);

Writeln(plik,'Liczba iteracji: ',iter);

omin:

CloseFile(plik);

Form2.Wyniki.Lines.LoadFromFile(Edit4.Text);

end;

. . . . . . . . . . . . . . . . . . . . . . .

procedure TForm3.BitBtn3Click(Sender: TObject);

begin

Close;

end;

end.

Zadaniem programu 3.3 jest rozwiązywanie równania (3.18) metodą bisekcji dla zadanego przedziału izolacji pierwiastka [a, b] i zadanej dokładności obliczeń ε . Otrzymane wyniki obliczeń dla a = 0.1, b = 1.5 i
są następujące:

PROGRAM 3.3.

Rozwiązywanie równania nieliniowego:

f(x) = x - sin(x) - 0.25 = 0.

Metoda bisekcji.

Przedział izolacji pierwiastka:

początek przedziału - a = 1.0E-0001

koniec przedziału - b = 1.5E+0000

f(a) = -2.498334166E-0001

f(b) = 2.525050134E-0001

Dokładność obliczeń - eps = 1.0E-0009

Pierwiastek równania - ksi = 1.171229653E+0000

Residuum równania: f(ksi) = 5.69E-0010

Liczba iteracji: 29

*

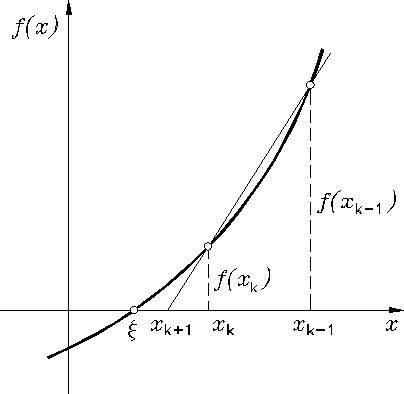
Rys. 3.3

Następną, bardzo popularną dwupunktową metodą iteracyjną jest metoda siecznych, w której dla obliczenia przybliżenia pierwiastka ξ funkcja
jest aproksymowana prostą przechodzącą przez dwa punkty o odciętych: i rzędnych: (rys. 3.3).

Z podobieństwa dwóch trójkątów uwidocznionych na rysunku 3.3 wynika, że

skąd wyznaczamy

. (3.27)

Otrzymaną zależność rekurencyjną można również przedstawić w postaci

, (3.28)

przypominającej zależność rekurencyjną (3.19) dla metody stycznych - z tą różnicą, że pochodna została zastąpiona ilorazem różnicowym.

Metoda siecznych może być stosowana zarówno, gdy

jak i w przypadku przeciwnym, gdy

Przy stosowaniu tej metody powinno się jednak jako przybliżenia początkowe wybierać takie dwa punkty, w których funkcja
ma różne znaki; w przeciwnym wypadku można bowiem wykryć nieistniejący pierwiastek (rys. 3.4).

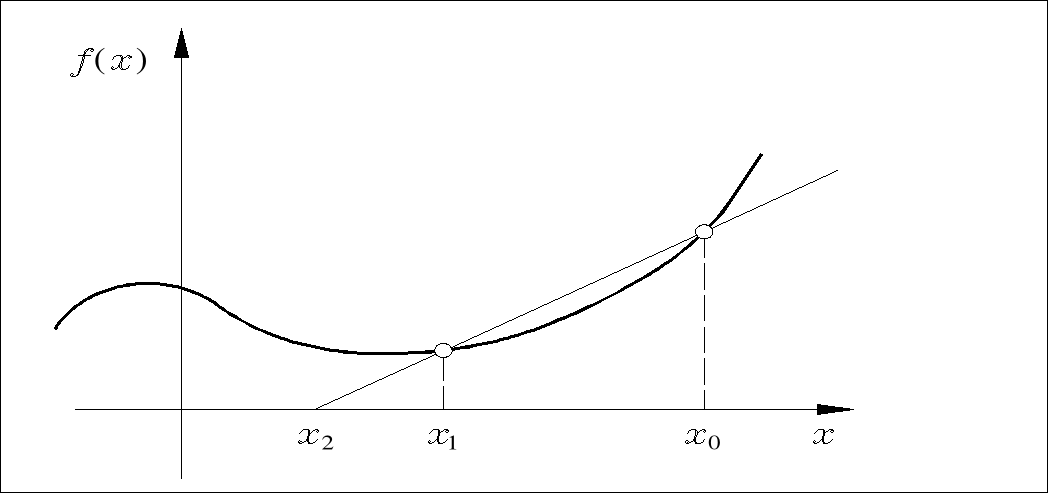
Rys. 3.4

W przypadku, gdy w rozpatrywanym przedziale [a, b] równanie (3.1) ma dok-ładnie jeden pierwiastek oraz gdy pochodne
i
funkcji
mają sta-ły znak w tym przedziale, jeden z punktów w kolejnych przybliżeniach można przy-jąć jako nieruchomy. Otrzymamy w ten sposób szczególną jednopunktową wersję metody siecznych, zwaną metodą regula falsi (z łacińskiego: regula - linia, falsus -fałszywy, co oznacza metodę fałszywego założenia liniowości funkcji). Punktem stałym w metodzie regula falsi jest ten punkt, w którym znak drugiej pochodnej
jest taki sam jak znak funkcji Zatem dla funkcji
przedstawionej na rysunku 3.5a punktem stałym będzie punkt

(3.29)

Rys. 3.5

a dla funkcji przedstawionej na rysunku 3.5b punkt

(3.30)

Błąd przybliżenia pierwiastka ξ obliczonego metodą regula falsi można oszacować w następujący sposób [2, 9]:

(3.31)

gdzie wielkości i
oznaczają, odpowiednio, najmniejszą i największą wartość modułu pochodnej
na odcinku [a, b]. Jeśli odcinek [a, b] jest dostatecznie mały wtedy zachodzi nierówność

i ze wzoru (3.31) otrzymujemy oszacowanie

Przerwanie obliczeń w chwili, gdy gwarantuje więc również obliczenie pierwiastków z taką samą dokładnością.

{Program 3.4}

unit Obliczenia;

interface

uses

Windows, Messages, SysUtils, Classes, Graphics, Controls,

Forms, Dialogs, StdCtrls, Buttons;

. . . . . . . . . . . . . . . . .

var

Form3: TForm3;

bl,blp,eps,fx,fx0,fx1,x,x0,x1: Double;

iter: Integer;

plik: Text;

implementation

uses Ustawienia, Informacje, Grafika, Podglad;

{$R *.DFM}

function f(x: Real): Real;

begin

f:=x-Sin(x)-0.25;

end;

. . . . . . . . . . . . . . . . . . . . . .

procedure TForm3.BitBtn1Click(Sender: TObject);

label omin;

begin

Form2.Show;

AssignFile(plik,Edit4.Text);

Rewrite(plik); Writeln(plik,'PROGRAM 3.4.');

Writeln(plik,'Rozwiązywanie równania nieliniowego:');

Writeln(plik,' f(x) = x - sin(x) - 0.25 = 0.');

Writeln(plik,'Metoda siecznych.');

Writeln(plik,'');

x0:=StrToFloat(Edit1.Text);

x1:=StrToFloat(Edit2.Text);

Writeln(plik,'Przybliżenia początkowe:');

Writeln(plik,' x0 = ',x0:6);

Writeln(plik,' x1 = ',x1:6);

fx0:=f(x0);

Writeln(plik,' f(x0) = ',fx0:18);

fx1:=f(x1);

Writeln(plik,' f(x1) = ',fx1:18);

eps:=StrToFloat(Edit3.Text);

Writeln(plik,'Dokładność obliczeń - eps = ',eps:9);

Writeln(plik,''); blp:=1e10; iter:=0;

repeat

x:=(fx1*x0-fx0*x1)/(fx1-fx0);

fx:=f(x); bl:=Abs(x-x1);

if bl>blp then begin

Writeln(plik,'Proces iteracyjny jest rozbieżny');

Writeln(plik,''); goto omin;

end else blp:=bl;

x0:=x1; fx0:=fx1;

142 3. Równania nieliniowe

3.3. Dwupunktowe metody iteracyjne 143

---