Rozdział 6
RÓWNANIA RÓŻNICZKOWE ZWYCZAJNE
I CAŁKOWE
6.1. Zagadnienia początkowe dla równań różniczkowych
zwyczajnych
6.1.1. Wiadomości ogólne
Różne procesy fizyczne są opisywane równaniami różniczkowymi zwyczajny-mi, zawierającymi funkcje niewiadome, zmienne niezależne oraz pochodne funkcji niewiadomych. Metody rozwiązywania zagadnień opisywanych takimi równaniami mają więc ważne znaczenie w nauce i technice. Chociaż wiele rodzajów równań różniczkowych zwyczajnych może być rozwiązanych metodami analitycznymi, to jednak znaczna - mająca ważne znaczenie fizyczne - część tych równań może być rozwiązana tylko w sposób przybliżony.
W najprostszym przypadku równania różniczkowego zwyczajnego pierwszego rzędu szukamy pewnej funkcji różniczkowalnej ![]()
zmiennej rzeczywistej x, której pochodna spełnia równanie postaci
(6.1)
Uogólnieniem równania (6.1) jest układ n równań różniczkowych zwyczajnych:
(6.2)
dla n szukanych funkcji rzeczywistych ( i = 1, 2, ..., n), jednej zmiennej rzeczywistej x.
Wprowadzając wektory kolumnowe:
(6.3)
możemy układ równań (6.2) zapisać w postaci wektorowej
(6.4)
Oprócz równań różniczkowych zwyczajnych rzędu pierwszego występują także równania różniczkowe zwyczajne rzędu m o postaci
(6.5)
Równania te można przekształcić w równoważny układ równań pierwszego rzędu:
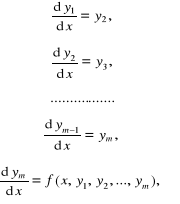
(6.6)
po wprowadzeniu funkcji pomocniczych:
(6.7)
Równanie (6.5) jest równaniem różniczkowym zwyczajnym rozwiązanym względem najwyższej pochodnej. W ogólnym przypadku wyrażenie m-tej pochodnej w sposób jawny może okazać się niemożliwe, wtedy równanie różniczkowe zwyczajne m-tego rzędu przyjmuje postać
![]()
(6.8)
Na ogół istnieje nieskończenie wiele funkcji będących rozwiązaniami pojedynczych równań różniczkowych lub układów równań różniczkowych zwyczajnych. Ze zbioru wszystkich rozwiązań wyróżniamy zazwyczaj pewne szczególne rozwiązania za pomocą dodatkowych warunków nakładanych na funkcje niewiadome. Te dodatkowe warunki mogą być określone w jednym punkcie lub w wielu punktach przedziału [a, b]. W pierwszym przypadku noszą one nazwę warunków początkowych, w drugim - warunków brzegowych.
*
Przez zagadnienie początkowe dla pojedynczego równania różniczkowego pierwszego rzędu (6.1):
(6.9)
rozumiemy zadanie znalezienia różniczkowalnej funkcji która spełnia równa-nie różniczkowe (6.1) oraz przybiera zadaną wartość ya w punkcie Podobnie formułujemy zagadnienie początkowe dla układu równań różniczkowych zwyczajnych (6.4):
(6.10)
Zagadnienia początkowe (6.9), (6.10) mają dokładnie jedno rozwiązanie, gdy funkcje ![]()
( i = 1, 2, ..., n) są ograniczone i ciągłe oraz spełniają warunek Lipschitza względem argumentów: ![]()
[26].
Metody i algorytmy rozwiązywania zagadnień początkowych w przypadku układów równań różniczkowych zwyczajnych pierwszego rzędu są na ogół niezależne od
liczby n funkcji niewiadomych. Dlatego też ograniczymy się do rozważania zagadnienia początkowego (6.9) dla jednej tylko funkcji niewiadomej.
Metody przybliżone rozwiązywania zagadnień początkowych można podzielić na trzy podstawowe grupy:
1. Analityczne, polegające na poszukiwaniu rozwiązania zagadnienia różniczkowego w postaci odpowiedniego wyrażenia analitycznego.
2. Analityczno-numeryczne, wymagające zastosowania operacji numerycznych w celu wyznaczenia współczynników występujących w założonej postaci rozwiązania.
3. Numeryczne (dyskretne) - odznaczające się tym, że rozwiązanie zagadnienia (6.9) wyznacza się w dyskretnych punktach przedziału [a, b].
Najważniejszymi metodami dyskretnymi są:
- metody Rungego-Kutty,
- metody wielokrokowe liniowe.
W metodach numerycznych operatory różniczkowe zastępujemy różnego rodzaju operatorami różnicowymi, które muszą spełniać warunki zgodności, zbieżności i stabilności, aby możliwie najdokładniej odtworzyć kształt rozwiązania zagadnienia rózniczkowego w zadanym przedziale [a, b].
Zgodność aproksymacji różnicowej z układem różniczkowym jest wymaganiem, aby w granicy małych kroków układ różnicowy był identyczny z układem różniczkowym.
Metodę numeryczną nazywamy zbieżną, jeśli w wyniku przejścia od argumentów i funkcji dyskretnych do argumentów i funkcji ciągłych dają się zlikwidować błędy między rozwiązaniem ścisłym, a rozwiązaniem przybliżonym. Oznacza to, że nie występuje zjawisko kumulacji błędów całkowitych, które wraz z zagęszczeniem podziału dążą do zera dla wszystkich punktów podziału.
Metoda numeryczna jest stabilna, jeśli mały błąd powstający na dowolnym etapie obliczeń przenosi się dalej z malejącą amplitudą. O schemacie różnicowym powodującym narastanie błędu mówimy, że jest niestabilny numerycznie. Pojęcie stabilności odnosi się zarówno do błędu aproksymacji (błędu metody) - jaki wnosi sama metoda w jednym kroku obliczeń bez uwzględnienia wpływu błędów popełnionych we wcześniejszych krokach, jak i do błędów zaokrąglenia, mogących pojawić się na każdym etapie obliczeń. W pewnych zagadnieniach fizycznych mogą wystąpić rozwiązania rosnące wykładniczo - z czego wynika, że warunkowo dopuszczalny jest również wzrost błędu, byle tylko pozostawał on mniejszy od rosnącego rozwiązania.
6.1.2. Metody analityczne i analityczno-numeryczne
Do najważniejszych metod analitycznych należą: metoda rozwijania rozwiązania w szereg Taylora oraz metoda kolejnych przybliżeń Picarda. Przykładem metody analityczno-numerycznej jest również metoda oparta na wykorzystaniu funkcji sklejanych trzeciego stopnia.
Jeśli w zagadnieniu początkowym (6.9) funkcja ![]()
ma pochodne dowolnie wysokiego rzędu względem obu swych argumentów oraz jeśli jest rozwijalna w szereg potęgowy w otoczeniu punktu początkowego
![]()
to rozwiązanie zagadnienia początkowego (6.9) ma postać szeregu potęgowego [27]
(6.11)
Wartości pochodnych funkcji w punkcie wyznaczamy z danego równania różniczkowego przez kolejne różniczkowanie i podstawianie danych warunków początkowych. Metodę tę można stosować do równań dowolnego rzędu.
Napiszemy kilka wyrazów rozwinięcia rozwiązania równania
(6.12)
spełniającego warunki początkowe:
w szereg potęgowy (6.11).
Z równania (6.12) otrzymujemy
(6.13)
stąd
Różniczkując kolejno równanie (6.13) mamy:
...............................
i następnie obliczamy:
;
zatem
.
Wiadomo [27], że jeśli istnieje rozwiązanie zagadnienia początkowego (6.9), to jest ono granicą ciągu kolejnych przybliżeń Picarda zdefiniowanych wzorem rekurencyjnym
![]()
(6.14)
Ciąg ten jest zbieżny w pewnym otoczeniu punktu x = a niezależnie od wyboru przybliżenia początkowego. Najprościej jest przyjąć za przybliżenie wyjściowe funkcję stałą
Znajdziemy przybliżone rozwiązanie zagadnienia:
(6.15)
Biorąc za przybliżenie wyjściowe funkcję
= ![]()
= 0
dostajemy:
![]()
![]()
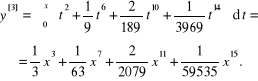
Przy różnica między i nie przekracza wielkości
*
Metoda funkcji sklejanych opiera się na aproksymacji rozwiązania zagadnienia (6.9) funkcją sklejaną trzeciego stopnia, którą w każdym podprzedziale
przedziału [a, b] zapiszemy w postaci
(6.16)
gdzie:
Po zróżniczkowaniu (6.16) otrzymujemy:
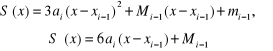
(6.17)
i następnie mamy:
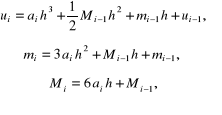
(6.18)
gdzie
Z warunku spełnienia równania (6.9a) przez funkcję w punkcie
![]()
(6.19)
uzyskujemy, po wykorzystaniu (6.18a) i (6.18b), równanie dla nieznanego współ-czynnika Początkowe wartości i wynikają z warunku początkowego i równania (6.9a):
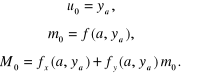
(6.20)
Jeśli ![]()
to istnieje taka stała L, że dla wszystkich h < 3/L (L - stała Lipschitza) i dla wszystkich ![]()
słuszne jest oszacowanie [28]
(6.21)
Przedstawiony algorytm rozwiązywania zagadnienia początkowego (6.9) metodą funkcji sklejanych wymaga rozwiązania w każdym podprzedziale (i = 1, 2, ..., N) równania (6.19) względem nieznanego współczynnika Współczynnik ten można wyznaczyć iteracyjnie po przyjęciu jego wstępnej wartości równej zeru.
{Program 6.1}
uses
Crt;
var
i,n: Integer;
a,akp,akn,b,der1n,der1p,der2a,der2n,
der2p,eps,h,h2,up,un,x,y,ya: Real;
plik: Text;
label powt;
function f(x,y: Real): Real;
begin
f:=y-2*x/y;
end;
function yd(x: Real): Real;
begin
yd:=Sqrt(2*x+1);
end;
begin
Assign(plik,'Pr_6_1.wyn');
Rewrite(plik);
Writeln(plik,'PROGRAM 6.1');
Writeln(plik,'Zagadnienie poczatkowe dla rownania');
Writeln(plik,'rozniczkowego zwyczajnego.');
Writeln(plik,'Metoda funkcji sklejanych.');
Writeln(plik); ClrScr;
Writeln('PROGRAM 6.1. Dane do obliczen:');
Write(' - poczatek przedzialu: a = '); Readln(a);
Write(' - koniec przedzialu: b = '); Readln(b);
Write(' - liczba podprzedzialow: n = '); Readln(n);
Write(' - warunek poczatkowy: ya = '); Readln(ya);
Write(' - warunek dodatkowy: der2a = '); Readln(der2a);
Write(' - dokladnosc obliczen: eps = '); Readln(eps);
Writeln(plik,'Poczatek przedzialu: a = ',a:13);
Writeln(plik,'Koniec przedzialu: b = ',b:13);
Writeln(plik,'Liczba podprzedzialow: n = ',n:3);
Writeln(plik,'Warunek poczatkowy: ya = ',ya:13);
Writeln(plik,'Warunek dodatkowy: der2a = ',der2a:13);
Writeln(plik,'Dokladnosc obliczen: eps = ',eps:13);
Writeln(plik);
Writeln(plik,'Obliczone wartosci funkcji:');
Writeln(plik,' i x[i] y[i] blad');
Writeln(plik,0:3,' ',a:13,' ',ya:13,' ',ya-ya:13);
h:=(b-a)/n;
up:=ya;
der1p:=f(a,ya);
der2p:=der2a;
akp:=0; h2:=h*h;
for i:=1 to n do begin
x:=a+i*h;
powt:
un:=up+der1p*h+0.5*der2p*h2+akp*h*h2;
akn:=(f(x,un)-der1p-der2p*h)/h2/3;
if Abs(akn-akp)>eps then begin
akp:=akn; goto powt;
end;
up:=un; y:=yd(x);
der1n:=der1p+der2p*h+3*akn*h2;
der2n:=der2p+6*akn*h;
der1p:=der1n; der2p:=der2n;
Writeln(plik,i:3,' ',x:13,' ',un:13,' ',y-un:13);
end;
Writeln(plik);
Close(plik);
end.
Program 6.1 jest przeznaczony do całkowania równania
![]()
(6.22)
z warunkiem początkowym
(6.23)
metodą funkcji sklejanych. Uzyskane wyniki obliczeń dla: h = 0.1, ![]()
i porównanie z rozwiązaniem dokładnym
![]()
(6.24)
zawiera poniższy tabulogram:
PROGRAM 6.1
Zagadnienie poczatkowe dla rownania
rozniczkowego zwyczajnego.
Metoda funkcji sklejanych.
Poczatek przedzialu: a = 0.000000E+00
Koniec przedzialu: b = 2.000000E+00
Liczba podprzedzialow: n = 20
Warunek poczatkowy: ya = 1.000000E+00
Warunek dodatkowy: der2a = -1.000000E+00
Dokladnosc obliczen: eps = 1.000000E-08
Obliczone wartosci funkcji:
k x[k] y[k] blad
0 0.000000E+00 1.000000E+00 0.000000E+00
1 1.000000E-01 1.095428E+00 1.673484E-05
2 2.000000E-01 1.183219E+00 -2.827052E-06
3 3.000000E-01 1.264896E+00 1.495681E-05
4 4.000000E-01 1.341643E+00 -1.722770E-06
5 5.000000E-01 1.414198E+00 1.523155E-05
6 6.000000E-01 1.483239E+00 7.579074E-07
7 7.000000E-01 1.549177E+00 1.669116E-05
8 8.000000E-01 1.612447E+00 4.324665E-06
9 9.000000E-01 1.673301E+00 1.940687E-05
346 6. Równania różniczkowe zwyczajne i całkowe
345
6.1. Zagadnienia początkowe dla równań różniczkowych zwyczajnych
Wyszukiwarka
Podobne podstrony:
7 h, Informatyka, Informatyka, Informatyka. Metody numeryczne, Kosma Z - Metody i algorytmy numerycz
Spis tresci, Informatyka, Informatyka, Informatyka. Metody numeryczne, Kosma Z - Metody i algorytmy
4 a, Informatyka, Informatyka, Informatyka. Metody numeryczne, Kosma Z - Metody i algorytmy numerycz
1 c, Informatyka, Informatyka, Informatyka. Metody numeryczne, Kosma Z - Metody i algorytmy numerycz
4 m, Informatyka, Informatyka, Informatyka. Metody numeryczne, Kosma Z - Metody i algorytmy numerycz
Okladka, Informatyka, Informatyka, Informatyka. Metody numeryczne, Kosma Z - Metody i algorytmy nume
1 h, Informatyka, Informatyka, Informatyka. Metody numeryczne, Kosma Z - Metody i algorytmy numerycz
Przedmowa, Informatyka, Informatyka, Informatyka. Metody numeryczne, Kosma Z - Metody i algorytmy nu
Contents, Informatyka, Informatyka, Informatyka. Metody numeryczne, Kosma Z - Metody i algorytmy num
4 i, Informatyka, Informatyka, Informatyka. Metody numeryczne, Kosma Z - Metody i algorytmy numerycz
6 c, Informatyka, Informatyka, Informatyka. Metody numeryczne, Kosma Z - Metody i algorytmy numerycz
5 f, Informatyka, Informatyka, Informatyka. Metody numeryczne, Kosma Z - Metody i algorytmy numerycz
2 c, Informatyka, Informatyka, Informatyka. Metody numeryczne, Kosma Z - Metody i algorytmy numerycz
2 f, Informatyka, Informatyka, Informatyka. Metody numeryczne, Kosma Z - Metody i algorytmy numerycz
1 d, Informatyka, Informatyka, Informatyka. Metody numeryczne, Kosma Z - Metody i algorytmy numerycz
7 c 2, Informatyka, Informatyka, Informatyka. Metody numeryczne, Kosma Z - Metody i algorytmy numery
5 h, Informatyka, Informatyka, Informatyka. Metody numeryczne, Kosma Z - Metody i algorytmy numerycz
7 b, Informatyka, Informatyka, Informatyka. Metody numeryczne, Kosma Z - Metody i algorytmy numerycz
1 e, Informatyka, Informatyka, Informatyka. Metody numeryczne, Kosma Z - Metody i algorytmy numerycz
więcej podobnych podstron