procedure TForm3.SpeedButton1Click(Sender: TObject);

begin

if SaveDialog1.Execute then begin

Dane.Lines.SaveToFile(SaveDialog1.FileName);

nazwa:=SaveDialog1.FileName;

end;

end;

end.

W celu umożliwienia porównania wyników otrzymywanych metodą eliminacji Gaussa z wynikami uzyskanymi metodą Banachiewicza powtórzono obliczenia dotyczące rozwiązywania układu równań (2.59) i wyznaczania macierzy odwrotnej do macierzy współczynników tego układu równań. Tabulogram wyników jest następujący:

PROGRAM 2.2.

Rozwiązywanie układu równań liniowych.

Metoda Banachiewicza.

Liczba równań układu - n = 3

Liczba prawych stron - m = 1

Macierz współczynników:

wiersz nr 1

1.0000000E+0000 -1.0000000E+0000 2.0000000E+0000

wiersz nr 2

2.0000000E+0000 1.0000000E+0000 -1.0000000E+0000

wiersz nr 3

1.0000000E+0000 3.0000000E+0000 -1.0000000E+0000

Wektory prawych stron:

wiersz nr 1

5.0000000E+0000

wiersz nr 2

1.0000000E+0000

wiersz nr 3

4.0000000E+0000

Wyznacznik - det = 1.1000000E+0001

Rozwiązania układów równań:

wiersz nr 1

1.0000000E+0000

wiersz nr 2

2.0000000E+0000

wiersz nr 3

3.0000000E+0000

Macierz odwrotna:

wiersz nr 1

1.8181818E-0001 4.5454545E-0001 -9.0909091E-0002

wiersz nr 2

9.0909091E-0002 -2.7272727E-0001 4.5454545E-0001

wiersz nr 3

4.5454545E-0001 -3.6363636E-0001 2.7272727E-0001

2.5. Układy równań z macierzami pasmowymi

Przy rozwiązywaniu różnych zagadnień występują często układy równań liniowych z macierzami pasmowymi - posiadającymi tę własność, że wszystkie ich elementy są zerami z wyjątkiem elementów położonych na przekątnej głównej i kilku przekątnych pobocznych. Układy takie można rozwiązywać bardzo skutecznymi
i ekonomicznymi metodami, będącymi szczególnymi przypadkami ogólnej metody eliminacji Gaussa lub ogólnej metody Banachiewicza.

Jeśli macierz A układu równań jest trójdiagonalna

(2.76)

to układ równań:

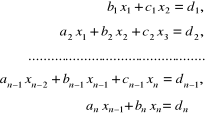
(2.77)

można rozwiązać nadzwyczaj szybko, wykonując małą liczbę działań arytmetycznych. Wykorzystując zasadę eliminacji zmiennych wyznaczamy niewiadomą
z pierwszego równania, z równania drugiego wyznaczamy niewiadomą którą podstawiamy do równania trzeciego itd. Rezultatem takiego postępowania jest algorytm, zwany metodą faktoryzacji (przeganiania, ros. pieriegonka) [10], polegający na obliczeniu najpierw wielkości pomocniczych:

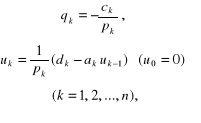
(2.78)

gdzie

a następnie niewiadomych:

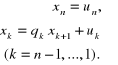
(2.79)

Metoda faktoryzacji jest niezawodna, jeśli macierz A jest diagonalnie dominująca tzn. gdy

,
.

Równie skuteczną metodą rozwiązywania układów równań z trójdiagonalnymi macierzami współczynników jest metoda, zwana algorytmem Thomasa [11], opar-ta na rozkładzie macierzy (2.76) na iloczyn Po wyznaczeniu elementów macierzy L i U ze wzorów (2.62) i (2.63):

(2.80)

gdzie:

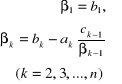
(2.81)

i obliczeniu wielkości pomocniczych (2.67):

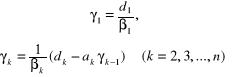
(2.82)

ze wzorów (2.68) dostajemy:

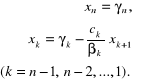
(2.83)

Układy równań z trójpasmowymi macierzami współczynników i niezerowymi elementami narożnymi

(2.84)

występują przy rozwiązywaniu zagadnień okresowych.

Rozkładając macierz A na podmacierze

, (2.85)

układ (2.84) zastępujemy dwoma układami równoważnymi:

(2.86)

gdzie:

Podstawiając

(2.87)

do pierwszego układu (2.86) uzyskujemy układy równań z trójdiagonalnymi macierzami współczynników dla wektorów i

(2.88)

Po ich rozwiązaniu niewiadomą obliczamy z drugiego równania (2.86)

(2.89)

Inny algorytm rozwiązywania układu (2.84) otrzymamy wykonując obliczenia
w następujący sposób:

1. Eliminacja zmiennych, w wyniku której zredukowany układ równań przybiera postać

(2.90)

o współczynnikach obliczanych za pomocą wzorów rekurencyjnych:

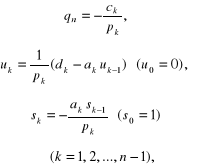
(2.91)

gdzie

2. Wyznaczanie elementów dwóch ciągów:

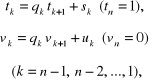
(2.92)

wynikających z podstawienia zależności

(2.93)

do wzoru (2.90).

3. Obliczanie niewiadomej z ostatniego równania układu (2.84)

(2.94)

i pozostałych niewiadomych ze wzoru (2.93).

Przedstawione algorytmy mogą być uogólnione dla układów równań o większej liczbie rozmiaru pasma zawierającego niezerowe elementy macierzy współczynników oraz dla układów równań z macierzami blokowymi.

Dla układu równań z pięciodiagonalną macierzą współczynników

(2.95)

stosując metodę faktoryzacji dla k = 1, 2, ..., n - najpierw obliczamy wielkości:

(2.96)

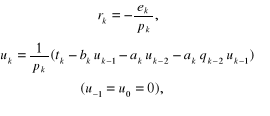
(2.96cd.)

gdzie

a potem niewiadome z zależności:

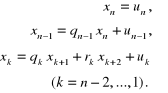
(2.97)

W przypadku układu równań z siedmiodiagonalną macierzą współczynników

(2.98)

gdzie:

w pierwszym etapie obliczeń trzeba wyznaczyć elementy czterech ciągów:

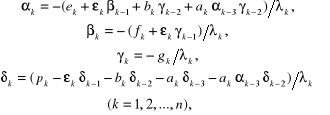
(2.99)

gdzie:

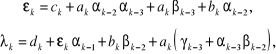
przyjmując, że początkowe ich wartości są równe zeru

W drugim etapie obliczeń wyznaczamy niewiadome ze wzorów:

(2.100)

W układach równań z macierzami blokowymi elementy macierzy współczynników są macierzami kwadratowymi, a niewiadome i elementy prawych stron są wektorami kolumnowymi.

Stosując do układu równań o trójdiagonalnej macierzy blokowej

(2.101)

ogólną zasadę eliminowania niewiadomych z układu równań o trójpasmowej macierzy współczynników wyprowadzamy wzory będące uogólnieniami związków (2.78) oraz (2.79):

Etap I

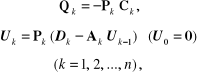
(2.102)

gdzie

Etap II

(2.103)

Podobnie rozwiązujemy układ równań z niezerowymi macierzami narożnymi

(2.104)

uogólniając wzory (2.91) ÷ (2.94):

Etap I

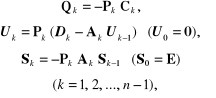
(2.105)

gdzie

Etap II

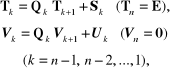
(2.106)

Etap III

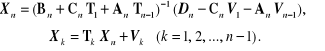
(2.107)

Dla układu równań z pięciodiagonalną macierzą blokową

(2.108)

uogólniając wzory (2.97) i (2.98), wyznaczamy najpierw macierze:

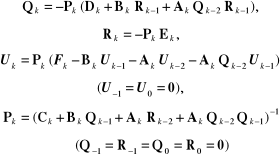
78 2. Układy równań liniowych

2.5. Układy równań z macierzami pasmowymi 79

---