4.7. Podstawowe pojęcia teorii funkcji sklejanych

Przedstawione w rozdziale poprzednim trudności, wynikające z zastosowania interpolacji wielomianowej, zmusiły do poszukiwania nowych sposobów przybliżania funkcji. Jedną z możliwości obejścia tych trudności jest wykorzystanie zamiast jednego wielomianu wysokiego stopnia przybliżającego funkcję w całym przedziale, wielu wielomianów niższego stopnia, z których każdy przybliża tę funkcję w innym podprzedziale przedziału
Dla uzyskania przybliżenia funkcji z określoną gładkością należy jeszcze odpowiednio uzgodnić (skleić)
ze sobą kolejne wielomiany; otrzymamy w ten sposób gładkie - „kawałkami wielomianowe” funkcje o jednorodnej strukturze, będące zbiorem wielomianów tego samego stopnia. Nazywane są one najczęściej w literaturze polskojęzycznej wielomianowymi funkcjami sklejanymi; obok tej nazwy stosuje się też następujące: s-funkcje, funkcje gięte, spline-funkcje czy też spline'y.

Nazwa „spline” przeniesiona została z języka angielskiego: oznacza ona listewkę (giętkę) wykorzystywaną przez kreślarzy do wykreślania gładkich krzywych przechodzących przez zadane punkty. Można to osiągnąć po umocowaniu giętki w zadanym punkcie np.
i odpowiednim przemieszczaniu podpór, których liczba jest ustalana w trakcie „dopasowywania” giętki - rys. 4.12.

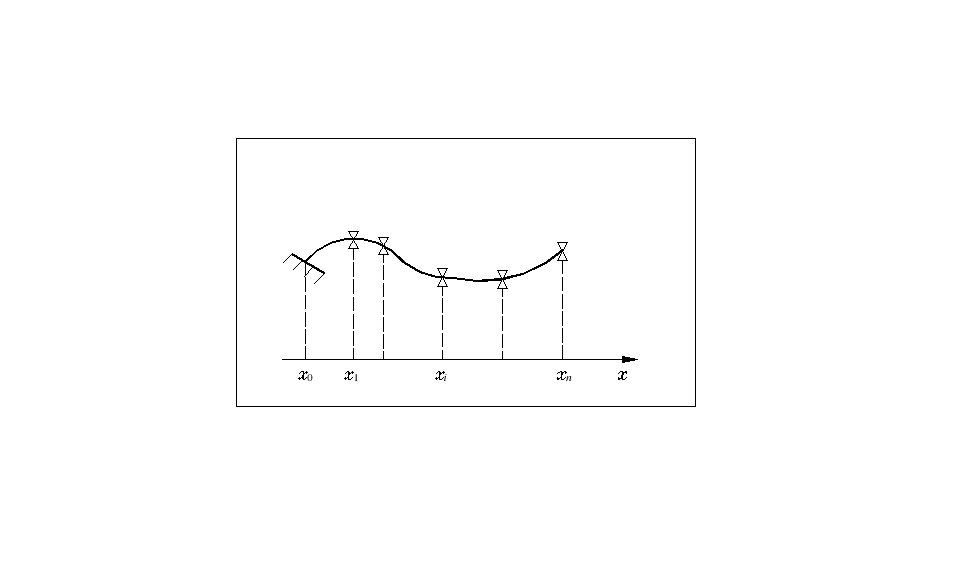
Rys. 4.12

Równanie linii ugięcia giętki opisuje wzór Bernoulliego-Eulera [18]:

(4.51)

gdzie ρ jest promieniem krzywizny, - momentem gnącym,
- modułem Younga,
- geometrycznym momentem bezwładności.

Wzór (4.51) dotyczy wybranego przekroju giętki, wszystkie występujące wielkości są więc funkcjami jej długości.

Porównując wzór (4.51) ze wzorem na krzywiznę linii określonej równaniem
otrzymamy

(4.52)

Uzyskanego równania giętki nie można, niestety, rozwiązać w sposób efektywny i dlatego zachodzi potrzeba dokonania pewnych uproszczeń. Zakładając, że

(4.53)

oraz stałą sztywność uprościmy równanie (4.52) do postaci

(4.54)

gdzie

(4.55)

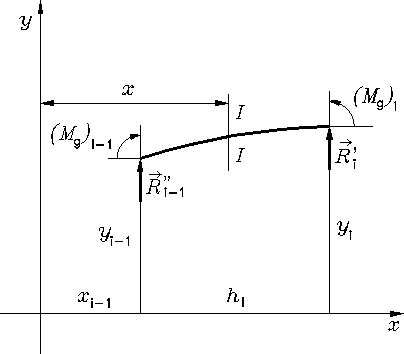
Rys. 4.13

Rozpatrując, przy założeniu (4.53), równowagę elementu giętki znajdującego się między punktami (rys. 4.13) wyznaczamy

(4.56)

Z kolei dla elementu znajdującego się między punktem
a przekrojem
jest

(4.57)

Z połączenia zależności (4.56) i (4.57), po wykorzystaniu (4.54) i (4.55), otrzymamy wzór

(4.58)

będący podstawowym równaniem wielomianowej funkcji sklejanej trzeciego stopnia - pierwszej funkcji sklejanej, przedstawionej matematycznemu światu przez I.J. Schoenberga w 1946 roku.

W odróżnieniu od interpolacyjnych wielomianów Lagrange'a, zwiększając liczbę węzłów
otrzymujemy funkcje sklejane coraz lepiej interpolujące zadaną funkcję
Ponadto okazało się, że optymalne - w sensie różnych kryteriów - rozwiązania wielu zadań są wyznaczane przez funkcje sklejane. Własności te spowodowały, że funkcje sklejane stały się po roku 1946 obiektem aktywnego zainteresowania matematyków.

Jedna z tych własności, zwana własnością minimalnej normy (ściśle związana
z minimalizacją energii potencjalnej, zużytej na odkształcenie giętki), wynika z następującego twierdzenia:

Twierdzenie Holladay'a [19]:

Niech będzie dana siatka i liczby rzeczywiste Spośród wszystkich funkcji mających na
ciągłą drugą pochodną i takich, że funkcja sklejana trzeciego stopnia z węzłami w dla której minimalizuje całkę

(4.59)

Ta ekstremalna własność funkcji sklejanej trzeciego stopnia została wykazana również dla wielomianowych funkcji sklejanych innych stopni. Rozpatrując jednak takie uogólnienie nie można mówić o własności minimalnej krzywizny - własność ta nazwana jest więc własnością minimalnej normy. Jest to w pełni możliwe, gdyż w każdym przypadku można rozpatrywać odpowiednią przestrzeń Hilberta, w której całka (4.59), lub jej analogon, jest równa kwadratowi funkcji

*

W celu ogólnego zdefiniowania funkcji sklejanej na siatce (4.1)

(4.60)

oznaczymy przez zbiór wielomianów stopnia nie przewyższającego
, a przez zbiór takich funkcji, które mają na
ciągłe i ograniczone pochodne aż do rzędu
 włącznie.

Wielomianową funkcją sklejaną stopnia m z defektem
dla węzłów (4.60) nazywamy taką funkcję

(4.61)

która spełnia warunki:

Punkty nazywane są węzłami funkcji sklejanej, a sama funkcja może mieć nieciągłą pochodną rzędu

Oprócz tak zdefiniowanej wielomianowej funkcji sklejanej, czasami wygodnie jest wykorzystywać funkcje sklejane mające różną gładkość w różnych węzłach siatki - mogą one mieć zastosowanie przy aproksymacji takich funkcji, których gład-kość jest różna w różnych częściach przedziału

Pełne określenie funkcji sklejanej (4.61) nie wynika jeszcze z przedstawionej definicji. Mianowicie, mamy do wyznaczenia
współczynników, a tylko
warunków (warunki ciągłości funkcji i jej pochodnych w węzłach
. Niezdefiniowana pozostaje więc jeszcze pewna liczba parametrów, równa

(4.62)

Parametry te można wyznaczyć, jeśli znane są wartości funkcji w węzłach oraz pewne warunki nakładane na funkcję sklejaną w punktach a i b, zwane warunkami brzegowymi lub granicznymi - w tym przypadku mówimy o interpolującej (interpola-cyjnej) funkcji sklejanej. Nieznane parametry mogą być też wyznaczone z warunków minimalizacji określonych funkcjonałów, gdyż zgodnie z własnością minimalnej normy funkcje sklejane pozwalają na uzyskanie najlepszego przybliżenia, spośród wszystkich funkcji określonej klasy. Otrzymane w ten sposób funkcje sklejane noszą nazwę wygładzających (aproksymacyjnych) funkcji sklejanych.

Oprócz podziału wielomianowych funkcji sklejanych na interpolacyjne i aproksymacyjne należy jeszcze rozróżnić funkcje stopnia parzystego i funkcje stopnia nieparzystego. Okazuje się bowiem, że w przypadku funkcji sklejanych stopnia parzystego liczba nieznanych parametrów (4.62) nie zezwala na spełnienie wszystkich warunków - punkty sklejenia są z tego powodu na ogół różne od węzłów funkcji sklejanej.

Najprostszymi przykładami wielomianowych funkcji sklejanych jest funkcja - „kawałkami stała”, oraz funkcja - „kawałkami liniowa”.

Równanie interpolacyjnej funkcji sklejanej pierwszego stopnia można łatwo wyznaczyć uwzględniając warunki (4.3)

(4.63)

gdzie Funkcja ta należy do grupy tzw. lokalnych funkcji sklejanych, tzn. takich funkcji sklejanych, których parametry są rozwiązaniami układów równań, składających się z podukładów równań o niewielkich rozmiarach.

Pewne niedostatki zastosowania wielomianowych funkcji sklejanych związane są z możliwością pojawiania się niekontrolowanych punktów przegięcia (fałszywych oscylacji funkcji sklejanej) oraz z niemożnością przybliżania funkcji mających
w niektórych punktach styczne pionowe.

Wyeliminowanie ewentualnych oscylacji wielomianowej funkcji sklejanej trzeciego stopnia można uzyskać przy wykorzystaniu funkcji sklejanej, której równania wynikają z analizy równowagi elementu linii elastycznej rozciąganej dodatkowo sta-łą siłą
Z rysunku 4.14 - przy założeniu (4.53) - otrzymujemy

(4.64)

Rys. 4.14

Rys. 4.15

Z kolei dla elementu przedstawionego na rysunku 4.15 jest

(4.65)

Wykorzystując (4.54), (4.55) i (4.64) oraz wprowadzając oznaczenie

(4.66)

192 4. Interpolacja

4.7. Podstawowe pojęcia teorii funkcji sklejanych 197

---