93 9.3000E-0001 6.9634657E-0003 9.4382E-0004

94 9.4000E-0001 5.9483989E-0003 1.3611E-0003

95 9.5000E-0001 4.9826978E-0003 1.7727E-0003

96 9.6000E-0001 4.1317740E-0003 2.1101E-0003

97 9.7000E-0001 3.4940266E-0003 2.2721E-0003

98 9.8000E-0001 3.2098605E-0003 2.1157E-0003

99 9.9000E-0001 3.4723825E-0003 1.4452E-0003

100 1.0000E+0000 4.5399930E-0003 0.0000E+0000

4.3. Interpolacja Newtona

Interpolacja Newtona jest oparta na przyjęciu jako układu funkcji liniowo-niezależnych wielomianów czynnikowych postaci:

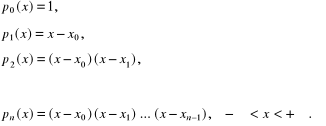
(4.21)

Po podstawieniu tej bazy do (4.8) otrzymujemy układ równań z trójkątną macierzą charakterystyczną:

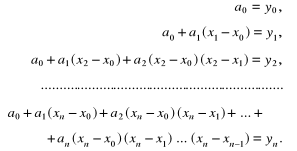
(4.22)

Przed rozwiązaniem tego układu równań niezbędne jest wprowadzenie pojęcia ilorazów różnicowych. Dla funkcji
określonej na dyskretnym zbiorze argumentów (4.3) definiujemy ilorazy różnicowe pierwszego rzędu:

(4.23)

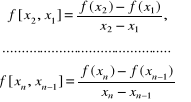
(4.23cd.)

oraz rekurencyjnie ilorazy różnicowe rzędu k

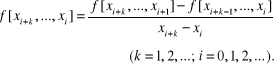
(4.24)

Obliczanie powyższych ilorazów różnicowych można wykonać w łatwiejszy sposób przy wykorzystaniu zależności

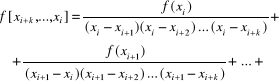
(4.25)

lub posługując się następującą tablicą ilorazów różnicowych:

	xi	Yi	Ilorazy różnicowe
	x0	Y0
	x1	Y1
	x2	Y2
	x3	Y3
	...	...

Przykładowo dla wielomianu trzeciego stopnia dla węzłów interpolacji: tablica ilorazów różnicowych ma postać:

	xi	Yi	Ilorazy różnicowe
	0	0
			4
	2	8		5
			19		1
	3	27		10		0
			49		1
	5	125		14
			91
	6	216

Rozwiązując kolejne równania układu równań (4.22) otrzymujemy:

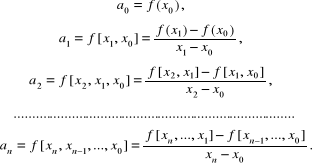
(4.26)

Tak więc wzór interpolacyjny Newtona ma postać:

(4.27)

Współczynniki   wielomianu interpolacyjnego Newtona

(4.28)

można wyznaczyć również w inny sposób, wykorzystując zależność rekurencyjną

Wielomiany mają współczynnik równy jedności przy zatem współczynnik jest równy współczynnikowi przy w wielomianie interpolacyjnym Lagrange'a

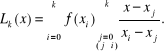
Stąd oraz na mocy związku (4.25) jest

Przykład. Znaleźć wielomian interpolacyjny Newtona, który w punktach: 0, 2,
3, 5 przyjmuje wartości: 1, 3, 2, 5.

Sporządzamy najpierw tablicę ilorazów różnicowych:

	xi	Yi	ilorazy różnicowe
	0	1
			1
	2	3		−2/3
			−1		3/10
	3	2		5/6
			3/2
	5	5

i następnie otrzymujemy

*

W przypadku węzłów równoodległych ilorazy różnicowe kolejnych rzędów wy-noszą odpowiednio:

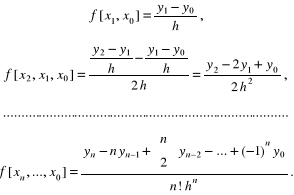
Można je zapisać w szczególnie wygodny sposób za pomocą skończonych różnic progresywnych funkcji
zdefiniowanych następująco:

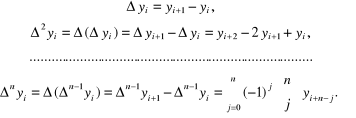
(4.29)

Korzystając z tych wzorów po podstawieniu do (4.27) otrzymujemy wzór interpolacyjny Newtona dla węzłów równoodległych

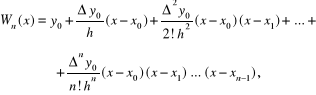
który łatwiej jest stosować po wprowadzeniu pomocniczej zmiennej (4.18)

(4.30)

Operator różnicowania
ma wiele własności podobnych do własności operatora różniczkowego:

Łatwo ponadto można wykazać, że w przypadku wielomianu n-tego stopnia n-ta różnica jest stała i ma postać

Obliczone różnice kolejnych rzędów najwygodniej jest układać w postaci trójkątnej tablicy różnic progresywnych:

	xi	yi
	x0	y0
	x1	y1
	x2	y2
	x3	y3

Wzory interpolacyjne (4.27) i (4.31), zwane pierwszymi wzorami interpolacyjnymi, są stosowane do interpolacji funkcji
w otoczeniu wartości początkowej Do interpolacji funkcji
w pobliżu końca tablicy wygodniej jest wykorzystywać tzw. drugie wielomiany interpolacyjne Newtona postaci

których współczynniki określane są za pomocą wstecznych ilorazów różnicowych

lub też wstecznych różnic skończonych

Dla węzłów równoodległych, po podstawieniu

analogicznym do (4.18), otrzymamy

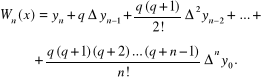
(4.31)

Ze względu na możliwość nieuwzględniania we wzorach interpolacyjnych New-tona tych składników, których współczynniki są dostatecznie małe, mogą one okazać się korzystniejsze w stosowaniu niż wielomian interpolacyjny Lagrange'a, w którym każdy ze składników jest jednakowo istotny i nie można żadnego z nich zaniedbać.

{Program 4.2}

unit Obliczenia;

interface

uses

Windows, Messages, SysUtils, Classes, Graphics, Controls,

Forms, Dialogs, StdCtrls, Buttons;

type

Tabl1 = array[0..100] of Real;

Tabl2 = array[1..1000] of Real;

. . . . . . . . . . . . . . . . .

var

Form3: TForm3;

i,j,K,n,m,wzor,X0,Y0,ZX,ZY: Integer;

xx,yy,Xekr,Yekr: Tabl2;

a,b,bl,h,x,y: Real;

plik,plik1: Text;

xw,yw: Tabl1;

implementation

uses Ustawienia, Informacje, Grafika, Podglad;

{$R *.DFM}

function f(x: Real): Real;

begin

f:=100*x*x*Exp(-10*x);

end;

procedure Newton(wzor,n: Integer; x: Real; var y: Real;

xw,yw: Tabl1);

var

k,l: Integer;

f: Tabl1;

begin

f:=yw;

case wzor of

1: for k:=1 to n do

for l:=n downto k do

f[l]:=(f[l]-f[l-1])/(xw[l]-xw[l-k]);

2: for k:=n-1 downto 0 do

for l:=0 to k do

f[l]:=(f[l+1]-f[l])/(xw[n+l-k]-xw[l]);

end;

if wzor=1 then begin

y:=f[n];

for k:=n-1 downto 0 do

y:=y*(x-xw[k])+f[k];

end else begin

y:=f[0];

for k:=1 to n do

y:=y*(x-xw[k])+f[k];

end;

end;

. . . . . . . . . . . . . . . . . . . . . .

procedure TForm3.BitBtn1Click(Sender: TObject);

begin

Form2.Show;

if RadioButton1.Checked then wzor:=1;

if RadioButton2.Checked then wzor:=2;

a:=StrToFloat(Edit1.Text); b:=StrToFloat(Edit2.Text);

n:=StrToInt(Edit3.Text); m:=StrToInt(Edit4.Text);

AssignFile(plik,Edit6.Text); AssignFile(plik1,Edit5.Text);

Rewrite(plik); Rewrite(plik1);

Writeln(plik,'Program 4.2.');

Writeln(plik,'Interpolacja funkcji jednej zmiennej.');

case wzor of

1: Writeln(plik,'Pierwszy wzór interpolacyjny Newtona.');

2: Writeln(plik,'Drugi wzór interpolacyjny Newtona.');

end;

Writeln(plik);

Writeln(plik,'Początek przedziału: a = ',a:13);

Writeln(plik,'Koniec przedziału: b = ',b:13);

Writeln(plik,'Liczba węzłów: n = ',n:3);

Writeln(plik,'Liczba punktów wykresu: m = ',m:3);

Writeln(plik1,n:3); Writeln(plik1,m:3);

Writeln(plik);

h:=(b-a)/n;

for i:=0 to n do begin

x:=a+i*h; y:=f(x);

xw[i]:=x; yw[i]:=y;

xx[i+1]:=x; yy[i+1]:=y;

end;

xx[n+2]:=0; yy[n+2]:=0; K:=n+2;

Writeln(plik,'Wyniki interpolacji funkcji:');

Writeln(plik,' i x[i] y[i] błąd');

h:=(b-a)/m;

for i:=0 to m do begin

x:=a+i*h;

Newton(wzor,n,x,y,xw,yw); bl:=f(x)-y;

Writeln(plik,i:3,' ',x:13,' ',y:16,' ',bl:13);

K:=K+1; xx[K]:=x; yy[K]:=y;

end;

for i:=1 to m+n+3 do

Writeln(plik1,xx[i]:13,' ',yy[i]:13);

CloseFile(plik); CloseFile(plik1);

Form2.Wyniki.Lines.LoadFromFile(Edit6.Text);

end;

. . . . . . . . . . . . . . . . . . . . . . .

procedure TForm3.BitBtn3Click(Sender: TObject);

begin

Close;

end;

end.

Rys. 4.2

Program 4.2 jest zmodyfikowanym programem 4.1 przeznaczonym do interpolowania funkcji
za pomocą wielomianów interpolacyjnych Newtona. W programie tym najpierw obliczane są ilorazy różnicowe, a następnie w zależności od wyboru alternatywy obliczeń na formularzu Dane (rys. 4.2) wyznaczane są wartości funkcji w m równoległych punktach, przy wykorzystaniu albo pierwszego lub też drugiego wzoru interpolacyjnego Newtona.

Rozwiązując dwukrotnie to samo zadanie, które było rozważane przy testowaniu działania programu 4.1 otrzymujemy wyniki przedstawione na rysunku 4.1 oraz stanowiące załączone fragmenty wydruków komputerowych.

PROGRAM 4.2.

Interpolacja funkcji jednej zmiennej.

Pierwszy wzór interpolacyjny Newtona.

Początek przedziału: a = 0.0000E+0000

Koniec przedziału: b = 1.0000E+0000

Liczba węzłów: n = 10

Liczba punktów wykresu: m = 100

Wyniki interpolacji funkcji:

i x[i] y[i] błąd

0 0.0000E+0000 0.0000000E+0000 0.0000E+0000

1 1.0000E-0002 1.3360847E-0002 -4.3125E-0003

2 2.0000E-0002 3.8910743E-0002 -6.1615E-0003

3 3.0000E-0002 7.3132626E-0002 -6.4590E-0003

4 4.0000E-0002 1.1310700E-0001 -5.8558E-0003

5 5.0000E-0002 1.5643571E-0001 -4.8030E-0003

6 6.0000E-0002 2.0117326E-0001 -3.6011E-0003

7 7.0000E-0002 2.4576536E-0001 -2.4386E-0003

8 8.0000E-0002 2.8899388E-0001 -1.4233E-0003

9 9.0000E-0002 3.2992775E-0001 -6.0633E-0004

10 1.0000E-0001 3.6787944E-0001 0.0000E+0000

. . . . . . . . . . . . . . . . . . . . . . . . . .

PROGRAM 4.2.

Interpolacja funkcji jednej zmiennej.

Drugi wzór interpolacyjny Newtona.

. . . . . . . . . . . . . . . . . .

Wyniki interpolacji funkcji:

i x[i] y[i] błąd

0 0.0000E+0000 1.6271429E-0012 -1.6271E-0012

1 1.0000E-0002 1.3360847E-0002 -4.3125E-0003

2 2.0000E-0002 3.8910743E-0002 -6.1615E-0003

3 3.0000E-0002 7.3132626E-0002 -6.4590E-0003

4 4.0000E-0002 1.1310700E-0001 -5.8558E-0003

5 5.0000E-0002 1.5643571E-0001 -4.8030E-0003

6 6.0000E-0002 2.0117326E-0001 -3.6011E-0003

7 7.0000E-0002 2.4576536E-0001 -2.4386E-0003

8 8.0000E-0002 2.8899388E-0001 -1.4233E-0003

9 9.0000E-0002 3.2992775E-0001 -6.0633E-0004

10 1.0000E-0001 3.6787944E-0001 -9.0949E-0013

. . . . . . . . . . . . . . . . . . . . . . . . . .

176 4. Interpolacja

4.3. Interpolacja Newtona 175

---