Tomasz Pajączkowski

21.03.2001

Ćwiczenie nr 7.

Temat: Żyroskop.

Celem ćwiczenia jest wyznaczenie momentu bezwładności tarczy żyroskopu oraz sprawdzenie równań precesji.

Tabela wyników:

	dla Δr = 0,02 m							dla Δr = -0,02 m
	t [ s ]		ε [ s ]				ε² [ s² ]	t [ s ]		ε [ s ]				ε² [ s² ]
1	21,118		-0,755				0,57	21,373		1,008				1,016
2	20,811		-1,062				1,128	20,177		-0,188				0,035
3	19,490		-2,383				5,679	21,816		1,451				2,105
4	22,522		0,649				0,421	22,261		1,896				3,595
5	23,558		1,685				2,839	19,194		-1,171				1,371
6	23,019		1,146				1,313	19,217		-1,148				1,318
7	21,889		0,016				0,00026	19,430		-0,935				0,874
8	22,374		0,501				0,251	19,297		-1,068				1,141
9	23,515		1,642				2,696	22,169		1,804				3,254
10	20,431		-1,442				2,079	19,883		-0,482				0,232
11								19,200		-1,165				1,357
		średni czas					Σ ε² [ s² ]		średni czas					Σ ε² [ s² ]
	Σ 218,727	21,8727 s					16,97626	Σ 224,017	20,3652 s						16,298

Teoria zjawiska:

Ruch bryły sztywnej może się składać z ruchu postępowego i ruchu obrotowego. W ruchu postępowym bryła może być uważana za punkt materialny, gdyż wszystkie jej części poruszają się w taki sam sposób. Fakt ten pozwala stosować przy dynamicznym opisie ruchu postępowego bryły sztywnej zasady dynamiki dla punktu materialnego. Zasady dynamiki dla ruchu obrotowego sformułowane zostały poniżej, gdyż inne wielkości dynamiczne decydują o charakterze i przebiegu tego ruchu. Wielkości tymi są: moment siły -jest wielkością wektorowa równa iloczynowi wektorowemu wektora położenia punktu przyłożenia siły i wektora siły działającej na bryłę ( M = r x F ). Zgodnie z definicją iloczynu wektorowego powyższy wzór ma postać: M = r sinφ F.

Kolejną wielkością dynamiczną związaną z ruch obrotowy bryły sztywnej jest moment pędu. Moment pędu bryły równa się iloczynowi jej prędkości kątowej ω i momentowi bezwładności I ( L = I ω ). Momentem bezwładności I względem danej osi nazywamy sumę iloczynów mas poszczególnych punktów i kwadratu ich odległości od danej osi ( I = Σ m_ir² ).

W związku z powyższym zasady dynamiki dla ruchu obrotowego mają następującą postać:

Pierwsza zasada dynamiki ruchu obrotowego:

Bryła sztywna nie poddana działaniu momentu siły pozostaje w spoczynku lub obraca się ruchem jednostajnym.

Druga zasada dynamiki ruchu obrotowego:

Przyrost momentu pędu bryły sztywnej jest równy popędowi momentu siły wywartej na bryłę ( Mdt = dL ).

Trzecia zasada dynamiki ruchu obrotowego:

Jeżeli bryła A działa na bryłę B pewnym momentem siły M_AB, to bryła B działa na bryłę A równym co do wartości, kierunku lecz przeciwnie skierowanym momentem siły -M_BA.

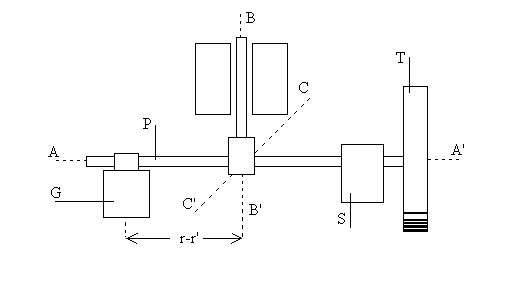
Żyroskopem nazywamy bryłę sztywną osadzoną na osi będącej równocześnie swobodną osią obrotu i osią największego momentu bezwładności. Oś obrotu AA' żyroskopu może obracać się wokół dwóch innych osi: BB' oraz CC' ( co pokazano na rysunku poniżej ).

Bryłą sztywną jest mosiężna tarcza T, napędzana lekkim silnikiem elektrycznym S. Pręt P, na którym osadzony jest silnik z tarczą, jest podparty powyżej środka ciężkości i stanowi dźwignię dwustronną, na której ciężar tarczy równoważy ciężarek G o masie m.

Ruchem żyroskopu rządzą zasady dynamiki bryły sztywnej. Zgodnie z drugą zasadą dynamiki ( Mdt = dL ) moment siły jest pochodną momentu pędu L względem czasu M =dL/dt. W przypadku, gdy nie występuje moment siły ( M =0 ),powyższe równanie

przyjmuje postać dL/dt = 0, stąd wynika L = const. Ostatni związek stanowi treść zasady zachowania momentu pędu ( gdy na ciało nie działa moment siły lub działające momenty równoważą się, to wartość i kierunek momentu pędu pozostają stałe ). Ponieważ wartość momentu wyraża się wzorem L =I ω zatem zasadę zachowania momentu pędu można przedstawić w postaci Iω =const.

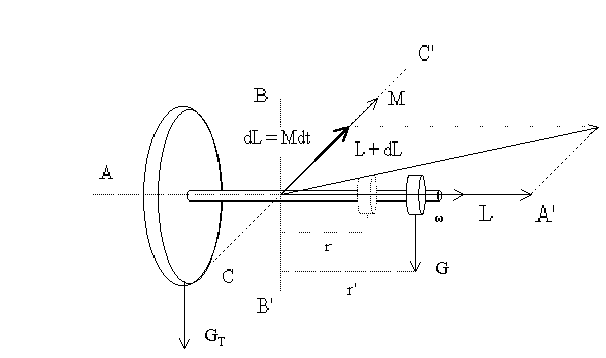
Wynika stąd, że gdy na bryłę nie działa moment siły ( M=0 ), a jej moment bezwładności I jest stały, prędkość kontowa musi być stała. Siła leżąca na lini przechodzącej przez środek masy bryły wywołuje ruch postępowy zgodnie z II zasadą dynamiki ( F = ma ). Stąd też żyroskop zachowuje stałą prędkość kontową i oś.

Gdy na żyroskop działa moment M równoległy do osi CC' (co pokazano na rysunku powyżej ) jego moment pędu L w dowolnie małym odcinku czasu dt wzrasta o dL. Wektor dL jest więc równoległy do wektora M, a prostopadły do L. Nie zmienia on wartości wektora L, lecz jego kierunek. Ponieważ moment siły działa w sposób ciągły, w sposób ciągły zmienia się również kierunek całkowitego momentu pędu L. Ze względu na stałość I prędkość kontowa zmienia się w taki sam sposób jak moment pędu, stąd cały żyroskop obraca się wokół osi BB'. Taki obrót żyroskopu pod wpływem zewnętrznego momentu pędu nazywamy precesją. W przypadku, gdy moment siły M jest równoległy do osi CC', to moment pędu L zmienia swój kierunek w sposób ciągły a jego koniec zatacza koło o promieniu L.

Opis metody z opisem przeprowadzonego eksperymentu:

Żyroskop pomiarowy stosowany w ćwiczeniu posiadał tachometr prędkości obrotowej żyroskopu oraz układ fotoelektryczny wskazujący kąt precesji. Jest on również zaopatrzony w analogowy miernik częstotliwości obrotów silnika.

Tak więc cały pomiar sprowadzał się do odczytania wartości wskazań tachometru przy obrocie żyroskopu o pewną wartość kąta ( w tym przypadku pomiaru dokonywałem dla wartości 30° co po przeliczeniu na jednostki SI daje 1/6·π rad ) przy stałej wartości prędkości kątowej silnika ( ω = 2πf ).

Pomiar powtórzyłem dziesięciokrotnie dla obciążnika przesuniętego w pozycję oddaloną o 2 cm od pozycji równowagi, oraz o -2 cm od pozycji równowagi. Otrzymane wartości zebrałem w powyższej tabeli, a następnie na ich podstawie dokonałem obliczeń i wyciągnąłem końcowe wnioski.

Wzory robocze:

Z definicji pochodnej, dla skalarnej wartości momentu pędu L otrzymujemy następujący związek: dL/dt = lim ΔL/Δt = lim (łuk zakreślony przez wektor L)/Δt =lim LΔβ/Δd = L·dβ/dt zatem dL/dt = Lω_P ,gdzie ω_P = dβ/dt -prędkość kontowa precesji. Z poprzedniego wynika następująca zależność: M = Lω_P co po uwzględnieniu zależności L=I x ω daje: M =Iω_P x ω. W przypadku, gdy występujące w powyższym równaniu wektory M, ω_P, ω pozostają zawsze wzajemnie prostopadłe ( z czym mamy do czynienia w przypadku żyroskopu ) związek ten można zapisać w postaci skalarnej.

Na żyroskop działają zawsze dwa momenty siły: M _tarczy i M _ciężarka. Gdy są one zrównoważone ( M _tarczy +M _ciężarka =M =0 ), precesja nie występuje ( ω_P =0 ). Gdy ciężarek przesuniemy z pozycji r w pozycję r' ( co przedstawione zostało na powyższym rysunku ) wówczas M = (r - r' )mg .W tym przypadku wartość ω_P jest różna od zera, co skutkuje tym, że żyroskop doznaje zjawiska precesji. Wówczas wzór na moment siły ma postać:

M | r - r' |mg = I ω_Pω

Przekształcając powyższe równanie otrzymujemy zależność na I :

I =| r - r' |mg/ω_Pω

Obliczenia do wykonanego ćwiczenia:

Obliczenia wartości ω i ω_P dla uśrednionej wartości t.

1) ω_P = β/t = (π/6)/21,8727 = 0,0239 1/s

ω = 2πf = 2·3,14159·66,66667 = 418,879 1/s

I = Δrmg/ω_pω =(0,02·0,375·9,81)/ (0,0239·418,879) = 0,007349 kg·m²

2) ω_P = β/t = (π/6)/20,3652 = 0,0257 1/s

ω = 2πf = 2·3,14159·66,66667 = 418,879 1/s

I = Δrmg/ω_pω =( 0,02·0,375·9,81)/ (0,0257·418,879) = 0,006835 kg·m²

{ Działania na jednostkach: [ I = (m·kg·m/s²)/ (1/s·1/s) = kg·m² ]}

Szacowanie niepewności pomiaru dla wyznaczonych wartości ω i ω_P:

1. U_A(t) = [ Σε²/n(n-1) ]^1/2 = [ 16,977/90 ]^1/2 = 0,434 s

U_B(t) = 0,001/ 3^1/2 = 0,00058 s

Uc(t) = 0,434 s

Zatem dla powyższego możemy wyznaczyć przybliżenie z jakim podana została wartość ω_P.

U_A(ω_P) = β/t²·U_C(t) = 4,71·10^-4 1/s

Dla ω niepewność wyznaczam z zależności: U_A(ω) = (50/60s)/3^1/2 = 0,23 1/s

2. U_A(t) = [ Σε²/n(n-1) ]^1/2 = [ 16,298/110 ]^1/2 = 0,385 s

U_B(t) = 0,001/ 3^1/2 = 0,00058 s

Uc(t) = 0,385 s

Zatem dla powyższego możemy wyznaczyć przybliżenie z jakim podana została wartość ω_P.

U_A(ω_P) = β/t²·U_C(t) = 4,02·10^-4 1/s

Dla ω niepewność wyznaczam z zależności: U_A(ω) = (50/60s)/3^1/2 = 0,23 1/s

Szacowanie niepewności pomiaru:

1. [ U_B(g) = 0,01/ 3^1/2 = 0,0058 m/s² ]² = 3,36·10^-7 m/s⁴

[ U_B(Δr) = 0,01/ 3^1/2 = 0,0058 m ]² = 3,36·10^-5 m²

2. [ U_B(g) = 0,01/ 3^1/2 = 0,0058 m/s² ]² = 3,36·10^-7m²/s⁴

[ U_B(Δr) = 0,01/ 3^1/2 = 0,0058 m ]² = 3,36·10^-5 m²

W obydwóch powyższych przypadkach wartości UB(ωp) i UB (ω) są bardzo małe dlatego można przyjąć, że UC dla tych przypadków = UA.

1) [ ðI/ðΔr = mg/ω_pω = 0,3675 kg·m ]² = 0,135 kg²·m²

[ ðI/ðm = Δrg/ω_pω = 0,0196 m² ]² = 3,8·10^-4 m⁴

[ ðI/ðg = Δrm/ω_pω = 0,0007 kg·m/s² ]² = 4,9·10^-7 kg²·m²/s⁴

[ ðI/ðω_p = -Δrmg/ωp²ω = -0,3075 kg·m²/s ]² = 0,095 kg²·m⁴/s²

[ ðI/ðω = -Δrmg/ω_pω² = -1,75·10^-5 kg·m²/s ]² = 3,06·10^-10 kg²·m⁴/s²

2) [ ðI/ðΔr = mg/ω_pω = -0,3417 kg·m ]² = 0,11675889 kg²·m²

[ ðI/ðm = Δrg/ω_pω = -0,0182 m² ]² = 0,00033124 m⁴

[ ðI/ðg = Δrm/ω_pω = -0,0007 kg·m/s² ]² = 4,9·10^-7 kg²·m²/s⁴

[ ðI/ðω_p = -Δrmg/ωp²ω = 0,2659 kg·m²/s ]² = 0,071 kg²·m⁴/s²

[ ðI/ðω = -Δrmg/ω_pω² = 1,6·10^-5 kg²·m⁴/s²]² =2,56·10^-10 kg²·m⁴/s²

U(I) = [ (ðI/ðΔr)²U²(Δr)+ (ðI/ðm)²U²(m)+ (ðI/ðg)²U²(g)+ (ðI/ðω_P)²U²(ω_P)+ (ðI/ðω)²U²(ω) ]^1/2=

Po podstawieniu do powyższego wzoru wyznaczonych powyżej wartości otrzymujemy:

1. = 2,59·10^-4 kg·m²

2. = 4,93·10^-4 kg·m²

α =0,95 U_C(I) = 2 U(I)

1) U_C(I) = 0,518·10^-3 kg·m²

^{2) UC(I) = 0,99·10-3 kg·m²}

{ Działanie na jednostkach: [ ( U_C(I) = [(kg·m/s²)/ (1/s²)]²m²+ [(m²/s²)/ (1/s²)]²kg²+[(m·kg)/ (1/s²)]²m²/s⁴+[(m·kg·m/s²)/ /(1/s)]²·1/s²+[ (m·kg·m/s²)/ (1/s)]²1/s²]^1/2 = [kg²·m⁴]^1/2= kg·m²]] }

Ostatecznie wartość momentu bezwładności tarczy żyroskopu wynosi:

1. I = ( 7,349 ± 0,518 ) ·10^-3 kg·m²

2. I = ( 6,835 ± 0,99 ) ·10^-3 kg·m²

Wyznaczanie średniej wartości I dla powyższego:

^{Iśr = ( I1 + I2 )/2 = 7,05·10-3 kg·m²}

U_C(I_śr) = 0,5·[ U_C(I₁) + U_C(I₂)]^1/2 = 5,59·10^-4 kg·m²

I = ( 7,05 ± 0,56 )·10-3 kg·m²

Wnioski:

Wyznaczony moment bezwładności wynosi: I = ( 7,05 ± 0,56 )·10^-3 kg·m².

Ewentualne błędy przy wyznaczaniu powyższej wartości wynikać mogą z dużej czułości aparatury, która to mogła skutkować tym, że przy nieznacznych zmianach parametrów wykonywanego doświadczenia ( tj. np. niewielkich spadków prędkości obrotów silnika ) wystąpić mogły znaczne różnice w czasie precesji żyroskopu.

Również niemałe znaczenie ma w tym przypadku siła tarcia. Powoduje ona opóźnienie ruchu precesji żyroskopu, co skutkuje niedokładnością pomiaru.

α = 30°

f = 4000 obr./min.

m = 375 g

---