2 -9.6000E-0001 4.1593883E-0002 3.4544E-0006

3 -9.4000E-0001 4.3306178E-0002 2.6138E-0006

4 -9.2000E-0001 4.5125086E-0002 1.2675E-0006

5 -9.0000E-0001 4.7058824E-0002 -5.6843E-0014

6 -8.8000E-0001 4.9116754E-0002 -8.4072E-0007

7 -8.6000E-0001 5.1309486E-0002 -1.1226E-0006

8 -8.4000E-0001 5.3648975E-0002 -9.0615E-0007

9 -8.2000E-0001 5.6148647E-0002 -4.1518E-0007

10 -8.0000E-0001 5.8823529E-0002 0.0000E+0000

11 -7.8000E-0001 6.1690302E-0002 1.2726E-0008

12 -7.6000E-0001 6.4767148E-0002 -3.0835E-0007

13 -7.4000E-0001 6.8074249E-0002 -7.3004E-0007

14 -7.2000E-0001 7.1634094E-0002 -8.5623E-0007

15 -7.0000E-0001 7.5471698E-0002 0.0000E+0000

. . . . . . . . . . . . . . . . . . . . . . . . .

30 -4.0000E-0001 2.0000000E-0001 0.0000E+0000

31 -3.8000E-0001 2.1697951E-0001 -5.9772E-0005

32 -3.6000E-0001 2.3597006E-0001 -1.2100E-0004

33 -3.4000E-0001 2.5722845E-0001 -1.5904E-0004

34 -3.2000E-0001 2.8103420E-0001 -1.3532E-0004

35 -3.0000E-0001 3.0769231E-0001 0.0000E+0000

36 -2.8000E-0001 3.3756291E-0001 2.7493E-0004

37 -2.6000E-0001 3.7114464E-0001 6.0257E-0004

38 -2.4000E-0001 4.0899984E-0001 8.3622E-0004

39 -2.2000E-0001 4.5173365E-0001 7.5504E-0004

40 -2.0000E-0001 5.0000000E-0001 -9.0949E-0013

41 -1.8000E-0001 5.5410114E-0001 -1.6149E-0003

42 -1.6000E-0001 6.1276852E-0001 -3.0124E-0003

43 -1.4000E-0001 6.7437225E-0001 -3.2313E-0003

44 -1.2000E-0001 7.3731180E-0001 -2.0177E-0003

45 -1.0000E-0001 8.0000000E-0001 -9.0949E-0013

46 -8.0000E-0002 8.6042787E-0001 1.6411E-0003

47 -6.0000E-0002 9.1488571E-0001 2.5455E-0003

48 -4.0000E-0002 9.5918474E-0001 2.3537E-0003

49 -2.0000E-0002 9.8903452E-0001 1.0644E-0003

50 5.1159E-0013 1.0000000E+0000 1.8190E-0012

. . . . . . . . . . . . . . . . . . . . . . . . .

4.11. Interpolacja funkcji dwóch zmiennych

Wszystkie przedstawione w rozdziałach 4.2 ÷ 4.6 metody interpolacji funkcji jednej zmiennej mogą być formalnie rozszerzone na przypadek funkcji n zmiennych niezależnych opierając się na zasadzie uzmienniania stałych współczynników występujących w poszczególnych funkcjach jednej zmiennej niezależnej. Oznacza to tym samym, że w każdym przekroju, w którym zmiennych niezależnych ma stałe wartości funkcja interpolująca jest funkcją jednej zmiennej niezależnej, a baza interpolacyjna dla funkcji wielu zmiennych niezależnych jest iloczynem tensorowym odpowiednich baz rozważanych przy interpolacji funkcji jednej zmiennej niezależnej.

Najbardziej użyteczne i najczęściej stosowane metody interpolacji funkcji wielu zmiennych są oparte na wykorzystaniu wielomianowych funkcji sklejanych uogólnionych na większą liczbę zmiennych niezależnych - ze względu na przedstawione problemy związane ze zbieżnością interpolacji wielomianowej i trygonometrycznej oraz ich wadą jaką jest czułość na wybór węzłów interpolacyjnych. Zapewnia to zachowanie podstawowych własności funkcji sklejanych jednej zmiennej i zezwala na uzyskanie niezbyt skomplikowanych algorytmów.

Nasze rozważania ograniczymy do przedstawienia niektórych interpolacyjnych funkcji sklejanych dwóch zmiennych w obszarze prostokątnym
w którym zdefiniowano siatkę
gdzie:

(4.138)

dzielącą obszar na prostokątne komórki:

(4.139)

Przedstawienie funkcji dwóch zmiennych w obszarze prostokątnym (4.138) jest dostatecznie ogólne, gdyż większość powierzchni możemy sparametryzować wprowadzając dwie rodziny linii - takich, których początki i końce znajdują się w punktach leżących na przeciwległych brzegach rozważanego płata powierzchni.

Wielomianową funkcją sklejaną dwóch zmiennych stopnia z defektem k względem zmiennej x i stopnia
z defektem l
względem zmiennej z liniami sklejenia na siatce nazywamy taką funkcję

(4.140)

która:

1) należy do zbioru algebraicznych wielomianów stopnia nie wyższego od
względem zmiennej x i nie wyższego od
względem zmiennej y,

2) należy do przestrzeni funkcji
ciągłych na mających ciągłe pochodne cząstkowe rzędu względem zmiennej x i rzędu względem zmiennej y.

Zgodnie z podaną definicją dwuliniowa funkcja sklejana może być zapisana w każdej komórce (4.139) w postaci

(4.141)

Nieznane współczynniki we wzorze (4.141) wyznaczymy z przyjętych warunków interpolacji

(4.142)

Ponieważ przy ustalonej wartości jednej ze zmiennych
funkcja jest funkcją sklejaną względem drugiej z tych zmiennych, to wykorzystując wzór (4.63) możemy napisać

(4.143)

gdzie:

(4.144)

Interpolując ponownie obliczone funkcje i otrzymujemy

(4.145)

gdzie:

(4.146)

i ostatecznie po podstawieniu (4.143) do (4.145) jest

(4.147)

Biliniowa funkcja sklejana (4.147) została wykorzystana w programie 4.7, przeznaczonym do wykreślania wykresów warstwicowych funkcji dwóch zmiennych
określonej w sposób dyskretny na siatce (4.138). Dla wykreślenia wykresu funkcji niezbędne jest wyznaczenie najpierw jej wartości ekstremalnych w węzłach siatki oraz obliczenie przyrostu dla zadanej liczby podprzedziałów

Następnie w każdym oczku siatki (4.138) funkcja jest interpolowana funkcją sklejaną (4.147) i w zależności od tego czy liczba całkowita

jest liczbą parzystą, czy też nieparzystą - wyświetlanemu pikselowi przypisywany jest odpowiedni kolor. Linie z = const są więc liniami oddzielającymi obszary narysowane różnymi kolorami (w grafice czarno-białej liniami oddzielającymi obszary o różnym stopniu szarości).

{Program 4.7}

unit Rysunek;

interface

uses

Windows, Messages, SysUtils, Classes, Graphics, Controls,

Forms, Dialogs, StdCtrls, Buttons;

type

Tabl = array [0..375,0..375] of Real;

. . . . . . . . . . . . . . . . . . . .

var

Form6: TForm6;

a,b,del,h,max,min,pp,x,xp,y,yp,r,r1,Re,s,s1: Real;

i,i1,i2,ii,j,jj,K,n,n1,M,ZX,ZY: Integer;

xw,yw: array [1..4] of Real;

plik: Text;

fun: Tabl;

implementation

uses Grafika, Obliczenia;

{$R *.DFM}

procedure TForm6.FormCreate(Sender: TObject);

begin

zbior:=Form3.Edit1.Text;

end;

. . . . . . . . . . . . . . . . . . . . . . .

procedure TForm6.Button1Click(Sender: TObject);

begin

Form4.Show; Close;

AssignFile(plik,zbior);

Reset(plik);

Readln(plik,n);

for i:=0 to n do

for j:=0 to n do

Readln(plik,fun[i,j]);

CloseFile(plik); n1:=n-1;

ZX:=Form4.PaintBox1.Width div 2;

ZY:=Form4.PaintBox1.Height;

a:=ZY-50; b:=ZY/2;

xw[1]:=ZX-a/2; xw[2]:=ZX+a/2;

xw[3]:=xw[2]; xw[4]:=xw[1];

yw[1]:=b+a/2; yw[2]:=yw[1];

yw[3]:=b-a/2; yw[4]:=yw[3];

h:=a/n; M:=Round(h);

Form4.Image1.Canvas.Pen.Color:=clBlack;

Form4.PaintBox1.Canvas.Pen.Color:=clBlack;

Form4.PaintBox1.Canvas.Brush.Color:=clWhite;

min:=fun[0,0]; max:=fun[0,0];

for i:=0 to n do

for j:=0 to n do begin

pp:=fun[i,j];

if pp<min then min:=pp;

if pp>max then max:=pp;

end;

del:=(max-min)/20;

for j:=0 to n1 do begin

yp:=yw[1]-j*h;

for i:=0 to n1 do begin

xp:=xw[1]+i*h;

for jj:=0 to M do begin

s:=jj/h; s1:=1-s;

for ii:=0 to M do begin

r:=ii/h; r1:=1-r;

pp:=s1*(r1*fun[i,j]+r*fun[i+1,j])+

s*(r1*fun[i,j+1]+r*fun[i+1,j+1]);

K:=Trunc((pp-min)/del);

if Odd(K) then begin

Form4.PaintBox1.Canvas.Pixels[Round(xp+ii),

Round(yp-jj)]:=clRed;

Form4.Image1.Canvas.Pixels[Round(xp+ii),

Round(yp-jj)]:=clRed

end else begin

Form4.PaintBox1.Canvas.Pixels[Round(xp+ii),

Round(yp-jj)]:=clGreen;

Form4.Image1.Canvas.Pixels[Round(xp+ii),

Round(yp-jj)]:=clGreen;

end;

end;

end;

end;

end;

if Form3.CheckBox1.Checked then begin

for ii:=0 to 2*ZX do

for jj:=0 to ZY do begin

if (Form4.PaintBox1.Canvas.Pixels[ii,jj]=clGreen) and

(Form4.PaintBox1.Canvas.Pixels[ii,jj+1]=clRed) then

begin

Form4.PaintBox1.Canvas.Pixels[ii,jj+1]:=clBlack;

Form4.Image1.Canvas.Pixels[ii,jj+1]:=clBlack;

end;

end;

for ii:=0 to 2*ZX do

for jj:=0 to ZY do begin

if (Form4.PaintBox1.Canvas.Pixels[ii,jj]=clRed) and

(Form4.PaintBox1.Canvas.Pixels[ii,jj+1]=clGreen) then

begin

Form4.PaintBox1.Canvas.Pixels[ii,jj+1]:=clBlack;

Form4.Image1.Canvas.Pixels[ii,jj+1]:=clBlack;

end;

end;

for jj:=0 to ZY do

for ii:=0 to 2*ZX do begin

if (Form4.PaintBox1.Canvas.Pixels[ii,jj]=clGreen) and

(Form4.PaintBox1.Canvas.Pixels[ii+1,jj]=clRed) then

begin

Form4.PaintBox1.Canvas.Pixels[ii+1,jj]:=clBlack;

Form4.Image1.Canvas.Pixels[ii+1,jj]:=clBlack;

end;

end;

for jj:=0 to ZY do

for ii:=0 to 2*ZX do begin

if (Form4.PaintBox1.Canvas.Pixels[ii,jj]=clRed) and

(Form4.PaintBox1.Canvas.Pixels[ii+1,jj]=clGreen) then

begin

Form4.PaintBox1.Canvas.Pixels[ii+1,jj]:=clBlack;

Form4.Image1.Canvas.Pixels[ii+1,jj]:=clBlack;

end;

end;

for ii:=0 to 2*ZX do

for jj:=0 to ZY do begin

if (Form4.PaintBox1.Canvas.Pixels[ii,jj]=clGreen) or

(Form4.PaintBox1.Canvas.Pixels[ii,jj]=clRed) then

begin

Form4.PaintBox1.Canvas.Pixels[ii,jj]:=clWhite;

Form4.Image1.Canvas.Pixels[ii,jj]:=clWhite;

end;

end;

end;

Form4.PaintBox1.Canvas.Brush.Style:=bsClear;

Form4.PaintBox1.Canvas.Rectangle(Round(xw[4]),Round(yw[4]),

Round(xw[2]+1),Round(yw[2]+1));

Form4.Image1.Canvas.Brush.Style:=bsClear;

Form4.Image1.Canvas.Rectangle(Round(xw[4]),Round(yw[4]),

Round(xw[2]+1),Round(yw[2]+1));

end;

procedure TForm6.Button2Click(Sender: TObject);

begin

Close;

end;

end.

Za pomocą programu 4.7 wykonano wykresy warstwicowe czterech następujących funkcji:

1)

(4.148)

2)

(4.149)

3)

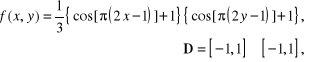
(4.150)

Rys. 4.23

Rys. 4.24

4)

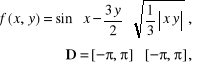
(4.151)

przyjmując we wszystkich przypadkach: Wykresy kolejnych funkcji (4.148) ÷ (4.151) zostały przedstawione na rysunkach 4.23 ÷ 4.26.

Rys. 4.25

Rys. 4.26

*

Interpolacyjną funkcję sklejaną wyznaczymy w podobny sposób jak dwuliniową funkcję sklejaną (4.147), po uprzednim zapisaniu funkcji sklejanej (4.70) w postaci

(4.152)

gdzie:

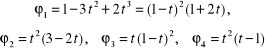
i obliczeniu w przybliżony sposób pochodnych , i we wszystkich węzłach siatki Δ .

Uogólniając wzór (4.152) wyznaczamy najpierw i na wszystkich liniach y = const

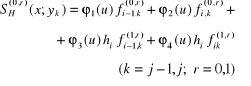
(4.153)

i następnie w wyniku ponownej interpolacji funkcji i mamy

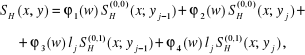
(4.154)

gdzie i określone są zależnościami (4.144) i (4.146).

Wprowadzając wektory:

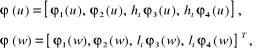
(4.155)

możemy równania (4.153) i (4.154) zapisać w postaciach:

i następnie po ich połączeniu uzyskujemy dogodny do obliczeń zapis macierzowy:

(4.156)

gdzie

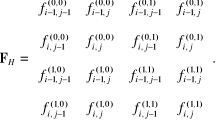
Dla interpolacyjnej wielomianowej funkcji sklejanej
(z defektem jeden względem obu zmiennych) z równania (4.108) najpierw obliczamy

(4.157)

gdzie

i w drugim etapie, analogicznie do (4.154), otrzymujemy

(4.158)

Występujące we wzorach (4.157) i (4.158) pochodne wyznaczamy przy wykorzystaniu wielomianowej funkcji sklejanej trzeciego stopnia jednej zmiennej:

-
   dla  

-
   dla  

-
   dla   za pomocą funkcji sklejanej interpolującej w węzłach wartości

Po wprowadzeniu wektorów:

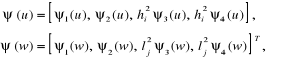
(4.159)

gdzie:

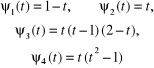
funkcję (4.158) możemy zapisać w postaci analogicznej do (4.156)

(4.160)

gdzie:

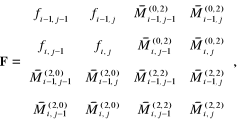
{Program 4.8a}

unit Obliczenia;

interface

uses

Windows, Messages, SysUtils, Classes, Graphics, Controls,

Forms, Dialogs, StdCtrls, Buttons;

type

Tabl = array[0..100] of Real;

. . . . . . . . . . . . . . . .

var

Form3: TForm3;

a,b,bl,dx1,dx2,dy1,dy2,delta,

eps,sm,u,w,xmin,xmax,ymin,ymax,x,y,z: Real;

derx,dery,derxy,zws: array[0..100,0..100] of Real;

i,ii,j,jj,K,kk,L,ll,licz,n,m: Integer;

fiu,fiw,fid: array[1..4] of Real;

maf: array[1..4,1..4] of Real;

der,xwez,ywez: Tabl;

plik,plik1: Text;

implementation

uses Ustawienia, Informacje, Grafika, Podglad;

{$R *.DFM}

function fun(x,y: Real): Real;

begin

if Form3.RadioButton1.Checked then

fun:=2*Exp(-2*(x*x+y*y));

if Form3.RadioButton2.Checked then

fun:=Sin(2*Sqrt(x*x+y*y));

if Form3.RadioButton3.Checked then

fun:=(Cos(Pi*(2*x-1))+1)*(Cos(Pi*(2*y-1))+1)/3;

if Form3.RadioButton4.Checked then

fun:=Sin(x-3*y/2)*Sqrt(Abs(x*y)/3);

end;

{procedure Pochodne1(n: Integer; xw,yw: Tabl; var der1: Tabl);}

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

procedure TForm3.BitBtn1Click(Sender: TObject);

label omin1,omin2;

begin

Form2.Show;

AssignFile(plik,Edit12.Text);

AssignFile(plik1,Edit11.Text);

Rewrite(plik); Rewrite(plik1);

Writeln(plik,'PROGRAM 4.8a.');

Writeln(plik,'Interpolacja funkcji dwóch zmiennych.');

Writeln(plik,'Dwusześcienna funkcja sklejana Hermite''a.');

n:=StrToInt(Edit1.Text); m:=StrToInt(Edit2.Text);

K:=StrToInt(Edit3.Text); L:=StrToInt(Edit4.Text);

xmin:=StrToFloat(Edit5.Text); xmax:=StrToFloat(Edit6.Text);

ymin:=StrToFloat(Edit7.Text); ymax:=StrToFloat(Edit8.Text);

delta:=StrToFloat(Edit9.Text); eps:=StrToFloat(Edit10.Text);

dx1:=(xmax-xmin)/n; dy1:=(ymax-ymin)/m;

Writeln(plik,'Rozmiary siatki węzłów:');

Writeln(plik,' - n = ',n:3); Writeln(plik,' - m = ',m:3);

Writeln(plik,'Liczby linii kraty:');

Writeln(plik,' - K = ',K:3); Writeln(plik,' - L = ',L:3);

Writeln(plik,'Kąt rzutowania - delta = ',delta:3);

Writeln(plik,'Kąt rzutowania - epsilon = ',eps:3);

Writeln(plik,'Rozmiary rozważanego obszaru prostokątnego:');

Writeln(plik,' - xmin = ',xmin:13);

Writeln(plik,' - xmax = ',xmax:13);

Writeln(plik,' - ymin = ',ymin:13);

Writeln(plik,' - ymax = ',ymax:13);

Writeln(plik1,K:3,' ',L:3);

Writeln(plik1,delta:3,' ',eps:3);

Writeln(plik1,xmin:13,' ',xmax:13,' ',ymin:13,' ',ymax:13);

Writeln(plik);

Writeln(plik,' i j z[i,j] błąd');

for i:=0 to n do begin

x:=xmin+i*dx1;

for j:=0 to m do begin

y:=ymin+j*dy1;

zws[i,j]:=fun(x,y);

end;

end;

for j:=0 to m do begin

for i:=0 to n do begin

xwez[i]:=xmin+i*dx1;

ywez[i]:=zws[i,j];

end;

Pochodne1(n,xwez,ywez,der);

for i:=0 to n do

derx[i,j]:=der[i];

end;

for i:=0 to n do begin

for j:=0 to m do begin

xwez[j]:=ymin+j*dy1;

ywez[j]:=zws[i,j];

end;

Pochodne1(m,xwez,ywez,der);

for j:=0 to M do

dery[i,j]:=der[j];

end;

for i:=0 to n do begin

for j:=0 to m do begin

xwez[j]:=ymin+j*dy1;

ywez[j]:=derx[i,j];

end;

Pochodne1(m,xwez,ywez,der);

for j:=0 to m do

derxy[i,j]:=der[j];

end;

licz:=0; bl:=0;

dx2:=(xmax-xmin)/K;

dy2:=(ymax-ymin)/L;

for kk:=0 to K do begin

x:=xmin+kk*dx2;

for ii:=1 to n do begin

a:=xmin+(ii-1)*dx1; b:=xmin+ii*dx1;

a:=x-a; b:=b-x; i:=ii;

if (a>=0) and (b>=0) then goto omin1;

end;

omin1:

for ll:=0 to L do begin

y:=ymin+ll*dy2;

for jj:=1 to m do begin

a:=ymin+(jj-1)*dy1; b:=ymin+jj*dy1;

a:=y-a; b:=b-y; j:=jj;

if (a>=0) and (b>=0) then goto omin2;

end;

omin2:

a:=xmin+(i-1)*dx1;

b:=ymin+(j-1)*dy1;

u:=(x-a)/dx1; w:=(y-b)/dy1;

fiu[1]:=(1-u)*(1-u)*(1+2*u);

fiu[2]:=u*u*(3-2*u);

fiu[3]:=dx1*u*(1-u)*(1-u);

fiu[4]:=dx1*u*u*(u-1);

fiw[1]:=(1-w)*(1-w)*(1+2*w);

fiw[2]:=w*w*(3-2*w);

fiw[3]:=dy1*w*(1-w)*(1-w);

fiw[4]:=dy1*w*w*(w-1);

maf[1,1]:=zws[i-1,j-1];

maf[1,2]:=zws[i-1,j];

maf[2,1]:=zws[i,j-1];

maf[2,2]:=zws[i,j];

maf[1,3]:=dery[i-1,j-1];

maf[1,4]:=dery[i-1,j];

maf[2,3]:=dery[i,j-1];

maf[2,4]:=dery[i,j];

maf[3,1]:=derx[i-1,j-1];

maf[3,2]:=derx[i-1,j];

maf[4,1]:=derx[i,j-1];

maf[4,2]:=derx[i,j];

maf[3,3]:=derxy[i-1,j-1];

maf[3,4]:=derxy[i-1,j];

maf[4,3]:=derxy[i,j-1];

maf[4,4]:=derxy[i,j];

for ii:=1 to 4 do begin

sm:=0;

for jj:=1 to 4 do

sm:=sm+maf[ii,jj]*fiw[jj];

fid[ii]:=sm;

end;

z:=0;

for ii:=1 to 4 do

z:=z+fiu[ii]*fid[ii];

licz:=licz+1;

if licz=5 then begin

licz:=0; Writeln(plik1);

end;

Write(plik1,z:13,' '); sm:=Abs(z-fun(x,y));

Writeln(plik,kk:3,' ',ll:3,' ',z:18,' ',sm:13);

if sm>bl then bl:=sm;

end;

end;

Writeln(plik);

Writeln(plik,'Norma błędu = ',bl:13);

CloseFile(plik); CloseFile(plik1);

Form2.Wyniki.Lines.LoadFromFile(Edit12.Text);

end;

. . . . . . . . . . . . . . . . . . . . . . .

procedure TForm3.BitBtn3Click(Sender: TObject);

begin

Close;

end;

end.

{Program 4.8b}

unit Obliczenia;

interface

uses

Windows, Messages, SysUtils, Classes, Graphics, Controls,

Forms, Dialogs, StdCtrls, Buttons;

type

Tabl = array[0..100] of Real;

. . . . . . . . . . . . . . . .

var

Form3: TForm3;

a,b,bl,dx1,dx2,dy1,dy2,delta,eps,

sm,u,w,xmin,xmax,ymin,ymax,x,y,z: Real;

derx,dery,derxy,zws: array[0..100,0..100] of Real;

i,ii,j,jj,K,kk,L,ll,licz,n,m: Integer;

fiu,fiw,fid: array[1..4] of Real;

maf: array[1..4,1..4] of Real;

der,xwez,ywez: Tabl;

plik,plik1: Text;

implementation

uses Ustawienia, Informacje, Grafika, Podglad;

{$R *.DFM}

{function fun(x,y: Real): Real;}

{procedure Pochodne2(n: Integer; xw,yw: Tabl; var der2: Tabl;

utw0,utwn: Integer; al0,aln,der0,dern,la0,

min,d0,dn: Real);}

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

procedure TForm3.BitBtn1Click(Sender: TObject);

label omin1,omin2;

begin

Form2.Show;

AssignFile(plik,Edit12.Text);

AssignFile(plik1,Edit11.Text);

Rewrite(plik); Rewrite(plik1);

Writeln(plik,'PROGRAM 4.8b.');

Writeln(plik,'Interpolacja funkcji dwóch zmiennych.');

Writeln(plik,'Bikubiczna funkcja sklejana z defektem 1.');

Writeln(plik);

n:=StrToInt(Edit1.Text); m:=StrToInt(Edit2.Text);

K:=StrToInt(Edit3.Text); L:=StrToInt(Edit4.Text);

xmin:=StrToFloat(Edit5.Text); xmax:=StrToFloat(Edit6.Text);

ymin:=StrToFloat(Edit7.Text); ymax:=StrToFloat(Edit8.Text);

delta:=StrToFloat(Edit9.Text); eps:=StrToFloat(Edit10.Text);

dx1:=(xmax-xmin)/n; dy1:=(ymax-ymin)/m;

Writeln(plik,'Rozmiary siatki węzłów:');

Writeln(plik,' - n = ',n:3); Writeln(plik,' - m = ',m:3);

Writeln(plik,'Liczby linii kraty:');

Writeln(plik,' - K = ',K:3); Writeln(plik,' - L = ',L:3);

Writeln(plik,'Kąt rzutowania - delta = ',delta:3);

Writeln(plik,'Kąt rzutowania - epsilon = ',eps:3);

Writeln(plik,'Rozmiary rozważanego obszaru prostokątnego:');

Writeln(plik,' - xmin = ',xmin:13);

Writeln(plik,' - xmax = ',xmax:13);

Writeln(plik,' - ymin = ',ymin:13);

Writeln(plik,' - ymax = ',ymax:13);

Writeln(plik1,K:3,' ',L:3);

Writeln(plik1,delta:3,' ',eps:3);

Writeln(plik1,xmin:13,' ',xmax:13,' ',ymin:13,' ',ymax:13);

Writeln(plik);

Writeln(plik,' i j z[i,j] błąd');

for i:=0 to n do begin

x:=xmin+i*dx1;

for j:=0 to m do begin

y:=ymin+j*dy1;

zws[i,j]:=fun(x,y);

end;

end;

for j:=0 to m do begin

for i:=0 to n do begin

xwez[i]:=xmin+i*dx1;

ywez[i]:=zws[i,j];

end;

Pochodne2(n,xwez,ywez,der,0,0,0,0,0,0,0,0,0,0);

for i:=0 to n do

derx[i,j]:=der[i];

end;

for i:=0 to n do begin

for j:=0 to m do begin

xwez[j]:=ymin+j*dy1;

ywez[j]:=zws[i,j];

end;

Pochodne2(m,xwez,ywez,der,0,0,0,0,0,0,0,0,0,0);

for j:=0 to m do

dery[i,j]:=der[j];

end;

for i:=0 to n do begin

for j:=0 to m do begin

xwez[j]:=ymin+j*dy1;

ywez[j]:=derx[i,j];

end;

Pochodne2(m,xwez,ywez,der,0,0,0,0,0,0,0,0,0,0);

for j:=0 to m do

derxy[i,j]:=der[j];

end;

licz:=0; bl:=0;

dx2:=(xmax-xmin)/K;

dy2:=(ymax-ymin)/L;

for kk:=0 to K do begin

x:=xmin+kk*dx2;

for ii:=1 to n do begin

a:=xmin+(ii-1)*dx1; b:=xmin+ii*dx1;

a:=x-a; b:=b-x; i:=ii;

if (a>=0) and (b>=0) then goto omin1;

end;

omin1:

for ll:=0 to L do begin

y:=ymin+ll*dy2;

for jj:=1 to m do begin

a:=ymin+(jj-1)*dy1; b:=ymin+jj*dy1;

a:=y-a; b:=b-y; j:=jj;

if (a>=0) and (b>=0) then goto omin2;

end;

omin2:

a:=xmin+(i-1)*dx1; b:=ymin+(j-1)*dy1;

u:=(x-a)/dx1; w:=(y-b)/dy1;

fiu[1]:=(1-u); fiu[2]:=u;

fiu[3]:=dx1*dx1*u*(u-1)*(2-u);

fiu[4]:=dx1*dx1*u*(u*u-1);

fiw[1]:=(1-w); fiw[2]:=w;

fiw[3]:=dy1*dy1*w*(w-1)*(2-w);

fiw[4]:=dy1*dy1*w*(w*w-1);

maf[1,1]:=zws[i-1,j-1];

maf[1,2]:=zws[i-1,j];

maf[2,1]:=zws[i,j-1];

maf[2,2]:=zws[i,j];

maf[1,3]:=dery[i-1,j-1]/6;

maf[1,4]:=dery[i-1,j]/6;

maf[2,3]:=dery[i,j-1]/6;

maf[2,4]:=dery[i,j]/6;

maf[3,1]:=derx[i-1,j-1]/6;

maf[3,2]:=derx[i-1,j]/6;

maf[4,1]:=derx[i,j-1]/6;

maf[4,2]:=derx[i,j]/6;

maf[3,3]:=derxy[i-1,j-1]/36;

maf[3,4]:=derxy[i-1,j]/36;

maf[4,3]:=derxy[i,j-1]/36;

maf[4,4]:=derxy[i,j]/36;

for ii:=1 to 4 do begin

sm:=0;

for jj:=1 to 4 do

sm:=sm+maf[ii,jj]*fiw[jj];

fid[ii]:=sm;

end;

z:=0;

for ii:=1 to 4 do

z:=z+fiu[ii]*fid[ii];

licz:=licz+1;

if licz=5 then begin

licz:=0; Writeln(plik1);

end;

Write(plik1,z:13,' '); sm:=Abs(z-fun(x,y));

Writeln(plik,kk:3,' ',ll:3,' ',z:18,' ',sm:13 );

if sm>bl then bl:=sm;

end;

end;

Writeln(plik);

Writeln(plik,'Norma błędu = ',bl:13);

CloseFile(plik); CloseFile(plik1);

Form2.Wyniki.Lines.LoadFromFile(Edit12.Text);

end;

. . . . . . . . . . . . . . . . . . . . . . .

procedure TForm3.BitBtn3Click(Sender: TObject);

begin

Close;

end;

end.

Rys. 4.27

Interpolacja funkcji dwóch zmiennych
na siatce (4.138) dwusześcienną funkcją sklejaną Hermite'a (4.156) lub dwusześcienną funkcją sklejaną z defektem 1 (4.160) odbywa się w programach, odpowiednio, 4.8a i 4.8b. W programach tych z formularza Dane (rys. 4.27) wczytywane są dane sterujące przebiem obliczeń: rozmiary siatki (4.138), rozmiary interpolowanej kraty, liczby definiujące rozmiary rozważanego obszaru prostokątnego oraz kąty rzutowania ukośnego.

Obliczone za pomocą programów 4.8a i 4.8b wartości interpolowanych funkcji (4.148) ÷ (4.151) dla
oraz są wczytywane w module Rysunek, przeznaczonym do wizualizacji powierzchni funkcyjnych według algorytmu zamieszczonego w podręczniku [15]. W ten sposób uzyskano obrazy zamieszczone na rysunkach 4.28 ÷ 4.31.

Dodatkowo interpolowano funkcję (4.151) dla
(rys. 4.32) oraz
(rys. 4.33), aby pokazać wpływ przyjęcia zbyt małej liczby węzłów na prawidłowe odtworzenie przebiegu funkcji. Maksymalne błędy interpolacji były mniejsze w większości przypadków dla interpolacji funkcją sklejaną
za wyjątkiem funkcji (4.149), dla której interpolacja dwusześcienną funkcją sklejaną Hermite'a okazała się nieco dokładniejsza

Rys. 4.28

Rys. 4.29

Rys. 4.30

Rys. 4.31

Rys. 4.32

Rys. 4.33

254 4. Interpolacja

4.11. Interpolacja funkcji dwóch zmiennych 237

---