równanie (4.65) możemy przekształcić do postaci

(4.67)

określającej hiperboliczne funkcje sklejane (nazywane w literaturze anglojęzycznej „splines in tension”).

Zarówno wielomianowe funkcje sklejane, jak i hiperboliczne funkcje sklejane są przykładami algebraicznych funkcji sklejanych. W ostatnich latach rozwijany jest również drugi kierunek badań, w którym przez funkcje sklejane rozumie się takie elementy przestrzeni Sobolewa, które minimalizują określone funkcjonały - wynikające z ekstremalnych własności funkcji sklejanych, a szczególnie z własności minimalnej normy. Najczęściej są jednak wykorzystywane wielomianowe funkcje sklejane do stopnia trzeciego włącznie, ze względu na łatwość wyznaczania parametrów tych funkcji i możliwość uzyskiwania rozwiązań o wystarczającej w praktyce gładkości. Mogą one być stosowane do rozwiązywania różnych zagadnień numerycznych - począwszy od interpolacji, a skończywszy na przybliżonym rozwiązywaniu zagadnień opisywanych równaniami różniczkowymi cząstkowymi i całkowymi.

4.8. Wielomianowe funkcje sklejane trzeciego stopnia

Przedstawimy najpierw funkcję sklejaną Hermite'a (z defektem dwa), która charakteryzuje się następującymi własnościami:

- w każdym podprzedziale jest wielomianem trzeciego stopnia,

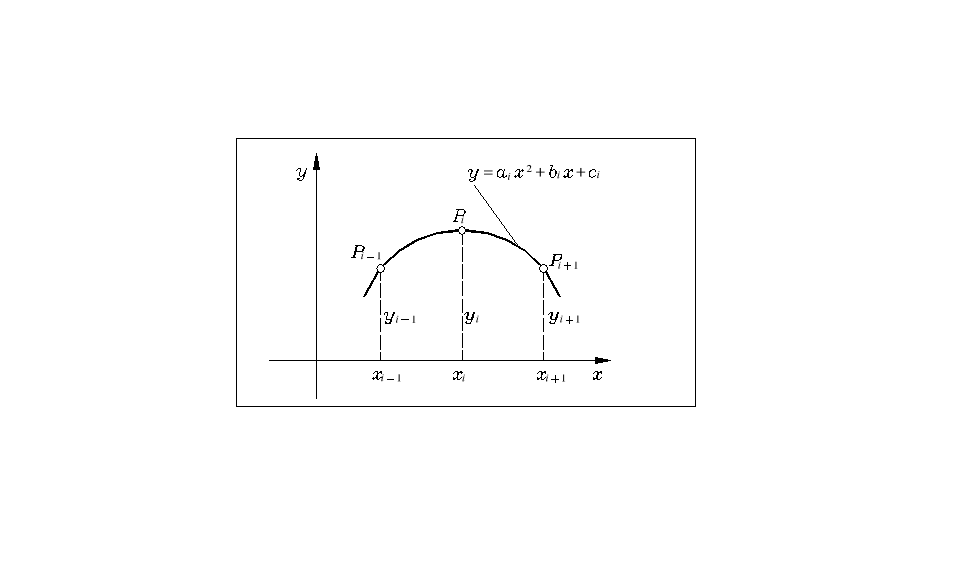
Rys. 4.16

- jest klasy ; co oznacza, że zarówno , jak i jej pochodna są funkcjami ciągłymi,

- spełnia warunki interpolacji, czyli ,

- przybiera we wszystkich węzłach interpolacji zadane wartości pierwszych pochodnych, tzn.

Niezbędne wartości pierwszych pochodnych we wszystkich węzłach , obliczymy przyjmując, że są one równe odpowiednim pochodnym wielomianów drugiego stopnia, przechodzących przez trzy kolejne punkty: (rys. 4.16); wyrażają się one poprzez następujące ilorazy różnicowe:

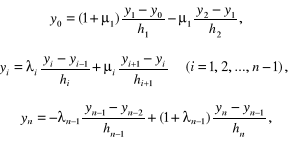
(4.68)

gdzie:

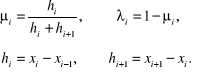
(4.69)

Ilorazy różnicowe (4.68) - (4.69) są drugiego rzędu dokładności, o czym łatwo można się przekonać po podstawieniu do nich rozwinięć i w szeregi Taylora względem punktu

Dla zadanych we wszystkich węzłach wartości i wielomianowa funkcja sklejana Hermite'a trzeciego stopnia jest w każdym podprzedziale określona wzorem

(4.70)

gdzie:

*

Wyprowadzenie równań wielomianowej funkcji sklejanej trzeciego stopnia, która należy do
(z defektem jeden) opiera się na zależności (4.58)

(4.71)

po wprowadzeniu oznaczenia

(4.72)

Całkując dwukrotnie obie części równania (4.71) uzyskujemy:

(4.73)

(4.74)

gdzie i
są stałymi. Stałe całkowania wyznaczamy z warunków interpolacji

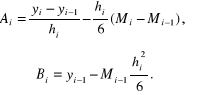
(4.75)

Pełne zdefiniowanie funkcji sklejanej wymaga jeszcze określenia wielkości W tym celu z równań (4.73) i (4.75a) obliczamy granice jednostronne:

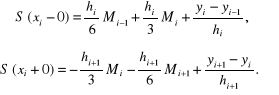
(4.76)

Ciągłość
i wynika z równań (4.71) oraz z równań (4.74) ÷ (4.75). Żądając natomiast ciągłości
w punktach

(4.77)

otrzymamy następujący układ równań

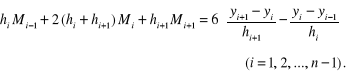
(4.78)

Równań (4.78) mamy
, natomiast liczba niewiadomych: wy-nosi
. Do tego układu należy dołączyć więc dwa dodatkowe równania. Dla okresowej funkcji sklejanej

(4.79)

równania te wynikają z warunków okresowości:

(4.80)

a dla nieokresowej funkcji sklejanej dołączamy dwa równania z następujących warunków brzegowych:

1) zadane pierwsze pochodne oraz Z równań (4.76) mamy:

(4.81)

2) zadane drugie pochodne:

(4.82)

3) ciągłość trzecich pochodnych w węzłach i oraz

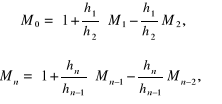
(4.83)

4) uogólnienie warunków pierwszego i drugiego rodzaju:

(4.84)

w których przyjmuje się zwykle oraz

Przy wykorzystaniu oznaczeń (4.69) układ równań (4.78) można zapisać w postaci:

(4.85)

i następnie, po uwzględnieniu dodatkowych równań wynikających z warunków brzegowych (4.76) ÷ (4.84), otrzymujemy następujące równanie macierzowe:

(4.86)

W równaniu (4.86) przez
oznaczono prawe strony równań (4.85), a
są modyfikacjami współczynników , wynikającymi z uwz-ględnienia warunków brzegowych. Przykładowo, dla warunków (4.83) i dla brzegu wstawiając zależności: do równania

po przekształceniach uzyskujemy:

(4.87)

Podobnie można zapisać w postaci macierzowej równania okresowej funkcji sklejanej:

(4.88)

przy czym na mocy (4.80) jest:

*

W zastosowaniach praktycznych potrzebna jest jeszcze często zależność typu (4.78) wiążąca wartości pierwszych pochodnych funkcji sklejanej z zadanymi wartościami funkcji. Czasami jest też wygodniej używać równań z pierwszymi pochodnymi, zamiast z drugimi.

Wprowadzamy, analogicznie do (4.72), oznaczenie

(4.89)

Z równań (4.76) mamy:

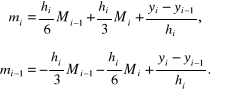
(4.90)

Po rozwiązaniu układu równań (4.90) względem wielkości oraz i wsta-wieniu ich do (4.73) ÷ (4.75) otrzymamy:

(4.91)

(4.92)

Różniczkując (4.92) dostajemy

(4.93)

oraz

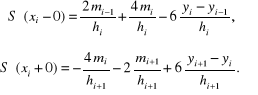
(4.94)

Spełnienie warunków ciągłości drugiej pochodnej wielomianowej funkcji sklejanej w punktach wymaga rozwiązania układu równań

(4.95)

który - po wykorzystaniu oznaczeń (4.69) - można zapisać następująco

(4.96)

Powyższe układy równań musimy, jak poprzednio, uzupełnić dwoma dodatkowymi równaniami. Dla okresowej funkcji sklejanej równania te wynikają z warunków okresowości.

Dla nieokresowej funkcji sklejanej stosujemy warunki (4.81) - (4.84) zapisane z użyciem pochodnych Kolejno mamy:

1) zadane pierwsze pochodne:

(4.97)

2) zadane drugie pochodne:

(4.98)

3) ciągłość trzecich pochodnych w węzłach

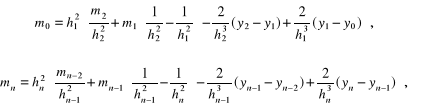
(4.99)

4) uogólnienie warunków (4.97) i (4.98):

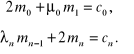
(4.100)

Układ (4.96) można zapisać również w postaci macierzowej, analogicznej do (4.86) i (4.88).

*

Często w obliczeniach numerycznych stosujemy podział równomierny wtedy układy równań (4.78) i (4.95) przyjmują prostsze postacie:

(4.101)

(4.102)

W niektórych zastosowaniach praktycznych wygodniej jest też korzystać z rów-nań (4.74) ÷ (4.75) oraz (4.91) przedstawionych w innych, równoważnych postaciach np. przekształcone równania (4.74) - (4.75) można zapisać następująco:

(4.103)

gdzie:

*

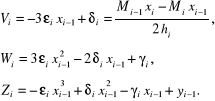
W przypadku zarówno układu równań (4.88), jak i układów równań (4.86) i (4.96) przy prawidłowo dobranych warunkach dodatkowych (4.81) ÷ (4.84) lub (4.97) ÷ (4.100) macierze współczynników są macierzami silnie diagonalnie dominującymi, gdyż moduły elementów leżących na głównych przekątnych są większe od sumy modułów pozostałych elementów leżących w tym samym wierszu. Stąd wynika wniosek, że te układy równań mają jednoznaczne rozwiązanie, co oznacza tym samym, że istnieje dokładnie jedna interpolacyjna wielomianowa funkcja sklejana trzeciego stopnia
.

Proste wyrażenia zezwalające na ocenę błędu interpolacji otrzymamy przy założeniu podziału równomiernego. Szukamy rozwiązania układu (4.101) przyjmując, że wielkości mogą być przedstawione w postaci:

(4.104)

Po podstawieniu (4.104) do (4.101) i rozwinięciu obu stron równania w szeregi Taylora:

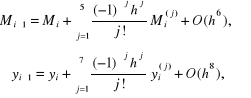
(4.105)

uzyskamy, po przyrównaniu współczynników przy pochodnych tego samego rzędu, następujące oszacowanie

(4.106)

W podobny sposób z (4.102) mamy

(4.107)

Wielomianowa funkcja sklejana trzeciego stopnia
może być w przedziale zapisana w postaci [20]

(4.108)

gdzie

Wykorzystując oszacowanie (4.106) i rozwinięcia: oraz i  w szeregi Taylora względem punktu otrzymujemy

(4.109)

gdzie

Po zróżniczkowaniu (4.109) uzyskamy oszacowania błędów aproksymacji pochodnych:

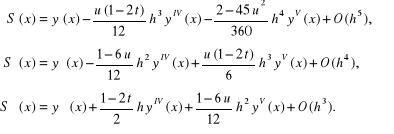
(4.110)

*

Obecnie przedstawiamy program komputerowy przeznaczony do wyznaczania omówionych wielomianowych funkcji sklejanych trzeciego stopnia, działający podobnie jak programy 4.1 ÷ 4.4.

{Program 4.5}

uses

Crt,Graph;

type

Tabl1=array[0..100] of Real;

Tabl2=array[1..1000] of Real;

var

fun,i,j,K,n,m,st,tr,utw0,utwn,X0,Y0,ZX,ZY: Integer;

a,b,bl,h,x,y,y1,y2: Real;

xx,yy,Xekr,Yekr: Tabl2;

der1,der2,xw,yw: Tabl1;

plik: Text;

zn: Char;

label powt;

function f(x: Real): Real;

begin

f:=1/(1+25*x*x);

end;

procedure Pochodne1(n: Integer; xw,yw: Tabl1; var der1: Tabl1);

var

i: Integer;

dy1,dy2,h1,h2,mi,la: Real;

begin

for i:=1 to n-1 do begin

h1:=xw[i]-xw[i-1];

h2:=xw[i+1]-xw[i];

dy1:=yw[i]-yw[i-1];

dy2:=yw[i+1]-yw[i];

mi:=h1/(h1+h2);

la:=1-mi;

der1[i]:=la*dy1/h1+mi*dy2/h2;

if i=1 then der1[0]:=(1+mi)*dy1/h1-mi*dy2/h2;

if i=n-1 then der1[n]:=-la*dy1/h1+(1+la)*dy2/h2;

end;

end;

procedure FunSklej1(n: Integer; x: Real; var y: Real;

xw,yw,der1: Tabl1);

var

i,j: Integer;

A,B,dy,h,t: Real;

label omin;

begin

for j:=1 to n do begin

i:=j; A:=x-xw[i-1]; B:=xw[i]-x;

if (A>=0) and (B>=0) then goto omin;

end;

omin:

h:=xw[i]-xw[i-1];

t:=(x-xw[i-1])/h;

dy:=yw[i]-yw[i-1];

A:=-2*dy/h+(der1[i-1]+der1[i]);

B:=-A+dy/h-der1[i-1];

y:=yw[i-1]+(x-xw[i-1])*(der1[i-1]+t*(B+t*A));

end;

procedure Pochodne2(n: Integer; xw,yw: Tabl1; var der2: Tabl1;

utw0,utwn: Integer; al0,aln,der0,dern,la0,

min,d0,dn: Real);

var

i,n1: Integer;

a0,an,dx1,dx2,dy1,dy2,h,p: Real;

a,c,d,q,u: Tabl1;

begin

n1:=n-1;

for i:=1 to n1 do begin

dx1:=xw[i+1]-xw[i];

dx2:=xw[i]-xw[i-1];

dy1:=yw[i+1]-yw[i];

dy2:=yw[i]-yw[i-1];

p:=xw[i+1]-xw[i-1];

c[i]:=dx1/p;

a[i]:=1-c[i];

d[i]:=6*(dy1/dx1-dy2/dx2)/p;

end;

if utw0=0 then begin

dx1:=(xw[1]-xw[0])/(xw[2]-xw[1]);

p:=1+a[1]*(1+dx1)/2;

c[1]:=(c[1]-a[1]*dx1)/p;

d[1]:=d[1]/p;

end;

if utwn=0 then begin

dx2:=(xw[n]-xw[n1])/(xw[n1]-xw[n-2]);

p:=1+c[n1]*(1+dx2)/2;

a[n1]:=(a[n1]-c[n1]*dx2)/p;

d[n1]:=d[n1]/p;

end;

if utw0=1 then begin

a0:=al0*Pi/180;

a0:=Cos(a0)/Sin(a0);

h:=1/(xw[1]-xw[0]);

p:=1/(1-0.25*a[1]);

dx1:=3*h*((yw[1]-yw[0])*h-a0);

c[1]:=c[1]*p;

d[1]:=(d[1]-a[1]*dx1)*p;

end;

if utwn=1 then begin

an:=aln*Pi/180;

an:=Cos(an)/Sin(an);

h:=1/(xw[n]-xw[n1]);

p:=1/(1-0.25*c[n1]);

dx2:=3*h*(an-(yw[n]-yw[n1])*h);

a[n1]:=a[n1]*p;

d[n1]:=(d[n1]-c[n1]*dx2)*p;

end;

if utw0=2 then d[1]:=d[1]-a[1]*der0;

if utwn=2 then d[n1]:=d[n1]-c[n1]*dern;

if utw0=3 then begin

p:=1/(1-0.25*a[1]*la0);

dy1:=a[1]*d0/2;

c[1]:=c[1]*p;

d[1]:=(d[1]-dy1)*p;

end;

if utwn=3 then begin

p:=1/(1-0.25*c[n1]*min);

dy2:=c[n1]*dn/2;

a[n1]:=a[n1]*p;

d[n1]:=(d[n1]-dy2)*p;

end;

q[1]:=-0.5*c[1];

u[1]:= 0.5*d[1];

for i:=2 to n1 do begin

p:=1/(2+a[i]*q[i-1]);

q[i]:=-c[i]*p;

u[i]:=(d[i]-a[i]*u[i-1])*p;

end;

der2[n1]:=u[n1];

for i:=n1-1 downto 1 do

der2[i]:=der2[i+1]*q[i]+u[i];

if utw0=0 then der2[0]:=(1+dx1)*der2[1]-dx1*der2[2];

if utwn=0 then der2[n]:=(1+dx2)*der2[n1]-dx2*der2[n-2];

if utw0=1 then der2[0]:=dx1-0.5*der2[1];

if utwn=1 then der2[n]:=dx2-0.5*der2[n1];

if utw0=2 then der2[0]:=der0;

if utwn=2 then der2[n]:=dern;

if utw0=3 then der2[0]:=d0/2-la0*der2[1]/2;

if utwn=3 then der2[n]:=dn/2-min*der2[n1]/2;

end;

Procedure FunSklej2(n:Integer; x:Real; var y,y1,y2: Real;

xw,yw,der2: Tabl1);

var

i,j: Integer;

A,B,h,h1,h2: Real;

label omin;

begin

for j:=1 to n do begin

i:=j; h1:=x-xw[i-1]; h2:=xw[i]-x;

if (h1>=0) and (h2>=0) then goto omin;

end;

omin:

h:=xw[i]-xw[i-1];

y2:=(der2[i]*h1+der2[i-1]*h2)/h;

A:=(yw[i]-yw[i-1])/h-h*(der2[i]-der2[i-1])/6;

B:=yw[i-1]-h*h*der2[i-1]/6;

y1:=0.5*(der2[i]*h1*h1-der2[i-1]*h2*h2)/h+A;

y:=(der2[i]*h1*h1*h1+der2[i-1]*h2*h2*h2)/h/6+A*h1+B;

end;

{procedure Normalizacja(K,A,B: Integer; xx,yy: Tabl2;

var Xekr,Yekr: Tabl2);}

{procedure Osie(X0,Y0,A,B: Integer; x,y: String);}

begin

powt:

ClrScr;

Writeln('PROGRAM 4.5. Dane do obliczen:');

Write(' - funkcja sklejana(1/2): fun = '); Read(fun);

Write(' - poczatek przedzialu: a = '); Readln(a);

Write(' - koniec przedzialu: b = '); Readln(b);

Write(' - liczba wezlow: n = '); Readln(n);

Write(' - liczba punktow wykresu: m = '); Readln(m);

Assign(plik,'Pr_4_5.wyn');

Rewrite(plik);

Writeln(plik,'PROGRAM 4.5');

Writeln(plik,'Interpolacja funkcji jednej zmiennej.');

case fun of

1: Writeln(plik,'Funkcja sklejana Hermite''a trzeciego
stopnia.');

2: Writeln(plik,'Funkcja sklejana trzeciego stopnia.');

end;

Writeln(plik);

Writeln(plik,'Poczatek przedzialu: a = ',a:13);

Writeln(plik,'Koniec przedzialu: b = ',b:13);

Writeln(plik,'Liczba wezlow: n = ',n:3);

Writeln(plik,'Liczba punktow wykresu: m = ',m:3);

Writeln(plik);

h:=(b-a)/n;

for i:=0 to n do begin

x:=a+i*h;

y:=f(x);

xw[i]:=x;

yw[i]:=y;

xx[i+1]:=x;

yy[i+1]:=y;

end;

xx[n+2]:=0; yy[n+2]:=0;

K:=n+2; st:=Detect;

InitGraph(st,tr,'c:\tp\bgi');

if GraphResult < 0 then Halt(1);

ZX:=GetMaxX; ZY:=GetMaxY;

Writeln(plik,'Wyniki interpolacji funkcji:');

Writeln(plik,' i x[i] y[i] blad');

case fun of

1: Pochodne1(n,xw,yw,der1);

2: Pochodne2(n,xw,yw,der2,0,0,0,0,0,0,0,0,0,0);

end;

h:=(b-a)/m;

for i:=0 to m do begin

x:=a+i*h;

case fun of

1: FunSklej1(n,x,y,xw,yw,der1);

2: FunSklej2(n,x,y,y1,y2,xw,yw,der2);

end;

bl:=f(x)-y;

Writeln(plik,i:3,' ',x:13,' ',y:13,' ',bl:13);

K:=K+1; xx[K]:=x; yy[K]:=y;

end;

Close(plik);

Normalizacja(K,ZX-50,ZY-50,xx,yy,Xekr,Yekr);

SetColor(Red);

X0:=Round(Xekr[n+2]+25);

Y0:=Round(Yekr[n+2]+25);

Osie(X0,Y0,ZX,ZY,'x','y');

SetViewPort(25,25,ZX-25,ZY-25,ClipOff);

SetColor(Yellow);

for i:=1 to n+1 do begin

X0:=Round(Xekr[i]);

Y0:=Round(Yekr[i]);

Circle(X0,Y0,2);

FloodFill(X0,Y0,Yellow);

end;

MoveTo(Round(Xekr[n+3]),Round(Yekr[n+3]));

for i:=n+4 to K do

LineTo(Round(Xekr[i]),Round(Yekr[i]));

SetColor(Green);

SetLineStyle(3,0,1);

SetViewPort(0,0,ZX,ZY,ClipOff);

Rectangle(ZX-200,0,ZX,17);

OutTextXY(ZX-190,5,'Nowe obliczenia: (t/n)?');

Repeat until KeyPressed;

RestoreCrtMode;

zn:=ReadKey;

if zn='t' then goto powt;

CloseGraph;

end.

W programie 4.5 wykorzystywane są cztery procedury o nazwach:

- Pochodne1(n,xw,yw,der1), przeznaczona do obliczania pochodnych (4.68),

- FunSklej1(n,x,y,xw,yw,der1), której zadaniem jest obliczanie wartości wielomianowej funkcji sklejanej (4.70),

- Pochodne2(n,xw,yw,der2,utw0,utwn,al0,aln,der0,dern,la0,min, d0,dn), w której rozwiązywany jest układ równań (4.86) przy wykorzystaniu algorytmu (2.78) - (2.79),

- FunSklej2(n,x,y,y1,y2,xw,yw,der2), obliczająca wartości wielomianowej funkcji sklejanej
oraz jej pochodnych ze wzorów (4.71) ÷ (4.75).

Znaczenie parametrów formalnych wszystkich procedur jest następujące:

n - liczba węzłów,

xw,yw[0..n] - tablice zawierające odcięte i rzędne punktów wyznaczających interpolowaną funkcję,

der1[0..n] - tablica zawierająca obliczane wartości pochodnych (4.68),

x,y - zmienne zawierające wartości zadanej odciętej
i obliczanych wartości funkcji sklejanych (4.70) lub (4.74) ÷ (4.75),

der2[0..n] - tablica zawierająca wartości drugich pochodnych (4.72) funkcji sklejanej
,

utw0,utwn - zmienne typu całkowitego określające rodzaj warunków brzegowych; dla zadanych wartości tych zmiennych wynoszących 0, 1, 2 lub 3 korzysta się, odpowiednio, z warunków (4.83), (4.81), (4.82) lub (4.84),

al0,aln - zadane kąty nachylenia stycznych (w stopniach dla x = a oraz x = b, jeśli korzystamy z warunków brzegowych (4.81),

der0,dern - zadane drugie pochodne dla x = a oraz x = b, jeśli korzystamy z warunków (4.82),

la0,min,d0,dn - zmienne te mają identyczne znaczenie ze znaczeniem parametrów występujących w warunkach (4.84),

y1,y2 - obliczane wartości pierwszej i drugiej pochodnej funkcji
.

W zależności od wyboru alternatywy obliczeń zbiór zadanych punktów
interpolowany jest albo za pomocą funkcji sklejanej ( Fun = 1), albo też za pomocą funkcji sklejanej
( Fun = 2).

Wyniki obliczeń dotyczące interpolowania funkcji (4.32) zawierają załączone tabulogramy komputerowe oraz są przedstawione na rysunku 4.17.

PROGRAM 4.5

Interpolacja funkcji jednej zmiennej.

Funkcja sklejana Hermite'a trzeciego stopnia.

Poczatek przedzialu: a = -1.000000E+00

Koniec przedzialu: b = 1.000000E+00

Liczba wezlow: n = 20

Liczba punktow wykresu: m = 100

Wyniki interpolacji funkcji:

i x[i] y[i] blad

0 -1.000000E+00 3.846154E-02 0.000000E+00

1 -9.800000E-01 3.992760E-02 5.640459E-05

2 -9.600000E-01 4.152036E-02 7.697578E-05

3 -9.400000E-01 4.323982E-02 6.897268E-05

4 -9.200000E-01 4.508597E-02 4.038094E-05

5 -9.000000E-01 4.705882E-02 0.000000E+00

6 -8.800000E-01 4.913091E-02 -1.500081E-05

7 -8.600000E-01 5.130225E-02 6.117895E-06

8 -8.400000E-01 5.361400E-02 3.406713E-05

9 -8.200000E-01 5.610737E-02 4.086345E-05

10 -8.000000E-01 5.882353E-02 0.000000E+00

11 -7.800000E-01 6.171454E-02 -2.422478E-05

12 -7.600000E-01 6.475294E-02 1.389820E-05

13 -7.400000E-01 6.801065E-02 6.286457E-05

14 -7.200000E-01 7.155960E-02 7.363738E-05

15 -7.000000E-01 7.547170E-02 0.000000E+00

16 -6.800000E-01 7.965859E-02 -4.075185E-05

17 -6.600000E-01 8.407232E-02 3.197120E-05

18 -6.400000E-01 8.884544E-02 1.225354E-04

19 -6.200000E-01 9.411048E-02 1.402243E-04

20 -6.000000E-01 1.000000E-01 0.000000E+00

21 -5.800000E-01 1.063422E-01 -7.229950E-05

22 -5.600000E-01 1.130488E-01 7.337559E-05

23 -5.400000E-01 1.203774E-01 2.499033E-04

24 -5.200000E-01 1.285856E-01 2.804231E-04

25 -5.000000E-01 1.379310E-01 0.000000E+00

26 -4.800000E-01 1.480700E-01 -1.410324E-04

27 -4.600000E-01 1.588308E-01 1.517427E-04

28 -4.400000E-01 1.707289E-01 5.039642E-04

29 -4.200000E-01 1.842801E-01 5.627774E-04

30 -4.000000E-01 2.000000E-01 0.000000E+00

31 -3.800000E-01 2.172647E-01 -3.449818E-04

32 -3.600000E-01 2.357305E-01 1.185526E-04

33 -3.400000E-01 2.563332E-01 7.362522E-04

34 -3.200000E-01 2.800085E-01 8.903883E-04

35 -3.000000E-01 3.076923E-01 0.000000E+00

36 -2.800000E-01 3.390154E-01 -1.177547E-03

37 -2.600000E-01 3.733538E-01 -1.606634E-03

38 -2.400000E-01 4.112615E-01 -1.425473E-03

39 -2.200000E-01 4.532923E-01 -8.036199E-04

40 -2.000000E-01 5.000000E-01 0.000000E+00

41 -1.800000E-01 5.547077E-01 -2.221504E-03

42 -1.600000E-01 6.170462E-01 -7.290056E-03

43 -1.400000E-01 6.820308E-01 -1.088983E-02

44 -1.200000E-01 7.446769E-01 -9.382805E-03

45 -1.000000E-01 8.000000E-01 0.000000E+00

46 -8.000000E-02 8.528000E-01 9.268966E-03

47 -6.000000E-02 9.064000E-01 1.103119E-02

48 -4.000000E-02 9.536000E-01 7.938462E-03

49 -2.000000E-02 9.872000E-01 2.899010E-03

50 0.000000E+00 1.000000E+00 0.000000E+00

51 2.000000E-02 9.872000E-01 2.899010E-03

52 4.000000E-02 9.536000E-01 7.938462E-03

53 6.000000E-02 9.064000E-01 1.103119E-02

54 8.000000E-02 8.528000E-01 9.268966E-03

55 1.000000E-01 8.000000E-01 0.000000E+00

56 1.200000E-01 7.446769E-01 -9.382805E-03

57 1.400000E-01 6.820308E-01 -1.088983E-02

58 1.600000E-01 6.170462E-01 -7.290056E-03

59 1.800000E-01 5.547077E-01 -2.221504E-03

60 2.000000E-01 5.000000E-01 0.000000E+00

61 2.200000E-01 4.532923E-01 -8.036199E-04

62 2.400000E-01 4.112615E-01 -1.425473E-03

63 2.600000E-01 3.733538E-01 -1.606634E-03

64 2.800000E-01 3.390154E-01 -1.177547E-03

65 3.000000E-01 3.076923E-01 0.000000E+00

66 3.200000E-01 2.800085E-01 8.903883E-04

67 3.400000E-01 2.563332E-01 7.362522E-04

68 3.600000E-01 2.357305E-01 1.185526E-04

69 3.800000E-01 2.172647E-01 -3.449818E-04

70 4.000000E-01 2.000000E-01 2.273737E-13

71 4.200000E-01 1.842801E-01 5.627774E-04

72 4.400000E-01 1.707289E-01 5.039642E-04

73 4.600000E-01 1.588308E-01 1.517427E-04

74 4.800000E-01 1.480700E-01 -1.410324E-04

75 5.000000E-01 1.379310E-01 0.000000E+00

76 5.200000E-01 1.285856E-01 2.804231E-04

77 5.400000E-01 1.203774E-01 2.499033E-04

78 5.600000E-01 1.130488E-01 7.337559E-05

79 5.800000E-01 1.063422E-01 -7.229950E-05

80 6.000000E-01 1.000000E-01 0.000000E+00

81 6.200000E-01 9.411048E-02 1.402243E-04

82 6.400000E-01 8.884544E-02 1.225354E-04

83 6.600000E-01 8.407232E-02 3.197120E-05

84 6.800000E-01 7.965859E-02 -4.075185E-05

85 7.000000E-01 7.547170E-02 0.000000E+00

86 7.200000E-01 7.155960E-02 7.363738E-05

87 7.400000E-01 6.801065E-02 6.286457E-05

88 7.600000E-01 6.475294E-02 1.389820E-05

89 7.800000E-01 6.171454E-02 -2.422478E-05

90 8.000000E-01 5.882353E-02 0.000000E+00

91 8.200000E-01 5.610737E-02 4.086345E-05

92 8.400000E-01 5.361400E-02 3.406713E-05

93 8.600000E-01 5.130225E-02 6.117895E-06

94 8.800000E-01 4.913091E-02 -1.500081E-05

95 9.000000E-01 4.705882E-02 0.000000E+00

96 9.200000E-01 4.508597E-02 4.038094E-05

97 9.400000E-01 4.323982E-02 6.897268E-05

98 9.600000E-01 4.152036E-02 7.697578E-05

99 9.800000E-01 3.992760E-02 5.640459E-05

100 1.000000E+00 3.846154E-02 0.000000E+00

PROGRAM 4.5

Interpolacja funkcji jednej zmiennej.

Funkcja sklejana trzeciego stopnia.

Poczatek przedzialu: a = -1.000000E+00

Koniec przedzialu: b = 1.000000E+00

Liczba wezlow: n = 20

Liczba punktow wykresu: m = 100

Wyniki interpolacji funkcji:

i x[i] y[i] blad

0 -1.000000E+00 3.846154E-02 0.000000E+00

1 -9.800000E-01 3.999938E-02 -1.537539E-05

2 -9.600000E-01 4.161607E-02 -1.873086E-05

3 -9.400000E-01 4.332356E-02 -1.477063E-05

4 -9.200000E-01 4.513383E-02 -7.472382E-06

5 -9.000000E-01 4.705882E-02 0.000000E+00

6 -8.800000E-01 4.911052E-02 5.395837E-06

7 -8.600000E-01 5.130087E-02 7.491191E-06

8 -8.400000E-01 5.364185E-02 6.218751E-06

9 -8.200000E-01 5.614541E-02 2.816743E-06

10 -8.000000E-01 5.882353E-02 0.000000E+00

11 -7.800000E-01 6.168992E-02 3.918949E-07

12 -7.600000E-01 6.476538E-02 1.456490E-06

13 -7.400000E-01 6.807246E-02 1.056137E-06

14 -7.200000E-01 7.163372E-02 -4.793953E-07

15 -7.000000E-01 7.547170E-02 0.000000E+00

16 -6.800000E-01 7.961214E-02 5.690076E-06

17 -6.600000E-01 8.409353E-02 1.075510E-05

18 -6.400000E-01 8.895753E-02 1.044032E-05

19 -6.200000E-01 9.424580E-02 4.908208E-06

20 -6.000000E-01 1.000000E-01 0.000000E+00

21 -5.800000E-01 1.062675E-01 2.424619E-06

22 -5.600000E-01 1.131185E-01 3.694858E-06

23 -5.400000E-01 1.206288E-01 -1.544375E-06

24 -5.200000E-01 1.288744E-01 -8.386603E-06

25 -5.000000E-01 1.379310E-01 0.000000E+00

26 -4.800000E-01 1.478904E-01 3.859845E-05

27 -4.600000E-01 1.589069E-01 7.565391E-05

28 -4.400000E-01 1.711505E-01 8.234034E-05

29 -4.200000E-01 1.847915E-01 5.133809E-05

30 -4.000000E-01 2.000000E-01 0.000000E+00

31 -3.800000E-01 2.169635E-01 -4.374974E-05

32 -3.600000E-01 2.359395E-01 -9.044540E-05

33 -3.400000E-01 2.572030E-01 -1.335919E-04

34 -3.200000E-01 2.810289E-01 -1.300718E-04

35 -3.000000E-01 3.076923E-01 0.000000E+00

36 -2.800000E-01 3.375225E-01 3.153477E-04

37 -2.600000E-01 3.710667E-01 6.805129E-04

38 -2.400000E-01 4.089266E-01 9.094798E-04

39 -2.200000E-01 4.517038E-01 7.848855E-04

40 -2.000000E-01 5.000000E-01 0.000000E+00

41 -1.800000E-01 5.540542E-01 -1.568055E-03

42 -1.600000E-01 6.126552E-01 -2.899143E-03

43 -1.400000E-01 6.742291E-01 -3.088178E-03

44 -1.200000E-01 7.372020E-01 -1.907879E-03

45 -1.000000E-01 8.000000E-01 -9.094947E-13

46 -8.000000E-02 8.605990E-01 1.469964E-03

47 -6.000000E-02 9.151739E-01 2.257316E-03

48 -4.000000E-02 9.594493E-01 2.089210E-03

49 -2.000000E-02 9.891498E-01 9.492595E-04

50 0.000000E+00 1.000000E+00 0.000000E+00

51 2.000000E-02 9.891498E-01 9.492595E-04

52 4.000000E-02 9.594493E-01 2.089210E-03

53 6.000000E-02 9.151739E-01 2.257316E-03

54 8.000000E-02 8.605990E-01 1.469964E-03

55 1.000000E-01 8.000000E-01 -9.094947E-13

56 1.200000E-01 7.372020E-01 -1.907879E-03

57 1.400000E-01 6.742291E-01 -3.088178E-03

58 1.600000E-01 6.126552E-01 -2.899143E-03

59 1.800000E-01 5.540542E-01 -1.568055E-03

60 2.000000E-01 5.000000E-01 -4.547474E-13

61 2.200000E-01 4.517038E-01 7.848855E-04

62 2.400000E-01 4.089266E-01 9.094798E-04

63 2.600000E-01 3.710667E-01 6.805129E-04

64 2.800000E-01 3.375225E-01 3.153477E-04

65 3.000000E-01 3.076923E-01 0.000000E+00

66 3.200000E-01 2.810289E-01 -1.300718E-04

67 3.400000E-01 2.572030E-01 -1.335919E-04

68 3.600000E-01 2.359395E-01 -9.044540E-05

69 3.800000E-01 2.169635E-01 -4.374974E-05

70 4.000000E-01 2.000000E-01 0.000000E+00

71 4.200000E-01 1.847915E-01 5.133809E-05

72 4.400000E-01 1.711505E-01 8.234034E-05

73 4.600000E-01 1.589069E-01 7.565391E-05

74 4.800000E-01 1.478904E-01 3.859845E-05

75 5.000000E-01 1.379310E-01 0.000000E+00

76 5.200000E-01 1.288744E-01 -8.386603E-06

77 5.400000E-01 1.206288E-01 -1.544375E-06

78 5.600000E-01 1.131185E-01 3.694857E-06

79 5.800000E-01 1.062675E-01 2.424619E-06

80 6.000000E-01 1.000000E-01 -2.273737E-13

81 6.200000E-01 9.424580E-02 4.908208E-06

82 6.400000E-01 8.895753E-02 1.044032E-05

83 6.600000E-01 8.409353E-02 1.075510E-05

84 6.800000E-01 7.961214E-02 5.690076E-06

85 7.000000E-01 7.547170E-02 0.000000E+00

86 7.200000E-01 7.163372E-02 -4.793952E-07

87 7.400000E-01 6.807246E-02 1.056137E-06

................................................

Rys. 4.17

214 4. Interpolacja

4.8. Wielomianowe funkcje sklejane trzeciego stopnia 205

---