6.2.3. Metoda kollokacji funkcjami sklejanymi

Rozważymy dwa algorytmy dotyczące najczęściej wykorzystywanego przypadku, gdy węzły kollokacji pokrywają się z węzłami funkcji sklejanej.

Określając dodatkowe węzły (4.113) dla równomiernej siatki (6.84) za pomocą stałego kroku siatki h:

rozwiązanie zagadnienia (6.82) - (6.83) aproksymować będziemy funkcją skle-janą trzeciego stopnia

Parametry funkcji sklejanej trzeciego stopnia wyznaczymy żądając, aby spełniała ona równanie różniczkowe (6.82) w każdym węźle kollokacji

(6.93)

i warunki brzegowe:

(6.94)

gdzie:

Zastępując w równaniu (6.93) wszystkie wielkości oraz zależnościami określonymi wzorami (4.122), wynikającymi z przedstawienia funkcji sklejanej za pomocą B-funkcji, otrzymamy algorytm niewiele różniący się od algorytmu metody różnic skończonych

gdyż jego realizacja polega również na rozwiązaniu układu równań liniowych z trój-diagonalną macierzą współczynników

(6.95)

gdzie:

W podobny sposób przy wykorzystaniu wzorów (4.122) zapisujemy warunki brzegowe:

i stąd obliczamy:

(6.96)

gdzie:

Wzory (6.96) pozwalają na pełne określenie układu równań (6.95), po modyfikacjach postaci jego początkowych i końcowych współczynników:

(6.97)

*

Na podstawie oszacowań (4.110) stwierdzamy, że przedstawiona metoda kol-lokacji funkcjami sklejanymi trzeciego stopnia jest, tak samo jak opisana w rozdziale poprzednim metoda różnic skończonych, metodą drugiego rzędu.

Znaczne zwiększenie dokładności aproksymacji równania (6.82) uzyskamy wykorzystując aproksymację drugiej pochodnej rzędu czwartego

(6.98)

otrzymaną po dodaniu stronami wyrażenia na klasyczną aproksymację drugiej pochodnej różnicami skończonymi - wzór (5.15)

do wyrażenia (4.106) na aproksymację drugiej pochodnej drugą pochodną funkcji sklejanej trzeciego stopnia

i wykorzystaniu równania (4.101).

Przy okazji zauważmy, że wyrażenie na aproksymację trzeciej pochodnej za pomocą pochodnych można wyznaczyć z trzeciego oszacowania (4.110). Mamy:

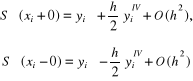
i następnie na mocy (4.71) i (4.122) jest

(6.99)

Aproksymację dla czwartej pochodnej łatwo można uzyskać po podstawieniu aproksymacji (6.98) dla do (4.106)

(6.100)

Po zastąpieniu w równaniu (6.82) pochodnych w wewnętrznych węzłach kollokacji wzorami (6.98) otrzymamy układ równań z pięciodiagonalną macierzą współczynników

(6.101)

gdzie:

Do zamknięcia układu równań (6.101) brakuje czterech równań. Okazuje się więc, że oprócz równań (6.96) - wynikających z warunków brzegowych, do układu (6.101) musimy jeszcze dołączyć takie dwa dodatkowe równania, które powinny zachowywać przyjętą dokładność aproksymacji równą

Analizując postać oszacowania (4.110b) stwierdzamy, że w dwóch punktach każ-dego podprzedziału o współrzędnych określonych parametrami

(6.102)

jest
Zatem przy wykorzystaniu oszacowań (4.110) możemy napisać dwa związki [20]:

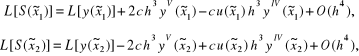
gdzie:

i następnie po ich dodaniu stronami dostajemy

gdzie:

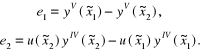
Biorąc pod uwagę fakt, że
otrzymujemy ostatecznie zależność

pozwalającą na uzyskanie dwóch brakujących równań. Są one następujące:

(6.103)

gdzie:

(6.104)

Po wyrażeniu funkcji sklejanej przez B-funkcje (4.121) równania (6.103) przybierają postać:

(6.105)

gdzie:

Z układów równań (6.96) i (6.105) wyznaczamy:

(6.106)

gdzie:

Uwzględnienie w układzie równań (6.101) zależności (6.106) powoduje modyfikacje następujących jego współczynników:

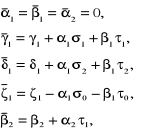
(6.107a)

(6.107a-cd.)

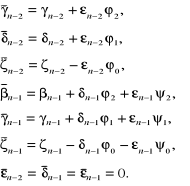
(6.107b)

Warto w tym miejscu jeszcze wspomnieć, że schematy różnicowe oparte na wykorzystaniu funkcji sklejanych są szczególnymi przypadkami niejawnych (kom-paktowych) schematów różnicowych postaci [32]

(6.108)

w których występują niejawne zależności różnicowe między wartościami funkcji w trzech kolejnych węzłach oraz jej pierwszymi i drugimi pochodnymi.

Różne postacie schematów (6.108) otrzymujemy z równań wynikających z warunków znikania określonych błędów aproksymacji, po rozwinięciu , oraz w szeregi Taylora wokół punktu np.:

*

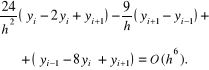
Metoda kollokacji funkcjami sklejanymi czwartego rzędu dokładności została wykorzystana w programie 6.7 do przybliżonego wyznaczania rozwiązania zagadnienia (6.90) - (6.91). Program 6.7 działa w taki sam sposób jak program 6.6. Wy-korzystano w nim, zaczerpniętą z programu 5.4, procedurę funkcyjną Bf(i,x, a,h) oraz dwie nowe procedury funkcyjne Bf1(i,x,a,h) i Bf2(i,x,a,h) - przeznaczone do obliczania pochodnych i B-funkcji sklejanej (4.117) - (4.118).

{Program 6.7}

unit Obliczenia;

interface

uses

Windows, Messages, SysUtils, Classes, Graphics, Controls,

Forms, Dialogs, StdCtrls, Buttons;

. . . . . . . . . . . . . . . . .

var

Form3: TForm3;

al,be,ga,de,ep,dz,y: array[0..250] of Real;

a,a0,a1,a2,b,b0,b1,b2,bl,dela,delb,

Fd,fi0,fi1,fi2,h,h1,h2,Hd,ks,p,Pd,

psi0,psi1,psi2,Qd,ui,vi,s,t1,t2,

sig0,sig1,sig2,tau0,tau1,tau2,x: Real;

q,qf,r,u: array[-1..250] of Real;

Cd,Dd: array[-1..1] of Real;

ksi: array[1..4] of Real;

Ed: array[-1..2] of Real;

Gd: array[-2..1] of Real;

i,j,n,n1,n2: Integer;

plik: Text;

implementation

uses Ustawienia, Informacje, Grafika, Podglad;

{$R *.DFM}

{function urr(x: Real): Real;}

{function vrr(x: Real): Real;}

{function wrr(x: Real): Real;}

{function yd(x: Real): Real;}

{function Bf(j,x,a,h: Real): Real;}

{function Bf1(j,x,a,h: Real): Real;}

{function Bf2(j,x,a,h: Real): Real;}

. . . . . . . . . . . . . . . . .

procedure TForm3.BitBtn1Click(Sender: TObject);

label powt;

begin

Form2.Show;

AssignFile(plik,Edit10.Text);

Rewrite(plik); Writeln(plik,'PROGRAM 6.7.');

Writeln(plik,'Zagadnienie brzegowe dla równania');

Writeln(plik,'różniczkowego zwyczajnego.');

Writeln(plik,'Metoda kollokacji funkcjami sklejanymi.');

Writeln(plik); a:=StrToFloat(Edit1.Text);

b:=StrToFloat(Edit2.Text); n:=StrToInt(Edit3.Text);

a0:=StrToFloat(Edit4.Text); a1:=StrToFloat(Edit5.Text);

a2:=StrToFloat(Edit6.Text); b0:=StrToFloat(Edit7.Text);

b1:=StrToFloat(Edit8.Text); b2:=StrToFloat(Edit9.Text);

Writeln(plik,'Liczba podprzedziałów: n = ',n:3);

Writeln(plik,'Początek przedziału: a = ',a:13);

Writeln(plik,'Koniec przedziału: b = ',b:13);

Writeln(plik,'Stałe określające warunki brzegowe:');

Writeln(plik,' - a1, a2, a0 = ',a1:9:6,a2:11:6,a0:11:6);

Writeln(plik,' - b1, b2, b0 = ',b1:9:6,b2:11:6,b0:11:6);

Writeln(plik); Writeln(plik,'Obliczone wartości funkcji:');

Writeln(plik,' i x[i] y[i] błąd');

n1:=n-1; n2:=n-2; h:=(b-a)/n; h1:=1/h; h2:=h1*h1/12;

for i:=1 to n1 do begin

x:=a+i*h; ui:=h1*urr(x)/2;

vi:=vrr(x)/6; al[i]:=h2;

be[i]:=8*h2-ui+vi;

ga[i]:=-18*h2+4*vi;

de[i]:=8*h2+ui+vi;

ep[i]:=h2; dz[i]:=wrr(x)

end;

dela:=a1*h-3*a2; Cd[-1]:=6*a0*h/dela;

Cd[0]:=-4*a1*h/dela; Cd[1]:=-(a1*h+3*a2)/dela;

delb:=b1*h+3*b2; Dd[1]:=6*b0*h/delb;

Dd[0]:=-4*b1*h/delb; Dd[-1]:=(3*b2-b1*h)/delb;

t1:=0.5-Sqrt(3)/6; t2:=0.5+Sqrt(3)/6;

ksi[1]:=a+t1*h; ksi[2]:=a+t2*h;

ksi[3]:=b-h+t1*h; ksi[4]:=b-h+t2*h;

for i:=-1 to 2 do begin

s:=0;

for j:=1 to 2 do begin

ks:=ksi[j];

s:=s+Bf2(i,ks,a,h);

s:=s+urr(ks)*Bf1(i,ks,a,h);

s:=s+vrr(ks)*Bf(i,ks,a,h);

end;

Ed[i]:=s;

end;

for i:=-2 to 1 do begin

s:=0;

for j:=3 to 4 do begin

ks:=ksi[j];

s:=s+Bf2(n+i,ks,a,h);

s:=s+urr(ks)*Bf1(n+i,ks,a,h);

s:=s+vrr(ks)*Bf(n+i,ks,a,h);

end;

Gd[i]:=s;

end;

Fd:=wrr(ksi[1])+wrr(ksi[2]);

Hd:=wrr(ksi[3])+wrr(ksi[4]);

Pd:=Ed[0]+Ed[-1]*Cd[0];

tau0:=(Fd-Ed[-1]*Cd[-1])/Pd;

tau1:=-(Ed[1]+Ed[-1]*Cd[1])/Pd;

tau2:=-Ed[2]/Pd; sig0:=Cd[-1]+Cd[0]*tau0;

sig1:=Cd[1]+Cd[0]*tau1;

sig2:=Cd[0]*tau2; Qd:=Gd[0]+Dd[0]*Gd[1];

fi0:=(Hd-Gd[1]*Dd[1])/Qd;

fi1:=-(Gd[-1]+Gd[1]*Dd[-1])/Qd;

fi2:=-Gd[-2]/Qd; psi0:=Dd[1]+Dd[0]*fi0;

psi1:=Dd[-1]+Dd[0]*fi1; psi2:=Dd[0]*fi2;

ga[1]:=ga[1]+al[1]*sig1+be[1]*tau1;

de[1]:=de[1]+al[1]*sig2+be[1]*tau2;

dz[1]:=dz[1]-al[1]*sig0-be[1]*tau0;

be[2]:=be[2]+al[2]*tau1;

ga[2]:=ga[2]+al[2]*tau2;

dz[2]:=dz[2]-al[2]*tau0;

al[1]:=0; be[1]:=0; al[2]:=0;

ga[n2]:=ga[n2]+ep[n2]*fi2;

de[n2]:=de[n2]+ep[n2]*fi1;

dz[n2]:=dz[n2]-ep[n2]*fi0;

be[n1]:=be[n1]+de[n1]*fi2+ep[n1]*psi2;

ga[n1]:=ga[n1]+de[n1]*fi1+ep[n1]*psi1;

dz[n1]:=dz[n1]-de[n1]*fi0-ep[n1]*psi0;

ep[n2]:=0; de[n1]:=0; ep[n1]:=0;

q[-1]:=0; r[-1]:=0; q[0]:=0;

r[0]:=0; u[-1]:=0; u[0]:=0;

for i:=1 to n1 do begin

p:=ga[i]+be[i]*q[i-1]+al[i]*r[i-2];

p:=p+al[i]*q[i-1]*q[i-2];;

q[i]:=-(de[i]+be[i]*r[i-1]+al[i]*q[i-2]*r[i-1])/p;

r[i]:=-ep[i]/p;

u[i]:=dz[i]-be[i]*u[i-1]-al[i]*u[i-2];

u[i]:=(u[i]-al[i]*q[i-2]*u[i-1])/p;

end;

qf[n1]:=u[n1];

qf[n2]:=q[n2]*qf[n1]+u[n2];

for i:=n-3 downto 1 do

qf[i]:=q[i]*qf[i+1]+r[i]*qf[i+2]+u[i];

qf[-1]:=sig0+sig1*qf[1]+sig2*qf[2];

qf[0]:=tau0+tau1*qf[1]+tau2*qf[2];

qf[n]:=fi0+fi1*qf[n1]+fi2*qf[n2];

qf[n+1]:=psi0+psi1*qf[n1]+psi2*qf[n2];

for i:=0 to n do

y[i]:=(qf[i-1]+4*qf[i]+qf[i+1])/6;

if (a2<>0) and (b2<>0) then

for i:=0 to n do

y[i]:=y[i]-y[0]+yd(a);

for i:=0 to n do begin

x:=a+i*h;

bl:=yd(x)-y[i];

Writeln(plik,i:3,' ',x:13,' ',y[i]:18,' ',bl:13);

end;

Writeln(plik); CloseFile(plik);

Form2.Wyniki.Lines.LoadFromFile(Edit10.Text);

end;

. . . . . . . . . . . . . . . . . . . . . . .

Wynikiem działania programu 6.7 są dwa kolejne wydruki, zawierające wyniki obliczeń dla dwóch zagadnień określonych równaniem (6.90) i warunkami brzegowymi (6.91) - wykorzystywanych uprzednio przy testowaniu poprawności działania programu 6.6. Porównanie tabulogramów wydruków otrzymanych za pomocą programów 6.6 i 6.7 potwierdza możliwość uzyskiwania bardzo dużej dokładności obliczeń przy zastosowaniu algorytmu opisanego wzorami (6.101) ÷ (1.107).

PROGRAM 6.7.

Zagadnienie brzegowe dla równania

różniczkowego zwyczajnego.

Metoda kollokacji funkcjami sklejanymi.

Liczba podprzedziałów: n = 40

Początek przedziału: a = -1.0000E+0000

Koniec przedziału: b = 1.0000E+0000

Stałe określające warunki brzegowe:

- a1, a2, a0 = 1.000000 0.000000 1.718282

- b1, b2, b0 = 1.000000 0.000000 3.718282

Obliczone wartości funkcji:

i x[i] y[i] błąd

0 -1.0000E+0000 1.718281828E+0000 5.6389E-0011

1 -9.5000E-0001 1.515760774E+0000 -9.6233E-0007

2 -9.0000E-0001 1.347909713E+0000 -1.7264E-0006

3 -8.5000E-0001 1.209577959E+0000 -2.2399E-0006

4 -8.0000E-0001 1.096483462E+0000 -2.5822E-0006

5 -7.5000E-0001 1.005057456E+0000 -2.7995E-0006

6 -7.0000E-0001 9.323191474E-0001 -2.9274E-0006

7 -6.5000E-0001 8.757742117E-0001 -2.9921E-0006

8 -6.0000E-0001 8.333324276E-0001 -3.0130E-0006

9 -5.5000E-0001 8.032406810E-0001 -3.0045E-0006

10 -5.0000E-0001 7.840283939E-0001 -2.9772E-0006

11 -4.5000E-0001 7.744630239E-0001 -2.9388E-0006

12 -4.0000E-0001 7.735137660E-0001 -2.8951E-0006

13 -3.5000E-0001 7.803219701E-0001 -2.8501E-0006

14 -3.0000E-0001 7.941770906E-0001 -2.8069E-0006

15 -2.5000E-0001 8.144972265E-0001 -2.7676E-0006

16 -2.0000E-0001 8.408135081E-0001 -2.7339E-0006

17 -1.5000E-0001 8.727577408E-0001 -2.7067E-0006

18 -1.0000E-0001 9.100528539E-0001 -2.6868E-0006

19 -5.0000E-0002 9.525058023E-0001 -2.6747E-0006

20 2.2737E-0013 1.000002671E+0000 -2.6706E-0006

21 5.0000E-0002 1.052505802E+0000 -2.6747E-0006

22 1.0000E-0001 1.110052854E+0000 -2.6868E-0006

23 1.5000E-0001 1.172757741E+0000 -2.7067E-0006

24 2.0000E-0001 1.240813508E+0000 -2.7338E-0006

25 2.5000E-0001 1.314497227E+0000 -2.7676E-0006

26 3.0000E-0001 1.394177091E+0000 -2.8068E-0006

27 3.5000E-0001 1.480321970E+0000 -2.8500E-0006

28 4.0000E-0001 1.573513766E+0000 -2.8950E-0006

29 4.5000E-0001 1.674463024E+0000 -2.9388E-0006

30 5.0000E-0001 1.784028394E+0000 -2.9772E-0006

31 5.5000E-0001 1.903240681E+0000 -3.0045E-0006

32 6.0000E-0001 2.033332428E+0000 -3.0130E-0006

33 6.5000E-0001 2.175774212E+0000 -2.9921E-0006

34 7.0000E-0001 2.332319147E+0000 -2.9274E-0006

35 7.5000E-0001 2.505057456E+0000 -2.7995E-0006

36 8.0000E-0001 2.696483461E+0000 -2.5822E-0006

37 8.5000E-0001 2.909577959E+0000 -2.2399E-0006

38 9.0000E-0001 3.147909713E+0000 -1.7263E-0006

39 9.5000E-0001 3.415760774E+0000 -9.6227E-0007

40 1.0000E+0000 3.718281828E+0000 5.8208E-0011

PROGRAM 6.7.

Zagadnienie brzegowe dla równania

różniczkowego zwyczajnego.

Metoda kollokacji funkcjami sklejanymi.

Liczba podprzedziałów: n = 40

Początek przedziału: a = -1.0000E+0000

Koniec przedziału: b = 1.0000E+0000

Stałe określające warunki brzegowe:

- a1, a2, a0 = 1.000000 0.000000 1.718282

- b1, b2, b0 = 1.000000 -1.000000 -2.718282

Obliczone wartości funkcji:

i x[i] y[i] błąd

0 -1.0000E+0000 1.718281828E+0000 5.8208E-0011

1 -9.5000E-0001 1.515761192E+0000 -1.3801E-0006

2 -9.0000E-0001 1.347910513E+0000 -2.5260E-0006

3 -8.5000E-0001 1.209579112E+0000 -3.3924E-0006

4 -8.0000E-0001 1.096484944E+0000 -4.0643E-0006

5 -7.5000E-0001 1.005059250E+0000 -4.5930E-0006

6 -7.0000E-0001 9.323212384E-0001 -5.0184E-0006

7 -6.5000E-0001 8.757765902E-0001 -5.3706E-0006

8 -6.0000E-0001 8.333350870E-0001 -5.6725E-0006

9 -5.5000E-0001 8.032436179E-0001 -5.9415E-0006

10 -5.0000E-0001 7.840316078E-0001 -6.1911E-0006

11 -4.5000E-0001 7.744665170E-0001 -6.4318E-0006

12 -4.0000E-0001 7.735175430E-0001 -6.6720E-0006

13 -3.5000E-0001 7.803260384E-0001 -6.9183E-0006

14 -3.0000E-0001 7.941814602E-0001 -7.1765E-0006

15 -2.5000E-0001 8.145019101E-0001 -7.4512E-0006

16 -2.0000E-0001 8.408185210E-0001 -7.7468E-0006

17 -1.5000E-0001 8.727631015E-0001 -8.0673E-0006

18 -1.0000E-0001 9.100585837E-0001 -8.4166E-0006

19 -5.0000E-0002 9.525119261E-0001 -8.7985E-0006

20 2.2737E-0013 1.000009217E+0000 -9.2171E-0006

. . . . . . . . . . . . . . . . . . . . . . . . . . .

31 5.5000E-0001 1.903255462E+0000 -1.7785E-0005

32 6.0000E-0001 2.033348534E+0000 -1.9120E-0005

33 6.5000E-0001 2.175791810E+0000 -2.0590E-0005

34 7.0000E-0001 2.332338428E+0000 -2.2208E-0005

35 7.5000E-0001 2.505078642E+0000 -2.3985E-0005

36 8.0000E-0001 2.696506810E+0000 -2.5930E-0005

37 8.5000E-0001 2.909603772E+0000 -2.8053E-0005

38 9.0000E-0001 3.147938345E+0000 -3.0358E-0005

39 9.5000E-0001 3.415792640E+0000 -3.2828E-0005

40 1.0000E+0000 3.718317418E+0000 -3.5590E-0005

402 6. Równania różniczkowe zwyczajne i całkowe

6.2. Zagadnienia brzegowe dla równań różniczkowych zwyczajnych 403

---