1 4 0.10 0.40 2.963212124E-0001 -2.4E-0003

1 5 0.10 0.50 3.115707208E-0001 -2.6E-0003

1 6 0.10 0.60 2.963214712E-0001 -2.4E-0003

1 7 0.10 0.70 2.520661637E-0001 -2.1E-0003

1 8 0.10 0.80 1.831368185E-0001 -1.5E-0003

1 9 0.10 0.90 9.628073415E-0002 -7.9E-0004

1 10 0.10 1.00 0.000000000E+0000 -1.7E-0020

2 0 0.20 0.00 0.000000000E+0000 0.0E+0000

2 1 0.20 0.10 1.831362877E-0001 -1.5E-0003

2 2 0.20 0.20 3.483462392E-0001 -2.9E-0003

2 3 0.20 0.30 4.794577779E-0001 -3.9E-0003

2 4 0.20 0.40 5.636367137E-0001 -4.6E-0003

2 5 0.20 0.50 5.926429336E-0001 -4.9E-0003

2 6 0.20 0.60 5.636370720E-0001 -4.6E-0003

2 7 0.20 0.70 4.794584185E-0001 -3.9E-0003

2 8 0.20 0.80 3.483469767E-0001 -2.9E-0003

2 9 0.20 0.90 1.831368648E-0001 -1.5E-0003

2 10 0.20 1.00 0.000000000E+0000 -3.2E-0020

3 0 0.30 0.00 0.000000000E+0000 0.0E+0000

3 1 0.30 0.10 2.520657055E-0001 -2.1E-0003

3 2 0.30 0.20 4.794577779E-0001 -3.9E-0003

3 3 0.30 0.30 6.599173494E-0001 -5.4E-0003

3 4 0.30 0.40 7.757796719E-0001 -6.4E-0003

3 5 0.30 0.50 8.157032372E-0001 -6.7E-0003

3 6 0.30 0.60 7.757800255E-0001 -6.4E-0003

3 7 0.30 0.70 6.599179961E-0001 -5.4E-0003

3 8 0.30 0.80 4.794585439E-0001 -3.9E-0003

3 9 0.30 0.90 2.520662943E-0001 -2.1E-0003

3 10 0.30 1.00 0.000000000E+0000 -4.4E-0020

4 0 0.40 0.00 0.000000000E+0000 0.0E+0000

4 1 0.40 0.10 2.963212124E-0001 -2.4E-0003

4 2 0.40 0.20 5.636367137E-0001 -4.6E-0003

4 3 0.40 0.30 7.757796719E-0001 -6.4E-0003

4 4 0.40 0.40 9.119839481E-0001 -7.5E-0003

4 5 0.40 0.50 9.589168502E-0001 -7.9E-0003

4 6 0.40 0.60 9.119842467E-0001 -7.5E-0003

4 7 0.40 0.70 7.757802238E-0001 -6.4E-0003

4 8 0.40 0.80 5.636373698E-0001 -4.6E-0003

4 9 0.40 0.90 2.963217195E-0001 -2.4E-0003

4 10 0.40 1.00 0.000000000E+0000 -5.2E-0020

5 0 0.50 0.00 0.000000000E+0000 0.0E+0000

5 1 0.50 0.10 3.115707208E-0001 -2.6E-0003

5 2 0.50 0.20 5.926429336E-0001 -4.9E-0003

5 3 0.50 0.30 8.157032372E-0001 -6.7E-0003

5 4 0.50 0.40 9.589168502E-0001 -7.9E-0003

5 5 0.50 0.50 1.008264986E+0000 -8.3E-0003

. . . . . . . . . . . . . . . . . . . . . . . . . . .

7.6. Siatkowe równania eliptyczne

Potrzeba rozwiązywania zagadnień brzegowych dla równania Poissona np. zagadnienia Dirichleta (7.91), bardzo często występuje w różnych zagadnieniach mechaniki, np. w numerycznej mechanice płynów przy wyznaczaniu ruchu płynów lepkich. Szybkość rozwiązywania układu równań (7.101) ma zasadniczy wpływ na efektywność algorytmów obliczeniowych wielu rozważanych zagadnień. Stąd też, oprócz najprostszych metod iteracyjnych przedstawionych w rozdziale poprzednim, do rozwiązywania algebraicznych układów równań z symetrycznymi macierzami współczynników stosowanych jest bardzo wiele różnych metod iteracyjnych [1, 11 - 12, 14, 32, 42 - 44]. Przedstawimy podstawowe idee algorytmów pięciu następujących metod:

- naprzemiennych kierunków,

- najszybszego spadku,

- sprzężonych gradientów,

- dwóch siatek,

- Stone'a.

O metodzie naprzemiennych kierunków wspominaliśmy już w rozdziale 7.3 (algorytm opisany wzorami (7.57) i (7.58)) przy omawianiu schematów różnicowych dla dwuwymiarowych równań parabolicznych.

Po zastąpieniu w równaniu (7.102) pochodnej względem czasu progresywną różnicą skończoną (5.4) oraz pochodnych względem zmiennych przestrzennych klasycznymi operatorami różnicowymi (5.15) drugiego rzędu dokładności otrzymamy zależność

(7.111)

gdzie:

Zależność (7.111) możemy przepisać w postaci

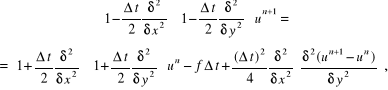
(7.112)

w której ostatni człon
na mocy oszacowania

może być pominięty.

Dokonując z kolei w zależności (7.112) podstawienia

uzyskujemy równanie

które można rozwiązać w dwóch etapach:

Etap I

(7.113a)

Etap II

(7.113b)

Otrzymaliśmy więc tym samym szereg równań z macierzami trójdiagonalnymi, które można rozwiązywać wyjątkowo prosto.

*

Dla macierzy symetrycznej i dodatnio określonej A , tzn. spełniającej nierówność można skonstruować metody iteracyjne wynikające z minimalizacji formy kwadratowej

(7.114)

osiągające jedyne minimum w rozwiązaniu układu Aby to sprawdzić wystarczy rozważyć różnicę

która na mocy definicji dodatniej określoności osiąga jedyne minimum dla

Metody prowadzące do minimalizacji formy (7.114) polegają na dobraniu wektora początkowego a następnie na dobraniu kierunku i odległości na tym kierunku, dających poprawiony wektor i ogólnie

(7.115)

W metodzie najszybszego spadku wektory wybieramy w kierunku najszybszej zmiany formy (7.114), tzn. w kierunku jej gradientu

(7.116)

gdzie:

Wynika stąd, że wektory są równe

(7.117)

Aby znaleźć współczynniki obliczamy

skąd dla

otrzymujemy

i ostatecznie uzyskujemy ciąg kolejnych przybliżeń

(7.118)

Zasadniczym pomysłem metody sprzężonych gradientów jest takie dobieranie kierunków, aby zagwarantować teoretycznie zbieżność po skończonej liczbie kroków.

Przyjmując wektory jako bazę n-wymiarowej przestrzeni euklidesowej, przy wykorzystaniu (7.115) możemy napisać

(7.119)

Oprócz tego w metodzie sprzężonych gradientów zakłada się, że wektory spełniają warunki A-ortogonalności

co pozwala na łatwe obliczanie współczynników

Ogólny algorytm metody sprzężonych gradientów wynika z procedury ortogonalizacji Grama-Schmidta [3]:

(7.120)

(7.120cd.)

W praktyce błędy zaokrągleń mogą zniekształcić teoretyczną zbieżność i uniemożliwić uzyskanie rozwiązania po n iteracjach. Użyteczną cechą metody sprzężonych gradientów jest jednak możliwość kontynuowania obliczeń aż do osiągnięcia dostatecznie małych residuów.

*

Przy stosowaniu większości metod iteracyjnych rozwiązywania algebraicznych układów równań liniowych można zaobserwować szybkie początkowe zmniejszanie się błędów określających kolejne wykonywane iteracje i następnie bardzo wolną ich zbieżność, pogarszającą się wraz ze zmniejszaniem się oczka siatki. Po rozłożeniu błędu rozwiązania iteracyjnego w szereg Fouriera można stwierdzić szybką początkową redukcję amplitudy modów o małej długości fal i bardzo wolne zmniejszanie się amplitudy modów o dużej długości fal. Spostrzeżenie to stało się podstawą rozwoju nowych metod iteracyjnych [43], nazywanych metodami wielu siatek (Multigrid Methods), w których obliczenia wykonywane są na siatkach o różnych rozmiarach oczek. Na każdej kolejnej siatce wykonywana jest zadana z góry niewielka liczba iteracji, niezbędna do zmniejszenia amplitudy składowych o wysokiej częstotliwości. Jest przy tym istotne, że składowe o niskiej częstotliwości na gęstej siatce stają się składowymi o wysokiej częstotliwości na siatce rzadkiej.

Istnieje wiele różnych odmian metody wielu siatek. W celu pokazania zasadniczej idei tych metod rozpatrzymy tylko bardzo prosty wariant obliczeń wykonywanych na dwóch siatkach z wykorzystaniem metody iteracji Gaussa-Seidela.

Zakładając, że znamy rozwiązanie przybliżone
na gęstej siatce o oczku h rozwiązywanie układu równań (7.101) metodą dwóch siatek będzie odbywało się w następujący sposób:

1) wykonanie
iteracji na gęstej siatce i obliczenie residuów

2) interpolacja residuów z siatki gęstej na siatkę rzadką o oczku

(7.121)

gdzie
jest operatorem interpolacji,

3) wykonanie
iteracji na rzadkiej siatce dla równania korekcyjnego, którego prawe strony są residuami - rozwiązanie

4) interpolacja rozwiązania korekcyjnego z siatki rzadkiej na siatkę gęstą

(7.122)

gdzie jest odwrotnym operatorem interpolacji do operatora (7.121),

5) korekta rozwiązania na siatce gęstej i wykonanie dodatkowych
iteracji - rozwiązanie

6) sprawdzenie warunku zakończenia obliczeń np.

(7.123)

Często w metodach wielu siatek układ równań na najrzadszej siatce jest rozwiązywany metodami dokładnymi.

*

Ostatnią z rozważanych metod jest metoda Stone'a [32, 41 - 42], nazywana również metodą SIP (Strongly Implicit Procedure). W metodzie tej macierz A układu równań (7.101)

(7.124)

w którym wektor niewiadomych oznaczono symbolem

zastępujemy różnicą dwóch macierzy

(7.125)

i tworzymy ciąg kolejnych przybliżeń

(7.126)

Zbieżność procesu iteracyjnego będzie tym szybsza im bardziej ściśle macierz C będzie aproksymować macierz A.

Rys. 7.11

Dla wyprowadzenia wzorów określających współczynniki macierzy C oraz D (7.125) zastosowany w układzie równań (7.124) operator różnicowy (7.96) przedstawimy w sposób symboliczny za pomocą kierunków stron świata (rys. 7.11a), a diagonale zawierające niezerowe elementy macierzy A oznaczymy symbolicznie w sposób pokazany na rysunku 7.11b.

Rys. 7.12

Macierz C w metodzie Stone'a rozkładana jest na iloczyn macierzy trójkątnej dolnej L i macierzy trójkątnej górnej U

(7.127)

jak to zostało symbolicznie przedstawione na rysunku 7.12. Po zapisaniu lewej strony układu równań (7.126) dla punktu P mamy

(7.128)

Następnie zakładamy

(7.129)

i równanie to zastępujemy równaniem następującym

(7.130)

w którym przyjmujemy:

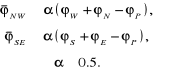
(7.131)

W ten sposób porównując równania (7.130) - (7.131) z równaniem (7.129) uzyskujemy wzory określające elementy macierzy D poprzez elementy macierzy C :

gdzie l oznacza numer kolumny w tych macierzach, a górny indeks N - liczbę oczek kwadratowej siatki

Korzystając z rysunku 7.12 obliczamy:

i następnie po podstawieniu otrzymanych zależności dla niezerowych elementów macierzy C i D do równania (7.127) uzyskujemy wzory określające kolejne elementy wektorów

Układ równań (7.126) zapisany w postaci

(7.132)

gdzie:

rozwiązujemy metodą Banachiewicza:

Etap I

(7.133)

Etap II

(7.134)

W programie 7.4, działającym w taki sam sposób jak program 7.3, do rozwiązania zagadnienia różnicowego (7.100) wykorzystano cztery pierwsze omawiane w tym rozdziale metody. W metodzie dwóch siatek rozwiązanie z siatki rzadkiej na siatkę gęstą interpolowano (7.122) za pomocą dwuliniowych funkcji sklejanych. Tabulogram modułu Obliczenia programu 7.4 jest następujący:

{Program 7.4}

unit Obliczenia;

interface

uses

Windows, Messages, SysUtils, Classes, Graphics, Controls,

Forms, Dialogs, StdCtrls, Buttons;

type

Tabl = array[0..100] of Real;

. . . . . . . . . . . . . . . . . . . . . . . . . . . . .

var

Form3: TForm3;

i,ii,iter,j,jj,k,l,licz,m1,m2,m3,n,nn,n1,n2,nr: Integer;

ar,u,un,urh,ur2h,r,rh,r2h: array[0..40,0..40] of Real;

bl,dt,eps,h,hh,h2,hh2,p,p1,p2,un1,x,y: Real;

aa,bb,cc,dd,up: Tabl;

plik: Text;

implementation

uses Ustawienia, Informacje, Grafika, Podglad;

{$R *.DFM}

function f(x,y: Real): Real;

begin

f:=-2*Pi*Pi*Sin(Pi*x)*Sin(Pi*y);

end;

function g(x,y: Real): Real;

begin

g:=0;

end;

function ud(x,y: Real): Real;

begin

ud:=Sin(Pi*x)*Sin(Pi*y);

end;

function akl(l,k,n1: Integer): Real;

begin

akl:=0; if k=l then akl:=4;

if (l=k+1) or (l=k-1) or (l=k+n1) or (l=k-n1) then akl:=-1;

if (l=k+1) and ((l-1) div n1 = (l-1)/n1) then akl:=0;

if (l=k-1) and (l div n1 = l/n1) then akl:=0;

end;

{procedure Tridiag1(n: Integer; a,b,c,d: Tabl;

var x: Tabl);}

procedure TForm3.BitBtn1Click(Sender: TObject);

label omin,omin1,omin2,powt1,powt2,powt3;

begin

Form2.Show;

AssignFile(plik,Edit5.Text);

Rewrite(plik);

Writeln(plik,'PROGRAM 7.4.');

Write(plik,'Zagadnienie Dirichleta');

Writeln(plik,' dla równania Poissona.');

n:=StrToInt(Edit1.Text);

iter:=StrToInt(Edit2.Text);

eps:=StrToFloat(Edit3.Text);

if RadioButton1.Checked then nr:=1;

if RadioButton2.Checked then nr:=2;

if RadioButton3.Checked then nr:=3;

if RadioButton4.Checked then nr:=4;

if nr=1 then begin

dt:=StrToFloat(Edit4.Text);

end;

if nr=4 then begin

m1:=StrToInt(Edit4.Text);

m2:=StrToInt(Edit6.Text);

m3:=StrToInt(Edit7.Text);

end;

case nr of

1: Writeln(plik,'Metoda naprzemiennych kierunków.');

2: Writeln(plik,'Metoda najszybszego spadku.');

3: Writeln(plik,'Metoda sprzężonych gradientów.');

4: Writeln(plik,'Metoda dwóch siatek.');

end;

Writeln(plik);

Writeln(plik,'Liczba podprzedziałów: N = ',n:4);

Writeln(plik,'Zadana liczba iteracji: iter = ',iter:4);

Writeln(plik,'Dokładność obliczeń: eps = ',eps:8);

if nr=1 then

Writeln(plik,'Krok czasowy: dt = ',dt:10);

if nr=4 then

Writeln(plik,'Liczby iteracji: m1, m2, m3 = ',

m1:3,',',m2:3,',',m3:3);

h:=1/N; h2:=h*h; n1:=n-1; nn:=n div 2;

n2:=nn-1; hh:=1/nn; hh2:=hh*hh;

for i:=0 to n do begin

un[i,0]:=0; u[i,0]:=0;

un[i,n]:=0; u[i,n]:=0;

end;

for j:=1 to n1 do begin

un[0,j]:=0; u[0,j]:=0;

un[n,j]:=0; u[n,j]:=0;

end;

for i:=1 to n1 do

for j:=1 to n1 do

un[i,j]:=g(i*h,j*h);

licz:=0; writeln(plik);

repeat

bl:=0; licz:=licz+1;

case nr of

1: begin

for i:=1 to n1 do begin

aa[i]:=-0.5*dt/h2;

bb[i]:=1+dt/h2;

cc[i]:=-0.5*dt/h2;

end;

aa[1]:=0; cc[n1]:=0;

for j:=1 to n1 do begin

for i:=1 to n1 do

dd[i]:=un[i,j]+0.5*dt*(un[i,j+1]-

2*un[i,j]+un[i,j-1])/h2-

dt*f(i*h,j*h);

Tridiag1(n1,aa,bb,cc,dd,up);

for i:=1 to n1 do u[i,j]:=up[i];

end;

for i:=1 to n1 do begin

for j:=1 to n1 do

dd[j]:=u[i,j]+0.5*dt*(u[i+1,j]-2*u[i,j]+

u[i-1,j])/h2;

Tridiag1(n1,aa,bb,cc,dd,up);

for j:=1 to n1 do begin

if Abs(up[j]-un[i,j])>bl then

bl:=Abs(up[j]-un[i,j]);

un[i,j]:=up[j];

end;

end;

for i:=1 to n1 do

for j:=1 to n1 do

u[i,j]:=un[i,j];

end;

2: begin

k:=0;

for j:=1 to n1 do

for i:=1 to n1 do begin

k:=k+1; p:=0; l:=0;

for jj:=1 to n1 do

for ii:=1 to n1 do begin

l:=l+1;

p:=p+akl(k,l,n1)*un[ii,jj];

end;

r[i,j]:=-h*h*f(i*h,j*h)-p;

end;

k:=0;

for j:=1 to n1 do

for i:=1 to n1 do begin

k:=k+1; p:=0; l:=0;

for jj:=1 to n1 do

for ii:=1 to n1 do begin

l:=l+1;

p:=p+akl(k,l,n1)*r[ii,jj];

end;

ar[i,j]:=p;

end;

p:=0;

for j:=1 to n1 do

for i:=1 to n1 do

p:=p+r[i,j]*r[i,j];

un1:=0;

for j:=1 to n1 do

for i:=1 to n1 do

un1:=un1+r[i,j]*ar[i,j];

un1:=p/un1; bl:=0;

for i:=1 to n1 do

for j:=1 to n1 do begin

u[i,j]:=un[i,j]+un1*r[i,j];

if Abs(u[i,j]-un[i,j])>bl then

bl:= Abs(u[i,j]-un[i,j]);

end;

end;

3: begin

if licz>1 then goto omin;

k:=0;

for j:=1 to n1 do

for i:=1 to n1 do begin

k:=k+1; p:=0; l:=0;

for jj:=1 to n1 do

for ii:=1 to n1 do begin

l:=l+1;

p:=p+akl(k,l,n1)*un[ii,jj];

end;

r[i,j]:=-h*h*f(i*h,j*h)-p;

ar[i,j]:=r[i,j];

end;

omin:

k:=0;

for j:=1 to n1 do

for i:=1 to n1 do begin

k:=k+1; p:=0; l:=0;

for jj:=1 to n1 do

for ii:=1 to n1 do begin

l:=l+1;

p:=p+akl(k,l,n1)*ar[ii,jj];

end;

u[i,j]:=p;

end;

p1:=0;

for j:=1 to n1 do

for i:=1 to n1 do

p1:=p1+ar[i,j]*r[i,j];

p2:=0;

for j:=1 to n1 do

for i:=1 to n1 do

p2:=p2+ar[i,j]*u[i,j];

un1:=p1/p2;

for i:=1 to n1 do

for j:=1 to n1 do

r[i,j]:=r[i,j]-un1*u[i,j];

bl:=0;

for i:=1 to n1 do

for j:=1 to n1 do begin

u[i,j]:=un[i,j]+un1*ar[i,j];

if Abs(u[i,j]-un[i,j])>bl then

bl:=Abs(u[i,j]-un[i,j]);

end;

k:=0;

for j:=1 to n1 do

for i:=1 to n1 do begin

k:=k+1; p:=0; l:=0;

for jj:=1 to n1 do

for ii:=1 to n1 do begin

l:=l+1;

p:=p+akl(k,l,N1)*r[ii,jj];

end;

un[i,j]:=p;

end;

p1:=0;

for j:=1 to n1 do

for i:=1 to n1 do

p1:=p1+ar[i,j]*un[i,j];

un1:=-p1/p2;

for i:=1 to n1 do

for j:=1 to n1 do

ar[i,j]:=r[i,j]+un1*ar[i,j];

end;

4: begin

for i:=1 to n1 do

for j:=1 to n1 do

u[i,j]:=un[i,j];

for i:=1 to n1 do

for j:=1 to n1 do begin

rh[i,j]:=0; r2h[i,j]:=0;

urh[i,j]:=0; ur2h[i,j]:=0;

end;

k:=0;

powt1: k:=k+1;

for i:=1 to n1 do

for j:=1 to n1 do begin

p:=u[i-1,j]+u[i+1,j];

p:=p+u[i,j-1]+u[i,j+1];

u[i,j]:=(p-h2*f(i*h,j*h))/4;

end;

if k<m1 then goto powt1;

for i:=1 to n1 do

for j:=1 to n1 do

rh[i,j]:=f(i*h,j*h)-(u[i-1,j]+u[i+1,j]+

u[i,j-1]+u[i,j+1]-4*u[i,j])/h2;

for i:=1 to n1 do

for j:=1 to n1 do begin

if (i div 2 = i/2) and

(j div 2 = j/2) then begin

ii:=i div 2; jj:=j div 2;

r2h[ii,jj]:=rh[i,j];

end;

end;

k:=0;

powt2: k:=k+1;

for i:=1 to n2 do

for j:=1 to n2 do begin

p:=ur2h[i-1,j]+ur2h[i+1,j];

p:=p+ur2h[i,j-1]+ur2h[i,j+1];

ur2h[i,j]:=(p-hh2*r2h[i,j])/4;

end;

if k<m2 then goto powt2;

for i:=1 to n1 do begin

x:=i*h;

for k:=0 to n2 do begin

ii:=k; p1:=2*h*k; p2:=2*h*(k+1);

if (x>=p1) and (x<=p2) then goto omin1;

end;

omin1:

for j:=1 to n1 do begin

y:=j*h;

for l:=0 to n2 do begin

jj:=l; p1:=2*h*l; p2:=2*h*(l+1);

if (y>=p1) and (y<=p2) then goto omin2;

end;

omin2:

p1:=0.5*(x-2*h*ii)/h;

p2:=0.5*(y-2*h*jj)/h;

p:=(1-p2)*((1-p1)*ur2h[ii,jj]+

p1*ur2h[ii+1,jj]);

urh[i,j]:=p+p2*((1-p1)*ur2h[ii,jj+1]+

p1*ur2h[ii+1,jj+1]);

end;

end;

for i:=1 to n1 do

for j:=1 to n1 do

u[i,j]:=u[i,j]+urh[i,j];

k:=0;

powt3: k:=k+1;

for i:=1 to n1 do

for j:=1 to n1 do begin

p:=u[i-1,j]+u[i+1,j];

p:=p+u[i,j-1]+u[i,j+1];

u[i,j]:=(p-h2*f(i*h,j*h))/4;

end;

if k<M3 then goto powt3;

for i:=1 to n1 do

for j:=1 to n1 do

if Abs(u[i,j]-un[i,j])>bl then

bl:=Abs(u[i,j]-un[i,j]);

end;

end; {case}

Writeln(plik,'iter = ',licz:3,' ','bl = ',bl:9);

for i:=1 to n1 do

for j:=1 to n1 do

un[i,j]:=u[i,j];

until (licz>=iter) or (bl<eps);

Writeln(plik);

Writeln(plik,'Liczba wykonanych iteracji: ',licz:3);

Writeln(plik);

Write(plik,'Wartości funkcji u(x[i],y[j])');

Writeln(plik,' dla i,j = 0,1,...,N:');

Write(plik,' i j x[i] y[j] u[i,j]');

Writeln(plik,' błąd');

for i:=0 to n do begin

x:=i*h;

for j:=0 to n do begin

y:=j*h; bl:=ud(x,y)-u[i,j];

Writeln(plik,i:3,' ',j:3,' ',x:5:2,' ',y:5:2,' ',

u[i,j]:18,' ',bl:9);

end;

end;

Writeln(plik); CloseFile(plik);

Form2.Wyniki.Lines.LoadFromFile(Edit5.Text);

end;

. . . . . . . . . . . . . . . . . . . . . .

498 7. Równania różniczkowe cząstkowe

7.6. Siatkowe równania eliptyczne 497

---