10 1.000000E+00 1.732042E+00 9.205900E-06

11 1.100000E+00 1.788831E+00 2.376880E-05

12 1.200000E+00 1.843893E+00 1.590741E-05

13 1.300000E+00 1.897336E+00 3.042294E-05

14 1.400000E+00 1.949334E+00 2.522146E-05

15 1.500000E+00 1.999960E+00 4.033430E-05

16 1.600000E+00 2.049352E+00 3.832083E-05

17 1.700000E+00 2.097563E+00 5.491633E-05

18 1.800000E+00 2.144704E+00 5.691913E-05

19 1.900000E+00 2.190814E+00 7.623076E-05

20 2.000000E+00 2.235984E+00 8.351309E-05

6.1.3. Metody Rungego-Kutty

Równanie (6.1) można scałkować między punktami i

(6.25)

i wykorzystać różnego rodzaju aproksymacje całki w prawej części tej zależności.

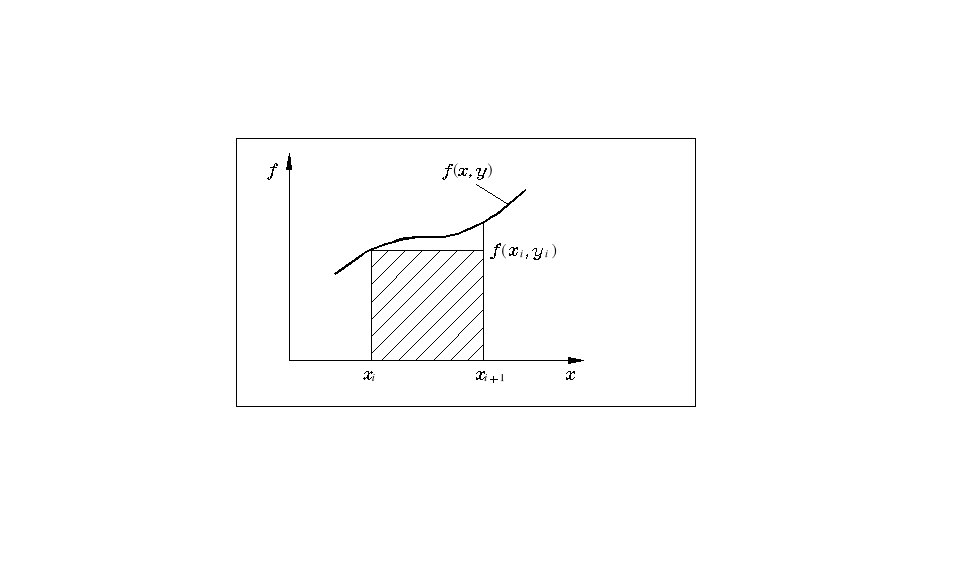
Rys. 6.1

Najprostszą aproksymacją całki w równaniu (6.25) jest przybliżenie funkcji podcałkowej
dla wszystkich x z przedziału
wartością funkcji
dla co jest równoważne przybliżeniu pola wyznaczonego przez wykres funkcji
prostokątem - rys. 6.1. W ten sposób otrzymujemy algorytm metody Eulera

(6.26)

gdzie

(6.27)

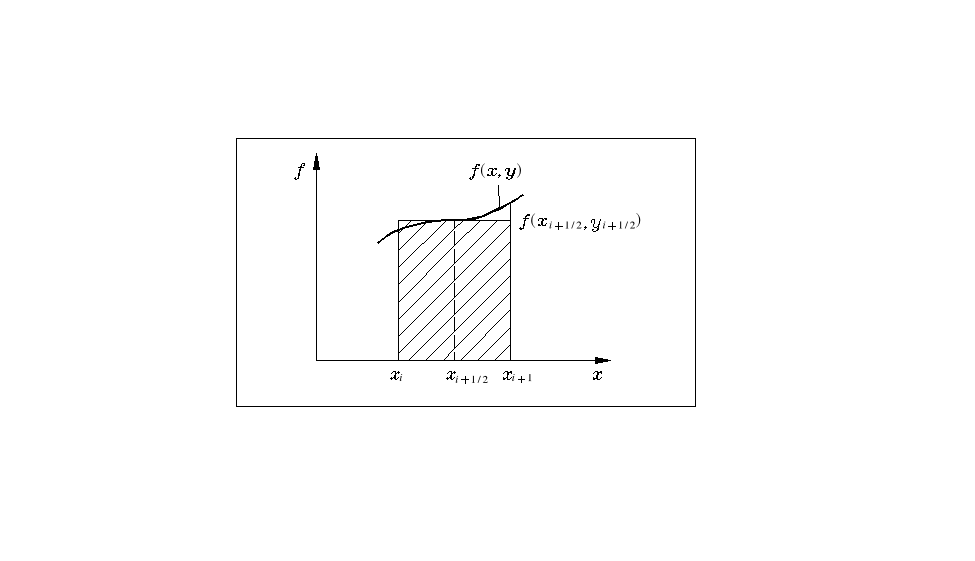
Rys. 6.2

Rozważmy teraz dwie proste koncepcje ulepszenia metody Eulera. Koncepcja pierwsza (rys. 6.2) opiera się na przybliżeniu pola pod krzywą
prostokątem o wysokości wyznaczonej w połowie przedziału
(kwadratura Gaussa z jednym węzłem)

(6.28)

Metoda (6.28) nazywana jest zmodyfikowaną metodą Eulera.

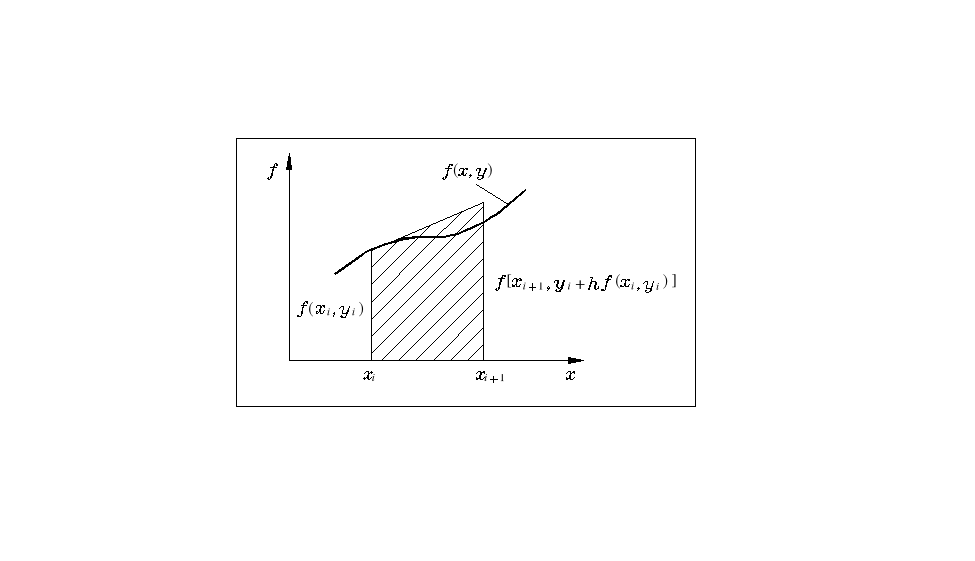
Rys. 6.3

Koncepcja druga wynika z zastępowania trapezów krzywoliniowych trapezami prostoliniowymi (rys. 6.3)

(6.29)

Tak ulepszona metoda Eulera nosi nazwę metody Heuna.

Uogólnieniem trzech omówionych metod jednokrokowych jest klasa metod Rungego-Kutty definiowanych wzorem

(6.30)

gdzie:

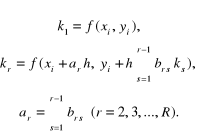
(6.31)

Liczbę całkowitą R nazywamy stopniem metody Rungego-Kutty.

W przypadku wzorów (6.26), (6.28) i (6.29) mamy:

- metoda Eulera

(6.32)

- zmodyfikowana metoda Eulera

R = 2, = 0, = 1, , (6.33)

- metoda Heuna

R = 2, , = 1. (6.34)

Naszym obecnym zadaniem jest określenie wielkości i z rozwinięć oraz funkcji w szeregi Taylora względem kroku h w otoczeniu punktu Niezbędne układy równań uzyskamy porównując współczynniki występujące przy jednakowych potęgach

Rozwinięcie jest następujące

. (6.35)

Kolejne pochodne ... obliczamy wielokrotnie różniczkując zależność (6.1):

i po ich wykorzystaniu otrzymujemy

(6.36)

W podobny sposób rozwijamy w szeregi potęgowe funkcje (r = 1, 2, ..., R )

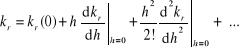
. (6.37)

Różniczkując funkcje:

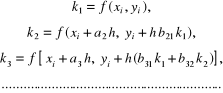
uzyskujemy:

i następnie mamy:

Powtórne różniczkowanie funkcji i daje następujące rezultaty [29, 30]:

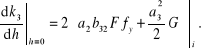
Po podstawieniu wszystkich przedstawionych rozwinięć do wzoru (6.30) otrzymujemy

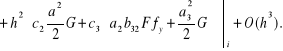
(6.38)

Stąd wynikają układy równań dla parametrów metod Rungego-Kutty stopnia pierwszego, drugiego i trzeciego:

(6.39)

(6.40)

W układzie równań (6.39) występują cztery niewiadome współczynniki; jeden z nich np. można potraktować jako parametr. Dwoma rozwiązaniami szczególny-mi, odpowiadającymi wartościom i = 1, są rozwiązania (6.33) i (6.34).

Układ sześciu równań (6.40) zawiera osiem niewiadomych, określa zatem dwuparametrową rodzinę współczynników. Obierając jako parametry współczynniki oraz można uzyskać dwie znane metody trzeciego stopnia [29, 30]:

- metoda Heuna

(6.41)

gdzie:

- metoda Kutty

(6.42)

gdzie:

Największe znaczenie praktyczne mają metody stopnia czwartego, dla których wyprowadzenie wzorów (6.31) jest dosyć żmudne i czasochłonne [1, 29]. Najbardziej popularnymi metodami stopnia czwartego są:

- metoda Rungego i Kutty

(6.43)

gdzie:

- metoda „trzech ósmych”

(6.44)

gdzie:

Wszystkie metody Rungego-Kutty dają się zapisać w postaci

(6.45)

w której znaną funkcję

(6.46)

nazywamy funkcją przyrostu.

Metoda (6.45) jest rzędu p, jeżeli p jest największą liczbą całkowitą, przy której

(6.47)

Na podstawie (6.30), (6.35) i (6.38) wnioskujemy, że osiągalny rząd metody Run-gego-Kutty jest równy jej stopniowi w rozważanych przez nas czterech przypadkach: R = 1, 2, 3, 4.

Porównując (6.1) z (6.45) stwierdzamy, że metoda jest zgodna, jeśli spełnia warunek

(6.48)

Dla każdej zgodnej metody Rungego-Kutty musi zatem być

(6.49)

Z (6.35) i (6.47) wynika, że warunek zgodności zapewnia jednocześnie zbieżność rozwiązania numerycznego do rozwiązania dokładnego Okazuje się ponadto, że dowolna zgodna metoda Rungego-Kutty jest co najmniej rzędu pierwszego.

Stabilność metod Rungego-Kutty w przypadku rozwiązań malejących można oprzeć na badaniu stabilności zagadnienia modelowego

(6.50)

gdzie jest liczbą rzeczywistą. Zbadamy mianowicie, jakie warunki musi spełniać długość kroku h, aby błąd występujący na kroku i nie wzrastał. Interesuje nas wzrost amplitudy błędu na kroku

(6.51)

gdzie g jest współczynnikiem wzmocnienia. Stabilność numeryczną osiągniemy przy spełnieniu warunku

(6.52)

Przykładowo dla metody stopnia pierwszego mamy

i następnie korzystając z wyjściowego równania (6.26) dostajemy równanie na przenoszenie małego błędu między kolejnymi krokami siatki

Stąd jest

(6.53)

gdzie

W podobny sposób przy wykorzystaniu związków (6.39) i (6.40) otrzymujemy:

(6.54)

(6.55)

Ważne w praktycznym stosowaniu metod Rungego-Kutty są przedziały stabilności absolutnej dla wynikające z warunku (6.52) [29, 30]

(6.56)

gdzie:

Omawianie metod Rungego-Kutty zakończymy uwagami o charakterze podsumowującym.

Metody Rungego-Kutty są metodami jednokrokowymi odznaczającymi się następującymi zaletami:

- są „samostartujące” tzn. nie wymagają żadnych dodatkowych wartości początkowych w celu wykonania pierwszego kroku obliczeń,

- formuły określające te metody są bardzo prostej postaci,

- dokonanie zmiany długości kroku całkowania nie wymaga żadnych dodatkowych zabiegów.

Wadami metod Rungego-Kutty są:

- duży koszt obliczeń prawych stron równania różniczkowego,

- trudności w oszacowaniu błędu obliczeń,

- mały obszar stabilności absolutnej sprawiający, że w przypadku równań źle uwarunkowanych metody te są całkowicie bezskuteczne.

Przedstawiamy obecnie program, którego zadaniem jest całkowanie zagadnienia (6.22) - (6.23) metodą Rungego-Kutty. Z klawiatury wczytywane są niezbędne dane do obliczeń objaśnione odpowiednimi tekstami ukazującymi się na ekranie monitora oraz nadawana jest wartość zmiennej rodz, typu całkowitego. Nadania wartości zmiennej rodz z zakresu 1 ÷ 7 oznacza wybór jednej z następujących metod Rungego-Kutty:

rodz = 1 - metoda Eulera (6.26),

rodz = 2 - zmodyfikowana metoda Eulera (6.28),

rodz = 3 - metoda Heuna drugiego rzędu (6.29),

rodz = 4 - metoda Heuna trzeciego rzędu (6.41),

rodz = 5 - metoda Kutty (6.42),

rodz = 6 - metoda Rungego-Kutty (6.43),

rodz = 7 - metoda „trzech ósmych” (6.44)

i jednocześnie automatyczne przypisanie wartości dla wszystkich współczynników metody. W przypadku nadania zmiennej rodz wartości większej od 7 wszystkie współczynniki określające wybraną metodę Rungego-Kutty są również wczytywane z klawiatury.

{Program 6.2}

uses

Crt;

var

i,j,n,R,rodz,s: Integer;

a,b,h,x,xx,y,ya,yn,yp,yy: Real;

ark: array[2..6] of Real;

crk,k: array[1..6] of Real;

brk: array[2..6,1..5] of Real;

plik: Text;

function f(x,y: Real): Real;

begin

f:=y-2*x/y;

end;

function yd(x: Real): Real;

begin

yd:=Sqrt(2*x+1);

end;

begin

Assign(plik,'Pr_6_2.wyn');

Rewrite(plik);

Writeln(plik,'PROGRAM 6.2');

Writeln(plik,'Zagadnienie poczatkowe dla rownania');

Writeln(plik,'rozniczkowego zwyczajnego.');

Writeln(plik,'Metoda Rungego i Kutty.');

Writeln(plik); ClrScr;

Writeln('PROGRAM 6.2. Dane do obliczen:');

Write(' - poczatek przedzialu: a = '); Readln(a);

Write(' - koniec przedzialu: b = '); Readln(b);

Write(' - liczba podprzedzialow: n = '); Readln(n);

Write(' - warunek poczatkowy: ya = '); Readln(ya);

Write(' - rodzaj metody: rodz = '); Readln(rodz);

Writeln(plik,'Poczatek przedzialu: a = ',a:13);

Writeln(plik,'Koniec przedzialu: b = ',b:13);

Writeln(plik,'Liczba podprzedzialow: n = ',n:3);

Writeln(plik,'Warunek poczatkowy: ya = ',ya:13);

Writeln(plik);

if rodz=1 then begin

R:=1; crk[1]:=1;

end;

if rodz=2 then begin

R:=2; crk[1]:=0; crk[2]:=1;

ark[2]:=1/2; brk[2,1]:=1/2;

end;

if rodz=3 then begin

R:=2; crk[1]:=1/2; crk[2]:=1/2;

ark[2]:=1; brk[2,1]:=1;

end;

if rodz=4 then begin

R:=3; crk[1]:=1/4; crk[2]:=0;

crk[3]:=3/4; ark[2]:=1/3; ark[3]:=2/3;

brk[2,1]:=1/3; brk[3,1]:=0; brk[3,2]:=2/3;

end;

if rodz=5 then begin

R:=3; crk[1]:=1/6; crk[2]:=2/3;

crk[3]:=1/6; ark[2]:=1/2; ark[3]:=1;

brk[2,1]:=1/2; brk[3,1]:=-1; brk[3,2]:=2;

end;

if rodz=6 then begin

R:=4; crk[1]:=1/6; crk[2]:=1/3;

crk[3]:=1/3; crk[4]:=1/6; ark[2]:=1/2;

ark[3]:=1/2; ark[4]:=1; brk[2,1]:=1/2;

brk[3,1]:=0; brk[3,2]:=1/2; brk[4,1]:=0;

brk[4,2]:=0; brk[4,3]:=1;

end;

if rodz=7 then begin

R:=4; crk[1]:=1/8; crk[2]:=3/8;

crk[3]:=3/8; crk[4]:=1/8; ark[2]:=1/3;

ark[3]:=2/3; ark[4]:=1; brk[2,1]:=1/3;

brk[3,1]:=-1/3; brk[3,2]:=1; brk[4,1]:=1;

brk[4,2]:=-1; brk[4,3]:=1;

end;

Write('Stopien metody: R = ');

if rodz=8 then Readln(R);

Writeln(plik,'Stopien metody: R = ',R:2);

Writeln('Wspolczynniki metody:');

Writeln(plik,'Wspolczynniki metody:');

for i:=2 to R do begin

Write(' - ark[',i:1,'] = ');

if rodz=8 then Readln(ark[i]);

Writeln(plik,' ark[',i:1,'] = ',ark[i]:13);

end;

for j:=2 to R do

for s:=1 to j-1 do begin

Write(' - brk[',j:1,',',s:1,'] = ');

if rodz=8 then Readln(brk[j,s]);

Writeln(plik,' brk[',j:1,',',s:1,'] = ',brk[j,s]:13);

end;

for i:=1 to R do begin

Write(' - crk[',i:1,'] = ');

if rodz=8 then Readln(crk[i]);

Writeln(plik,' crk[',i:1,'] = ',crk[i]:13);

end;

Writeln(plik);

Writeln(plik,'Obliczone wartosci funkcji:');

Writeln(plik,' i x[i] y[i] blad');

Writeln(plik,0:3,' ',a:13,' ',ya:13,' ',ya-ya:13);

h:=(b-a)/n; yp:=ya;

for i:=1 to n do begin

x:=a+(i-1)*h;

k[1]:=f(x,yp);

for j:=2 to R do begin

xx:=x+ark[j]*h; yy:=0;

for s:=1 to j-1 do

yy:=yy+brk[j,s]*k[s];

yy:=yp+h*yy;

k[j]:=f(xx,yy);

end;

yy:=0; xx:=x+h;

for j:=1 to R do

yy:=yy+crk[j]*k[j];

yn:=yp+h*yy;

y:=yd(xx);

Writeln(plik,i:3,' ',xx:13,' ',yn:13,' ',y-yn:13);

yp:=yn;

end;

Writeln(plik);

Close(plik);

end.

Uzyskane wyniki obliczeń dla zagadnienia (6.22) ÷ (6.24) przy wykorzystaniu zmodyfikowanej metody Eulera (6.33), metody Kutty (6.42) oraz metody Rungego-Kutty (6.43) dla h = 0.1 są następujące:

PROGRAM 6.2

Zagadnienie poczatkowe dla rownania

rozniczkowego zwyczajnego.

Metoda Rungego i Kutty.

Poczatek przedzialu: a = 0.000000E+00

Koniec przedzialu: b = 2.000000E+00

Liczba podprzedzialow: n = 20

Warunek poczatkowy: ya = 1.000000E+00

Stopien metody: R = 2

Wspolczynniki metody:

ark[2] = 5.000000E-01

brk[2,1] = 5.000000E-01

crk[1] = 0.000000E+00

crk[2] = 1.000000E+00

Obliczone wartosci funkcji:

i x[i] y[i] blad

0 0.000000E+00 1.000000E+00 0.000000E+00

1 1.000000E-01 1.095476E+00 -3.107546E-05

2 2.000000E-01 1.183298E+00 -8.246378E-05

3 3.000000E-01 1.265057E+00 -1.458713E-04

4 4.000000E-01 1.341860E+00 -2.192115E-04

5 5.000000E-01 1.414516E+00 -3.029108E-04

6 6.000000E-01 1.483638E+00 -3.986412E-04

7 7.000000E-01 1.549702E+00 -5.088738E-04

8 8.000000E-01 1.613088E+00 -6.367504E-04

9 9.000000E-01 1.674106E+00 -7.860953E-04

10 1.000000E+00 1.733012E+00 -9.615006E-04

11 1.100000E+00 1.790023E+00 -1.168462E-03

12 1.200000E+00 1.845322E+00 -1.413555E-03

13 1.300000E+00 1.899071E+00 -1.704657E-03

14 1.400000E+00 1.951410E+00 -2.051215E-03

15 1.500000E+00 2.002465E+00 -2.464571E-03

16 1.600000E+00 2.052349E+00 -2.958352E-03

17 1.700000E+00 2.101167E+00 -3.548945E-03

18 1.800000E+00 2.149017E+00 -4.256062E-03

19 1.900000E+00 2.195994E+00 -5.103428E-03

20 2.000000E+00 2.242188E+00 -6.119603E-03

PROGRAM 6.2

Zagadnienie poczatkowe dla rownania

rozniczkowego zwyczajnego.

Metoda Rungego i Kutty.

Poczatek przedzialu: a = 0.000000E+00

Koniec przedzialu: b = 2.000000E+00

Liczba podprzedzialow: n = 20

Warunek poczatkowy: ya = 1.000000E+00

Stopien metody: R = 3

Wspolczynniki metody:

ark[2] = 5.000000E-01

ark[3] = 1.000000E+00

brk[2,1] = 5.000000E-01

brk[3,1] = -1.000000E+00

brk[3,2] = 2.000000E+00

crk[1] = 1.666667E-01

crk[2] = 6.666667E-01

crk[3] = 1.666667E-01

Obliczone wartosci funkcji:

i x[i] y[i] blad

0 0.000000E+00 1.000000E+00 0.000000E+00

1 1.000000E-01 1.095445E+00 5.493202E-07

2 2.000000E-01 1.183217E+00 -1.045984E-06

3 3.000000E-01 1.264915E+00 -3.727733E-06

4 4.000000E-01 1.341648E+00 -7.118995E-06

5 5.000000E-01 1.414225E+00 -1.111322E-05

6 6.000000E-01 1.483255E+00 -1.572825E-05

7 7.000000E-01 1.549214E+00 -2.105032E-05

8 8.000000E-01 1.612479E+00 -2.721259E-05

9 9.000000E-01 1.673354E+00 -3.438848E-05

10 1.000000E+00 1.732094E+00 -4.279220E-05

11 1.100000E+00 1.788907E+00 -5.268342E-05

12 1.200000E+00 1.843973E+00 -6.437482E-05

13 1.300000E+00 1.897445E+00 -7.824217E-05

14 1.400000E+00 1.949454E+00 -9.473708E-05

15 1.500000E+00 2.000114E+00 -1.144026E-04

16 1.600000E+00 2.049528E+00 -1.378920E-04

17 1.700000E+00 2.097784E+00 -1.659920E-04

18 1.800000E+00 2.144961E+00 -1.996505E-04

19 1.900000E+00 2.191130E+00 -2.400101E-04

20 2.000000E+00 2.236356E+00 -2.884489E-04

PROGRAM 6.2

Zagadnienie poczatkowe dla rownania

rozniczkowego zwyczajnego.

Metoda Rungego i Kutty.

Poczatek przedzialu: a = 0.000000E+00

Koniec przedzialu: b = 2.000000E+00

Liczba podprzedzialow: n = 20

Warunek poczatkowy: ya = 1.000000E+00

Stopien metody: R = 4

Wspolczynniki metody:

ark[2] = 5.000000E-01

ark[3] = 5.000000E-01

ark[4] = 1.000000E+00

brk[2,1] = 5.000000E-01

brk[3,1] = 0.000000E+00

brk[3,2] = 5.000000E-01

brk[4,1] = 0.000000E+00

brk[4,2] = 0.000000E+00

brk[4,3] = 1.000000E+00

crk[1] = 1.666667E-01

crk[2] = 3.333333E-01

crk[3] = 3.333333E-01

crk[4] = 1.666667E-01

Obliczone wartosci funkcji:

i x[i] y[i] blad

0 0.000000E+00 1.000000E+00 0.000000E+00

1 1.000000E-01 1.095446E+00 -4.166814E-07

2 2.000000E-01 1.183217E+00 -7.888866E-07

3 3.000000E-01 1.264912E+00 -1.164273E-06

4 4.000000E-01 1.341642E+00 -1.567252E-06

5 5.000000E-01 1.414216E+00 -2.015520E-06

6 6.000000E-01 1.483242E+00 -2.525356E-06

7 7.000000E-01 1.549196E+00 -3.113822E-06

8 8.000000E-01 1.612455E+00 -3.800002E-06

9 9.000000E-01 1.673325E+00 -4.605952E-06

10 1.000000E+00 1.732056E+00 -5.557602E-06

11 1.100000E+00 1.788861E+00 -6.685732E-06

12 1.200000E+00 1.843917E+00 -8.027086E-06

13 1.300000E+00 1.897376E+00 -9.625679E-06

14 1.400000E+00 1.949370E+00 -1.153435E-05

15 1.500000E+00 2.000014E+00 -1.381663E-05

16 1.600000E+00 2.049407E+00 -1.654898E-05

17 1.700000E+00 2.097638E+00 -1.982352E-05

18 1.800000E+00 2.144785E+00 -2.375129E-05

19 1.900000E+00 2.190919E+00 -2.846617E-05

20 2.000000E+00 2.236102E+00 -3.412970E-05

*

Podstawowa wada klasycznych metod Rungego-Kutty, wynikająca z konieczności wielokrotnego obliczania prawych stron równania różniczkowego, została wyeliminowana w zmodyfikowanych metodach Rungego-Kutty [31], opracowanych dla równań różniczkowych postaci:

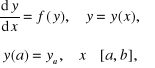
(6.57)

takich jakie występują najczęściej w numerycznej mechanice płynów. Algorytm zmodyfikowanych metod Rungego-Kutty jest następujący:

(6.58)

Jedną z najbardziej popularnych zmodyfikowanych metod Rungego-Kutty jest metoda określana współczynnikami:

(6.59)

odznaczająca się dobrą stabilnością numeryczną.

{Program 6.3}

uses Crt;

var

i,j,n: Integer;

a,b,h,x,xx,y,ya,yn,yp,yst: Real;

alf: array[1..5] of Real;

plik: Text;

function f(x,y: Real): Real;

begin

f:=y;

end;

function yd(x: Real): Real;

begin

yd:=Exp(x);

end;

begin

Assign(plik,'Pr_6_3.wyn');

Rewrite(plik);

Writeln(plik,'PROGRAM 6.3');

Writeln(plik,'Zagadnienie poczatkowe dla rownania');

Writeln(plik,'rozniczkowego zwyczajnego.');

Writeln(plik,'Zmodyfikowana metoda Rungego i Kutty.');

Writeln(plik); ClrScr;

Writeln('PROGRAM 6.3. Dane do obliczen:');

Write(' - poczatek przedzialu: a = '); Readln(a);

Write(' - koniec przedzialu: b = '); Readln(b);

Write(' - liczba podprzedzialow: n = '); Readln(n);

Write(' - warunek poczatkowy: ya = '); Readln(ya);

Writeln(plik,'Poczatek przedzialu: a = ',a:13);

Writeln(plik,'Koniec przedzialu: b = ',b:13);

Writeln(plik,'Liczba podprzedzialow: n = ',n:3);

Writeln(plik,'Warunek poczatkowy: ya = ',ya:13);

Writeln(plik);

alf[1]:=1/4; alf[2]:=1/6;

alf[3]:=3/8; alf[4]:=1/2;

alf[5]:=1;

for i:=1 to 5 do

Writeln(plik,' alfa[',i:1,'] = ',alf[i]:13);

Writeln(plik);

Writeln(plik,'Obliczone wartosci funkcji:');

Writeln(plik,' i x[i] y[i] blad');

Writeln(plik,0:3,' ',a:13,' ',ya:13,' ',ya-ya:13);

h:=(b-a)/n; yp:=ya;

for i:=1 to n do begin

x:=a+(i-1)*h;

yst:=yp;

for j:=1 to 5 do begin

yn:=yp+h*alf[j]*f(x,yst);

yst:=yn;

end;

xx:=x+h; y:=yd(xx);

Writeln(plik,i:3,' ',xx:13,' ',yn:13,' ',y-yn:13);

yp:=yn;

end;

Writeln(plik);

Close(plik);

end.

Program 6.3 jest przeznaczony do rozwiązywania zagadnienia (6.57) przy wykorzystaniu zmodyfikowanej metody Rungego-Kutty (6.58) - (6.59). W charakterze przykładu rozwiązano zagadnienie:

w przedziale
przyjmując
rozwiązanie dokładne
Otrzymane wyniki porównano z wynikami uzyskanymi za pomocą programu 6.2. Dokładność zmodyfikowanej metody Rungego-Kutty (6.58) - (6.59) jest tego samego rzędu co dokładność klasycznych metod Rungego-Kutty trzeciego i czwartego rzędu, dla których trzeba jednak wielokrotnie obliczać prawe strony funkcji

PROGRAM 6.3

Zagadnienie poczatkowe dla rownania

rozniczkowego zwyczajnego.

Zmodyfikowana metoda Rungego i Kutty.

Poczatek przedzialu: a = 0.000000E+00

Koniec przedzialu: b = 5.000000E+00

Liczba podprzedzialow: n = 10

Warunek poczatkowy: ya = 1.000000E+00

alfa[1] = 2.500000E-01

alfa[2] = 1.666667E-01

alfa[3] = 3.750000E-01

alfa[4] = 5.000000E-01

alfa[5] = 1.000000E+00

Obliczone wartosci funkcji:

i x[i] y[i] blad

0 0.000000E+00 1.000000E+00 0.000000E+00

1 5.000000E-01 1.650635E+00 -1.913495E-03

2 1.000000E+00 2.724595E+00 -6.313301E-03

3 1.500000E+00 4.497311E+00 -1.562237E-02

4 2.000000E+00 7.423419E+00 -3.436252E-02

5 2.500000E+00 1.225335E+01 -7.085889E-02

6 3.000000E+00 2.022581E+01 -1.402733E-01

7 3.500000E+00 3.338543E+01 -2.699735E-01

8 4.000000E+00 5.510714E+01 -5.089940E-01

9 4.500000E+00 9.096177E+01 -9.446364E-01

10 5.000000E+00 1.501447E+02 -1.731497E+00

PROGRAM 6.2

Zagadnienie poczatkowe dla rownania

rozniczkowego zwyczajnego.

Metoda Rungego i Kutty.

Poczatek przedzialu: a = 0.000000E+00

Koniec przedzialu: b = 5.000000E+00

Liczba podprzedzialow: n = 10

Warunek poczatkowy: ya = 1.000000E+00

Stopien metody: R = 3

Wspolczynniki metody:

ark[2] = 5.000000E-01

ark[3] = 1.000000E+00

brk[2,1] = 5.000000E-01

brk[3,1] = -1.000000E+00

brk[3,2] = 2.000000E+00

crk[1] = 1.666667E-01

crk[2] = 6.666667E-01

crk[3] = 1.666667E-01

Obliczone wartosci funkcji:

i x[i] y[i] blad

0 0.000000E+00 1.000000E+00 0.000000E+00

1 5.000000E-01 1.645833E+00 2.887937E-03

2 1.000000E+00 2.708767E+00 9.514467E-03

3 1.500000E+00 4.458180E+00 2.350946E-02

4 2.000000E+00 7.337421E+00 5.163548E-02

5 2.500000E+00 1.207617E+01 1.063225E-01

6 3.000000E+00 1.987537E+01 2.101714E-01

7 3.500000E+00 3.271154E+01 4.039129E-01

8 4.000000E+00 5.383774E+01 7.604087E-01

9 4.500000E+00 8.860795E+01 1.409182E+00

10 5.000000E+00 1.458339E+02 2.579243E+00

PROGRAM 6.2

Zagadnienie poczatkowe dla rownania

rozniczkowego zwyczajnego.

Metoda Rungego i Kutty.

Poczatek przedzialu: a = 0.000000E+00

Koniec przedzialu: b = 5.000000E+00

Liczba podprzedzialow: n = 10

Warunek poczatkowy: ya = 1.000000E+00

Stopien metody: R = 4

Wspolczynniki metody:

ark[2] = 5.000000E-01

ark[3] = 5.000000E-01

ark[4] = 1.000000E+00

brk[2,1] = 5.000000E-01

brk[3,1] = 0.000000E+00

brk[3,2] = 5.000000E-01

brk[4,1] = 0.000000E+00

brk[4,2] = 0.000000E+00

brk[4,3] = 1.000000E+00

crk[1] = 1.666667E-01

crk[2] = 3.333333E-01

crk[3] = 3.333333E-01

crk[4] = 1.666667E-01

Obliczone wartosci funkcji:

i x[i] y[i] blad

0 0.000000E+00 1.000000E+00 0.000000E+00

1 5.000000E-01 1.648438E+00 2.837707E-04

2 1.000000E+00 2.717346E+00 9.356370E-04

3 1.500000E+00 4.479375E+00 2.313708E-03

348 6. Równania różniczkowe zwyczajne i całkowe

6.1. Zagadnienia początkowe dla równań różniczkowych zwyczajnych 365

---