020 021

20 Piotr Sajpel Krzysztof Stroiński

Współczynniki A_x.....A_m wyznaczamy ze wzoru (1.29) lub (1.31),

natomiast współczynniki B\.....B_p obliczamy ze wzorów:

B_r

L(s)(s-s_ny

M(s)

Vi =

ds

L(s)(s-s„f

M(s)

B -LfL

2 ds¹

1 d'

B. ds‘

L(s)(s~s„ f M(s)

L(s)(s ~ s_n)^ł M{s)

(1.33)

Podany sposób rozkładu na ułamki proste można poszerzyć na przypadki, w których występuje kilka wielokrotnych miejsc zerowych.

1.5. Wyznaczanie transmitancji podstawowych połączeń elementów [2]

Przy analizie budowy poszczególnych układów automatyki spotykamy się z zróżnicowanymi połączeniami między elementami tworzącymi te układy. Jednakże wszystkie dają się sprowadzić do trzech podstawowych rodzajów.

1.5.1. Połączenie szeregowe elementów o jednym wejściu i wyjściu (rys. 1.4)

Na podstawie definicji transmitancji. którą podaliśmy wcześniej, możemy napisać:

y(s) ₌ b(s) a(s) x(s) b(s) a(s) x(s)

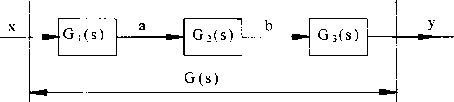
Rys. 1.4. Szeregowe połączenie elementów

Uzyskany wynik możemy uogólnić na n elementów. Ogólnie, transmitancja szeregowego połączenia elementów jest równa iloczynowi transmitancji ty ch elementów.

1.5.2. Połączenie równolegle elementów o jednym wejściu i wyjściu (rys. 1.5)

Zastępcza transmitancja takiego układu przyjmie postać:

y(s) ^ a(s) + b(s)-c(s) ₌ a{s) _| b(s) c(s)

;t(s)    *(s)    ;c(s) x(s) x(s)

G(s) = G_l(s) + G₂(s)~G_i(s)    (1.35)

Ogólnie, transmitancja równoległego połączenia elementów jest równa algebraicznej sumie (z uwzględnieniem znaków) transmitancji tych elementów.

Jeżeli w dowolnej gałęzi schematu blokowego nie występuje żaden blok

0    określonej transmitancji, to transmitancja takiej gałęzi równa się 1 (wejście

1    wyjście tej gałęzi jest takie same).

Rys 1.5. Równoległe połączenie elementów