analiza07a

21.    Podać definicję pochodnej kierunkowej, pochodnej cząstkowej i gradientu funkcji wielu zmiennych. Jaką własność ma wektor gradientu funkcji.

22.    Podać definicję różniczki odwzorowania / : R'¹ —> R* i jej związek z pochodnymi cząstkowymi.

23.    Podać warunek konieczny i dostateczny istnienia ekstremum funkcji wielu zmiennych klasy C².

24.    Sformułować twierdzenie Lagrange’a o ekstremum warunkowym funkcji różniczkowalnej. Opisać metodę wyznaczania największej i najmniejszej wartości takiej funkcji na zbiorze zwartym.

25.    Podać definicję funkcji wypukłej i opisać jej własności. Sformułować twierdzenia o równoważnych określeniach wypukłości.

26.    Sformułować twierdzenia o wartościach funkcji wypukłej na zbiorze zwartym i wypukłym.

27.    Sformułować zagadnienie Cauchy‘ego dla układu równań różniczkowych x' = f(t,x). Sformułować twierdzenie o istnieniu i jednoznaczności rozwiązania zagadnienia Cauchy‘ego.

28.    Podać definicję stopy wzrostu funkcji i elastyczności funkcji. Opisać ich własności.

Pytania dodatkowe - dowody twierdzeń

1.    Udowodnić warunek Fermata dla ekstremum funkcji jednej zmiennej.

2.    Udowodnić podstawowe własności funkcji £/(x).

3.    Wykazać twierdzenie o postaci funkcji prostej nieujemnej.

4.    Wykazać twierdzenie o jednostajnej ciągłości funkcji z ograniczoną pochodną.

5. Wykazać, że

R

Je ^x2dx = \/7r lub B(x,y)

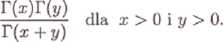
6.    Udowodnić twierdzenie o związku wypukłości funkcji i wypukłości jej nadwykresu.

7.    Udowodnić twierdzenie Bolzano-Weierstrassa.

8.    Udowodnić, że zbiór A C R jest spójny w't,edy, gdy jest przedziałem.

9.    Udowodnić twierdzenie o własnościach funkcji ciągłej określonej na zbiorze zwartym (spójnym).

10.    Udowodnić, że R jest przestrzenią zupełną.

11.    Udowodnić twierdzenie o równoważnych określeniach ciągłości przekształcenia przestrzeni metrycznych.

12.    Udowodnić zasadnicze twierdzenie dla całki Lebcsgue’a.

13.    Udowodnić kryterium całkowe zbieżności szeregu liczbowego.

14.    Udowodnić twierdzenie o równoważnym określeniu wypukłości dla funkcji klasy C^l lub C².

Prowadzący przedmiot dr ‘Wojciech Hyb Katedra Zastosowań Matematyki