skanuj0021

4.6. WYWAŻANIE MASZYN I MECHANIZMÓW 177

1, ..., 6) i zakreskowano półpłaszczyzny, w których warunki (4.119) nie^- są spełnione. Po odrzuceniu tych półpłaszczyzn zostaje tzw. simpleks, będący obszarem rozwiązań dopuszczalnych.

Dla przykładu podamy, jak się wykreśla linię m? = 0. Dla m-j = 0

_m _ _ 10/04    _    ,    ₉

^m6 “    0,033    304,2,

dla mg ^W1 ⁼

= 0

10,04

1,033

9,72.

Obrazem rodziny równań 2(mi, m§) = const są linie proste tworzące z osią mę (rys. 4.45) kąt 45 . Prowadząc taką linię przez naroże simpleksu, najbliższe do początku układu, znajduje się, że rozwiązanie optymalne jest na przecięciu linii - 0 i linii m^ = 0; z drugiego równania układu (4.119) jest m-j = 9,719. Po wstawieniu tych wartości do pozostałych równań (4.119) otrzymuje się nr\ = 9,719, m2 - 0, ^3 =

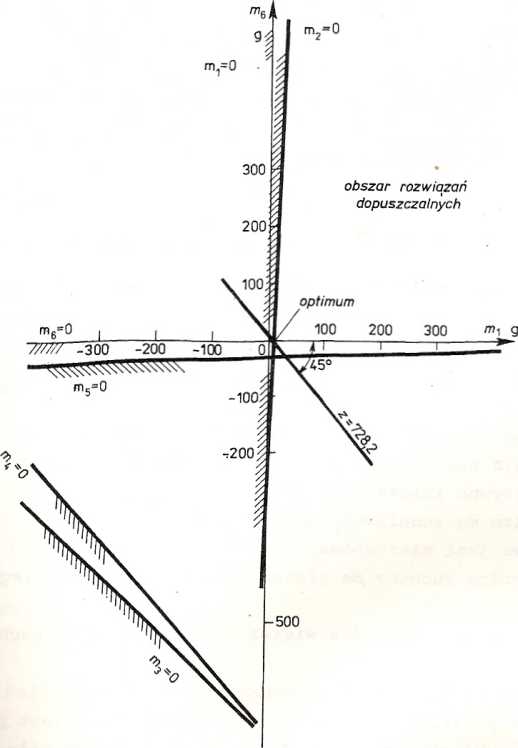
Rys. 4.45