Strona0119

119

układu jednorodnego opisują drgania swobodne nietłumione, które pominięto w dalszych rozważaniach (w układach rzeczywistych występuje pewne tłumienie i drgania swobodne zanikają, z tego względu można rozwiązanie drgań swobodnych pominąć), a zajęto się rozwiązaniem szczególnym układu niejednorodnego. Rozwiązania te opisują drgania, które nazywano drganiami wymuszonymi.

Ponieważ do układów liniowych stosuje się zasadę superpozycji, można rozważać drgania wymuszone kolejno siłami przyłożonymi do poszczególnych punktów materialnych, a następnie otrzymane rozwiązania dodawać.

Rozwiązania równań różniczkowych (5.39) lub (5.40) można przedstawić jako rozłożenia na postacie własne:

n

=T,^au9j(0

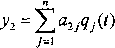
n

(5.41)

gdzie: a-y - amplitudy znormowanych postaci własnych drgań (lub warunki normowania (5.26)), a funkcje ąjf) wyznacza się z układu równań różniczkowych ruchu:

j=I

n

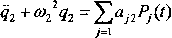
(5.42)

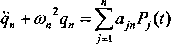
gdzie: co\,..., co„ - częstości drgań własnych.

Jeżeli siły P/t) mają postać wymuszeń harmonicznych w postaci:

(5.43)

P\-P_Q\ sin ot, P₂ ~ Pq₂ sin cot,..., P_n~ P_0n sin ruf

to rozwiązaniem dowolnego z równań (5.42) jest następująca suma: