129(1)

Obliczyć długość łuku krzywej:

644.    9>'² = 4(3—.\')³ między punktami przecięcia z osią Oy

645.    Asteroidy x = «cos³?, y = nsin³?

⁰) między prostymi x =

—a

e^a -e

.    ci (

646.    Linii łańcuchowej y =- ^ \ i x = 0

647.    2y — X²—2 między punktami przecięcia z osią Ox 648*. y = lnx między prostymi x — | 3 i x = ]/8 649. Kardioidy o = a(\+cos<p)

65(L Pierwszego zwoju spirali Archimedesa o = acp

C²    ę²

651*. Ewoluty elipsy x — — cos³?, y = sin³?

Obliczyć obwód figury ograniczonej liniami:

652. x² = (j+1)³ i y = 4 653*. y^z = 2px i 2x = p

§ 7. Pole powierzchni obrotowej

Jeżeli powierzchnia powstaje na skutek obrotu łuku AM krzywej płaskiej wokół osi Ox (rys. 118), to różniczka pola tej powierzchni jest równa polu powierzchni bocznej kołowego stożka ściętego, o tworzącej dl i promieniach podstawy y i y-'~dy

n(2y-{-dy)dl z. lny dl

d_S= ^y+^y+^ldi

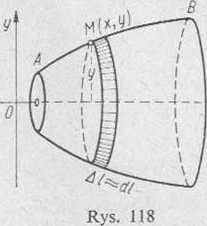
a pole powierzchni, utworzonej przez obrót łuku AB, jest określone wzorem

(Ą)    (-5)

(a)

(a)

ó’ - J dS = 2n J ydl    (1)

przy czym (A) i (B) oznaczają wąrtości obranej zmiennej całkowania w punktach A i B, a dl— różniczkę łuku krzywej.

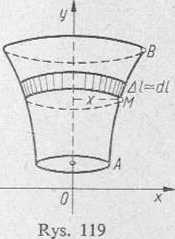
Jeśli obrót łuku AB odbywa się wokół osi Oy (rys. 119), to

<fl>    (fl)

dS k 2nxdl,    S -- f dS == 2jc f xdl    (2)

(a)    (/O

654. Obliczyć pola powierzchni powstałych przez obrót wokół osi Ox:

2

1) łuku paraboli sześciennej y = x³, zawartego między prostymi x — —-

2    j^2    y.2

i ,v = y, 2) asteroidy x = acos³f, y = tfsin³r, 3) elipsy    = 1,

a> b.

Rozwiązanie: 1) Rysując łuk paraboli między punktami A i B, 2

gdzie x = ± y (rys. 120), widzimy, że powierzchnia utworzona przez obrót

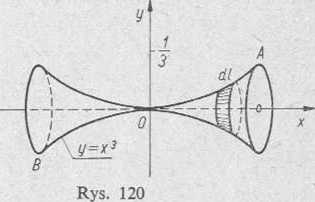
tego łuku wokół osi Ox składa się z dwóch równych części. Dlatego po uwzględnieniu wzoru (1), mamy

A    ²

3    __ 3

S = 2 • 2n I y | 1 -j (y’)²dx = 4rt j x³)/1 -p9jc⁴<ijc ó    o

Aby obliczyć tę całkę, podstawiamy 1+9x* = t, skąd 36x-dx — dt

25    2

oraz = 1 dla x = 0 i t₂"— ^ dla x — ^ . Mamy więc

S = 4rr

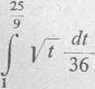
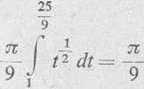
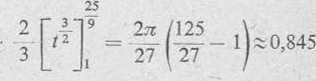
261