132 2

262 XII. Wyrażenia nieoznaczone

limg(x) = 0. Wówczas oczywiście lim—=0. Stosując przeksztalcenie(¹)

x-a    x-¹aJ\X)

.. _w , sW

/w?w=—

7w

otrzymujemy iloraz funkcji g(x) przez l//(x), który w punkcie x=a jest wyrażeniem nieoznaczonym postaci g. Do obliczania granic tego ilorazu możemy stosować metody podane w rozdziale V oraz w § 12.1.

Zadanie 12.9. Wyznaczyć lim (x-i7t)tgx.

Rozwiązanie. Mamy tu dla x=-£tc wyrażenie postaci O oo; przekształcamy j_e jak wyżej:

1

Ctg X

x—\n x—\k (¹-ł¹)tg¹=-

tg X

Do ostatniego wyrażenia stosujemy regułę de L’Hospitala:

X — ^71    1

lim -= lim -= lim ( — sin x)= — 1.

ctg X    1    x-¹i¹

sin² x

Zadanie 12.10. Obliczyć lim x^k ln x przy k> 0.

x-¹ + 0

Rozwiązanie. Stosując podstawienie

1    1

x=—,    skąd    z =    —,

Z    X

mamy lim z= + oo, a więc

x~¹ + oo

mi

z    —ln z

lim x ln x= lim —^-= lim —j—,

x-¹ + 0    z-¹ + oo Z    + oo Z

lim x^klnx=0 dla    k>0.

x-» + 0

Na podstawie zadania 12.8 wnioskujemy, że (12.3.1)

§ 12.4. WYRAŻENIA NIEOZNACZONE POSTACI oo - oo

Rozpatrzmy wyrażenie postaci f(x)-g(x) takie, że gdy x-+a, to/(a)-> + oo i g(x)-> ^ ₊ C30 albo /(a)-» —oo i g(x)->-co.

Zastosujemy podstawienia:

^{u(x) =} 7Tw    ^t,W = -7T

/(*)    fW

wówczas przy x->a jest h(a)-+0, p(a)-»0. Otrzymamy więc

1

f(x)-g(x)=-—

u(x)

I

v(x)

v(x)-u(x)

u(x)v(x)

Ostatecznie wyrażenie przy x=a jest postaci 2, możemy więc do niego stosować poznane już metody.

Zadanie 12.11. Wyznaczyć

lim

1_ l

x — 1 ln a:

Rozwiązanie. Mamy tu wyrażenie postaci co —oo. Odejmując ułamki otrzymujemy . lnx—a + 1

wyrażenie ^ ‘~|) ]— ’ które w punkcie a = 1 jest wyrażeniem nieoznaczonym postaci 2.

Przy obliczaniu granicy otrzymanego wyrażenia stosujemy dwukrotnie regułę de L’Hos-pitala:

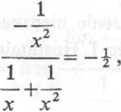
1

, --1

ln A — A + l    A

hm --=lim -=lim

x-l (A— 1) ln A    1 je-* 1

ln A + l--

A

^czyli ostatecznie

lim

A-l

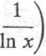
§ 12.S. WYRAŻENIA NIEOZNACZONE POSTACI co⁰, 0°, 1“

, Niech będą dane funkcje w(a) i v(x) określone w pewnym sąsiedztwie (ewentualnie postronnym) punktu x=a, przy czym w(a)>0 dla wszystkich a j=a należących do ^te8o otoczenia. Weźmy pod uwagę wyrażenie

^fl)    f{x)=[u(x)Y^x\

*° Jeżeli przy x->a mamy u(a)-> + oo i jednocześnie u(a)->0, to mówimy, że wyra-^le (1) w punkcie a — a jest wyrażeniem nieoznaczonym postaci co⁰.

1

Przekształcenie to ma miejsce dla /(x)#0. Ponieważ lim /(x)= + co lub lim f(x)=~ ’

x-»«    ¹-•«

otoczenie punktu x=a możemy tak zwęzić, żeby było f(x)ć 0 dla każdego x należącego dono otoczenia.