135 3

268 XII. Wyrażenia nieoznaczone

268 XII. Wyrażenia nieoznaczone

\ Ig (*x/a)	/
j	12.74. lim I	2--)
/		a

12.73. lim^l--^

12.75.    lim (x-l)‘^,/(^,n2(*^-l)>.

*-»i +o

12.76.    Wykazać, że pole S wycinka kołowego o małym kącie środkowym a jest w nr

bliżeniu równe \bh, gdzie b jest długością cięciwy AB, a h strzałką CD (rys. 12.1).    '

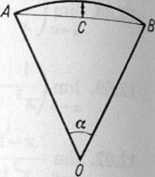
Rys. 12.1

12.77. Wykazać, że przy a->0 mamy V1 +a— 1 —    —ia² i stąd VT+a«l+ja, z dokładnością do ja².

12.78.    Wykazać, że przy a-*0 mamy Vl +a — 1 — |a« — ja² i stąd \/T+a«l+3a, z dokładnością do ja².

12.79.    Dwa kąty zmienne a i fi mają stałą sumę tx + fi=$n.

Obliczyć, do jakiej granicy dąży ułamek

gdy

4

sin a - sin fi

sin (a—/?)

12.80. Dwa kąty zmienne a i fi mają stałą sumę a + fiObliczyć, do jakiej granicy dąży iloczyn sin a tg fi, gdy a->0.

BADANIE PRZEBIEGU ZMIENNOŚCI FUNKCJI WYKŁADNICZYCH I LOGARYTMICZNYCH

§ 13.1. BADANIE PRZEBIEGU ZMIENNOŚCI FUNKCJI WYKŁADNICZEJ I LOGARYTMICZNEJ

Dla wygody zapisu będziemy często oznaczali badane funkcje przez f(x).

Zadanie 13.1. Zbadać przebieg zmienności funkcji y=xe~^x.

Rozwiązanie. Funkcja jest określona dla wszystkich wartości x.

Obliczmy pierwszą pochodną

y' = 1 ■ e~^x+xe~^x( -1) =e"*(l -x).

Pochodna jest równa zeru, gdy jc=1; wówczas /(l) = e~‘.

Po powtórnym zróżniczkowaniu otrzymujemy

y" = e~^x(x-2).

Druga pochodna jest równa zeru, gdy x = 2; wtedy /(2) = 2e~².

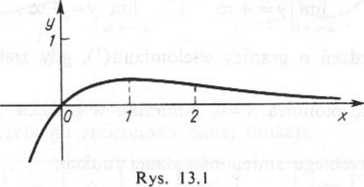
Następnie obliczmy granice funkcji przy jr-> + oo i przy x-* — co:

Prze-

lim xe ^x= lim — = 0(‘), lim xe~^x= -co.

x— + co    x— cq &    x— - co

krzywa ma jednostronną asymptotę poziomą y = 0, maksimum w punkcie x=l i punkt

8'ęeia, gdy x = 2.

^(l) Patrz

wzór (12.2.4).