143 2

284

XIV. Przybliżone rozwiązywanie równań i układów

§ 14.2. Metoda stycznych

285

W taki sam sposób możemy znaleźć dalsze przybliżenia x₂, x₃, x„ poszu]^ nego pierwiastka £ równania f(x) = Q. Aby ocenić błąd otrzymanego przybliżenia, tz_Q' wartość bezwzględną różnicy pomiędzy przybliżoną wartością pierwiastka x„ a doklad_n wartością £ pierwiastka, stosujemy wzór

(14.1.2)    ’

w którym k oznacza kres dolny bezwzględnej wartości pochodnej f'{x) w rozpatrywanym przedziale.

Zadanie 14.1. Dane jest równanie

f(x) = x³+x-5 = 0,

które ma pierwiastek rzeczywisty £ zawarty pomiędzy a= 1, a b=2, gdyż/(a)=/(l) = -3, _a f(b)=f(2) = 5. Obliczyć ten pierwiastek.

Rozwiązanie. Stosując wzór (14.1.1) otrzymujemy

2-1

*1 = 1^—( — 3) ■

:=¥=U7...

5—(—3)

Chcąc znaleźć dokładniejszą wartość pierwiastka obliczamy np./(l,4) = -0,86. Mamy teraz węższy przedział <a_t = 1,4, b=2}, gdyż

/(ai)=/(*i)=-0,86,    f{b)=f{x₂) = S.

Postępujemy jak wyżej i ze wzoru (14.1.1) otrzymujemy dokładniejszą wartość pierwiastka, którą oznaczamy przez x₂:

2-1,4

x₂ = 1,4 —(—0,86) ■

5+0,86

= 1,49.

Przyjmijmy jako wartość przybliżoną wartość x₂x%. Aby ocenić dokładność tego wyniku za pomocą nierówności (14.1.2), zauważmy, że f'(pć) = 2>x² +1, a więc kres dolny wartości bezwzględnej pochodnej w przedziale <1,2) wynosi k=f'{\) = Ą\ dalej obliczamy

/(|)=i^L+!-⁵=-i-

Otrzymujemy więc |x₂-^|^g2_<0,032.    .Iggfc

Tak więc wartość £ zawiera się w granicach | < £ < 1,532 (radzimy sporządzić s

i wyjaśnić, dlaczego £>$).

§ 14.2. METODA STYCZNYCH (NEWTONA)

Zakładamy, że funkcja y=f(x) ma pierwszą i drugą pochodną różną od zera w P dziale a.    j_?.

Metoda stycznych (lub Newtona) różni się od metody reguła falsi tym, że zanu ^ ciwy prowadzimy styczną do krzywej w jednym z końcowych punktów przedzi >

^ybltfoną wartość pierwiastka przyjmujemy odciętą x_x punktu, w którym styczna {leońcu łuku przecina oś Ox.

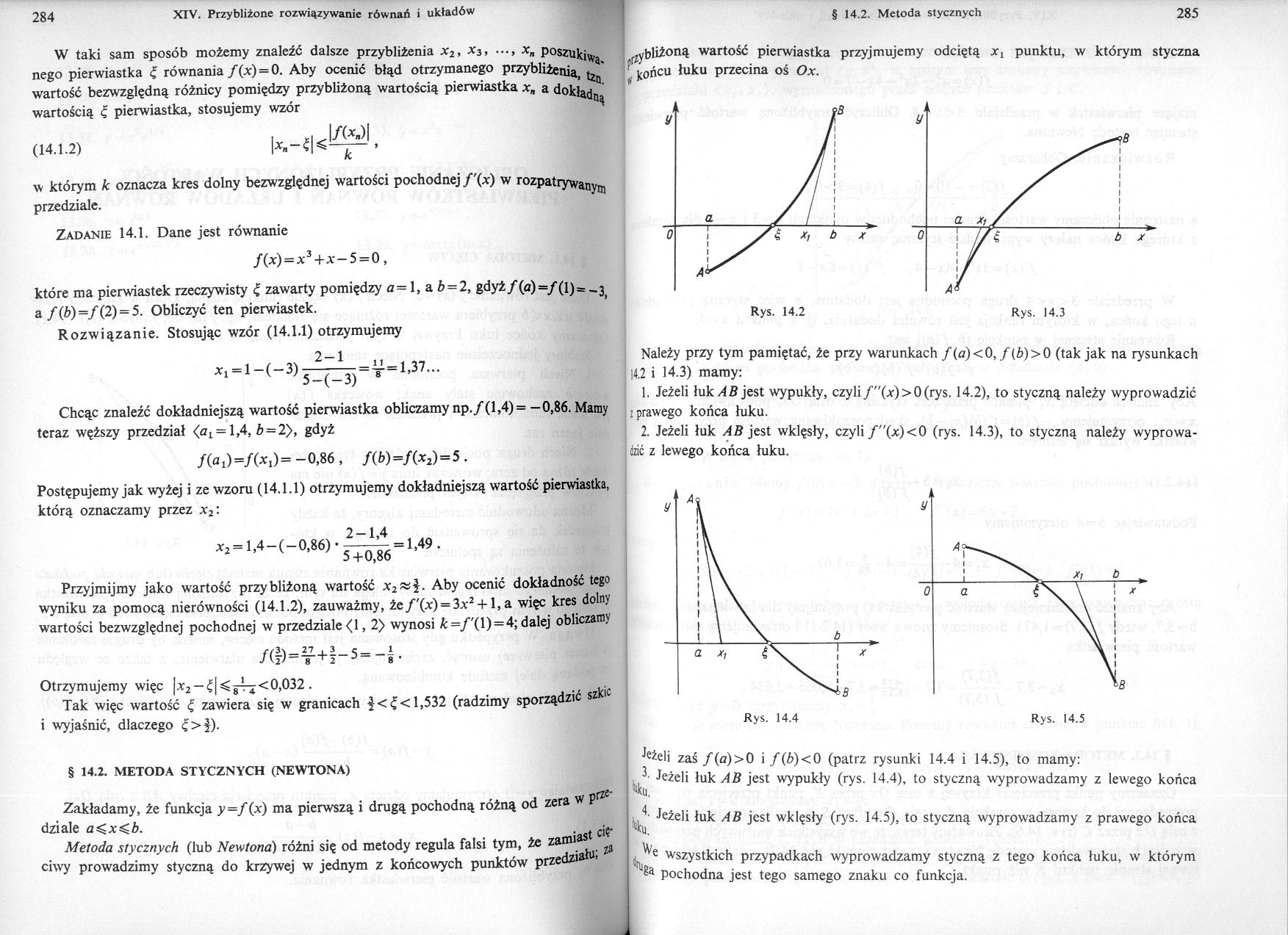
Należy przy tym pamiętać, że przy warunkach f(d)<0, f(b)>0 (tak jak na rysunkach 14.2 i 14.3) mamy:

1.    Jeżeli łuk AB jest wypukły, czyli /"(x)>0(rys. 14.2), to styczną należy wyprowadzić i 1 prawego końca łuku.

2.    Jeżeli łuk AB jest wklęsły, czyli /"(*)<0 (rys. 14.3), to styczną należy wyprowadzić z lewego końca łuku.

Rys. 14.4

Rys. 14.5

^Jeże,i zaś/(a)>0 i f(b)<0 (patrz rysunki 14.4 i 14.5), to mamy: leżeli łuk AB jest wypukły (rys. 14.4), to styczną wyprowadzamy z lewego końca

Jeżeli łuk AB jest wklęsły (rys. 14.5), to styczną wyprowadzamy z prawego końca

3, ku.

4.

V

W,

H ^{e Wsz}y^stkich przypadkach wyprowadzamy styczną z tego końca łuku, w którym pochodna jest tego samego znaku co funkcja.