144 2

286 XIV. Przybliżone rozwiązywanie równań i układów

Zadanie 14.2. Dane jest równanie

f(x) = x³- 2x² —4x-l = 0

mające pierwiastek w przedziale 3<x<4. Obliczyć przybliżoną wartość pierwiastka stosując metodę Newtona.

Rozwiązanie. Obliczamy

/(3)=—10<0,    /(4) = 9>0,

a następnie obliczamy wartości drugiej pochodnej w punktach x=3 i x = 4 dla ustalenia, z którego końca należy wyprowadzić styczną; mamy

/'(*) = 3x² — 4x—4 ,    f"(x) = 6x - 4 .

W przedziale 3<x<4 druga pochodna jest dodatnia, a więc styczną prowadzimy z tego końca, w którym funkcja jest również dodatnia, tj. z punktu x=4.

Równanie stycznej w punkcie (b,f(b)) jest

y-m=rmx-b).

Aby znaleźć odciętą x_t punktu przecięcia stycznej z osią Ox, podstawiamy y=0 oraz x = Xi‘, otrzymujemy -f (b) = f'(b)(x_l - b), skąd poszukiwana wartość przybliżona pierwiastka wyrazi się wzorem

(14.2.1)

. Ab)

*^mb-m

Podstawiając b=4 otrzymujemy

A    Ą 9 cn

/'(⁴)

*i = ⁴-777^ = ⁴-5ś = ³>⁶7 •

Aby znaleźć dokładniejszą wartość pierwiastka, przyjmijmy dla łatwiejszego rachunku b=3,7; wtedy/(3,7) = 1,473. Stosujemy znowu wzór (14.2.1) i otrzymujemy dokładniejszą wartość pierwiastka

*2 = 3,7-

/(3,7) /'( 3,7)

= 3,7 -    =3,7 - 0,066 = 3,634 .

§ 14.3. METODA KOMBINOWANA

Oznaczmy punkt przecięcia krzywej z osią Ox przez A, punkt przecięcia stycznej poprowadzonej do krzywej w punkcie A z osią Ox przez 5, a punkt przecięcia cięciwy AB z osią Ox przez C (rys. 14.6). Zauważmy teraz, że we wszystkich możliwych przypadkach, w których stosowaliśmy metodę Newtona (patrz rysunki w § 14.2), punkt S leży po przeciwnej stronie punktu K niż punkt C.

Ha podstawie tej uwagi, stosując obie metody (reguła falsi i metodę Newtona) kolejno, możemy zwęzić przedział <a, 6>, w którym leży szukany pierwiastek równania, (jo przedziału <x,, x\y, wyznaczonego przez odcięte punktów S i C.

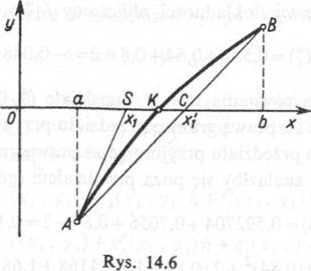
Jest to tzw. metoda kombinowana. Oczywiście, przy tej metodzie zakładamy tak samo, te pierwsza i druga pochodna zachowują stały znak w przedziale (a, by.

Zadanie 14.3. Obliczyć przybliżoną wartość pierwiastka równania

(1)    •    f(x)=x³+x²+x-2=0,

który znajduje się w przedziale (0, 1).

Rozwiązanie. Mamy /(0)= — 2, /(1) = 1. Obliczamy wartości pochodnych:

/'(*)=3*² + 2x +1 ,    /"(*) = 6x+2,

mamy więc

/(0)= —2 , /(1)= 1 ,    /'(0)=1 , /'(!)=6 ,    /"(O) = 2 , /"(1) = 8 .

Obliczamy pierwsze przybliżenie pierwiastka metodą reguła falsi, prowadząc prostą przez punkty ,4(0, -2) i 5(1, 1); mamy

„ 1 +2

y+2 =    - (■£ - 0),    czyli y+2 = 3x.

Podstawiając y=0 otrzymujemy x_i=~.

Następnie stosujemy metodę Newtona. Piszemy równanie stycznej w punkcie 5(1, 1); mamy

“ 1 =/'(!)(*—l), czyli y — H=6(* — 1).

Podstawiając y = 0 znajdujemy x\ =|.

Możemy więc teraz twierdzić, że pierwiastek naszego równania (1) znajduje się w przepale (|, |) o długości |, czyli w przedziale (0,666..., 0,833...).

Jeżeli ta dokładność nie jest wystarczająca, to obliczamy np. f (y^); jeżeli okaże się /(^)>0, to pierwiastek będzie się znajdować w przedziale (§, ^), a jeżeli /(^)<0, to