146 2

290 XIV. Przybliżone rozwiązywanie równań i układów

>^0,5^0,8. Tak więc możliwe punkty przecięcia się krzywych leżą w pierwszej ćwi_art (rys. 14.7).

Wykonajmy teraz kilka podstawień wartości x w równaniu (2) i wartości y w równaj (3). Dla równania (2) mamy

X	l	2
y	5	0,75

a dla równania (3) mamy

*	1	2
X	±1	±3,8

Ponieważ przy x rosnącym od 1 do 2 pierwsza funkcja maleje od y=5 do y=0,75, a przy * rosnącym od 1 do 3,8 druga funkcja rośnie od y= 1 do y = 2, więc musi istnieć jedno rozwią. zanie z wartością * pomiędzy 1 a 2.

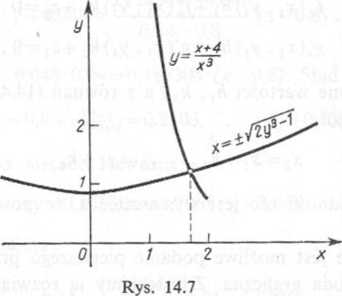
Aby otrzymać dokładniejsze oszacowanie, wykonajmy jeszcze dodatkowe obliczenia wartości y z pierwszej funkcji podstawiając x=l,5; mamy

X	1,5
y	1,6

Otrzymaną przybliżoną wartość yx 1,6 podstawimy do drugiej funkcji; otrzyn^,uJ^etn' x = ^/2•1,6³ — 1 «2,7. Wartość ta odbiega jeszcze znacznie od *=1,5. Powiększa.m> . wartość * do * = 1,7, wtedy z pierwszej funkcji mamy y~5,7:4,9«1,2, a podsta ^ tę wartość do drugiej funkcji otrzymujemy * = \fe • 1,2³ — 1«1,6. Jesteśmy już więc w przyjąć jako pierwsze przybliżenie

yi = l,2.

*i = l,7,

Obliczamy pochodne cząstkowe lewych stron (1) i ich wartości w punkcie (1,7; 1,2): /;=3*²y-l,    /_x'(l,7; 1,2) = 9,40 , /;=*³,    //(1,7; 1,2) = 4,91,

g_x=2x,    g'_x{\,7;1,2) = 3,4,    g'_y=-6y²,    g'_y( 1,7; 1,2)=-8,64 .

^ wzoru (14.4.2) otrzymujemy wartości

«!=/(l,7; 1,2) = 0,1956 ,    e₂=g( 1,7; 1,2)=0,434.

Tak więc dla obliczenia poprawek //, A: należy rozwiązać układ równań liniowych (14.4.4), _ttóry tutaj przyjmie postać

9,4/i+4,91/c = 0,1956 ,    3,4/i -8,64/c=0,434 .

^związując ten układ otrzymujemy z dokładnością do trzech znaków po przecinku

h= —0,039 , k=0,035.

Uwzględniając wzory (14.4.5) otrzymujemy jako drugie przybliżenie wartości x₂ = l,7-0,039 = 1,661 ,    y₂ = l,2+0,035 = l,235 ,

dokładniejsze niż przybliżenie pierwsze.

Wykorzystując przybliżenie (x₂, y₂) i stosując dalej objaśnioną metodę możemy uzyskać trzecie przybliżenie (x₃, y₃) jeszcze dokładniejsze.

Zadania

14.5.    Równanie x³ - 4x -12 = 0 ma pierwiastek zawarty pomiędzy 2 i 3. Znaleźć wartość pierwiastka z dokładnością do 0,1.

14.6.    Równanie jc³-6x+2 = 0 ma pierwiastek zawarty pomiędzy 0 i 1. Obliczyć dwa lolejne przybliżenia stosując: 1. reguła falsi, 2. metodę Newtona.

14.7.    Równanie x³+2x² + 3x+4 = 0 ma pierwiastek zawarty pomiędzy —2 i —1. Obliczyć go z dokładnością do 0,01.

14-8. Równanie x³ —2x² — 4x — 7=0 ma pierwiastek zawarty pomiędzy 3 i 4. OblU ^ 8° z dokładnością do 0,01.

^ Równanie x⁴ — 2x² + 4x— 8=0 ma pierwiastek zawarty pomiędzy 1 i 2. Obliczyć ² dokładnością do 0,001.

¹ -10 ‘0.01.

j⁴10- Równanie x⁴-3x² + 75x-10000 = 0 ma jeden pierwiastek zawarty pomiędzy

drugi pierwiastek pomiędzy 9 i 10. Obliczyć te pierwiastki z dokładnością

14.11.

h Obliczyć z dokładnością do 0,001 pierwiastek równania x³ — 2x — 5 = 0 zawarty

^lędzy 2 i 3.