155(1)

Różniczkując pochodne cząstkowe pierwszego rzędu względem każdego argumentu, otrzymamy pochodne cząstkowe drugiego rzędu. Oznaczamy je następująco

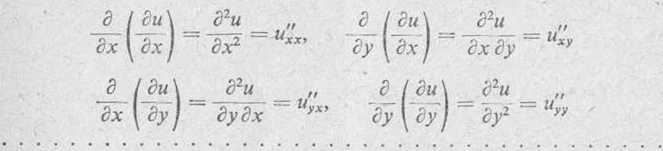
Z kolei różniczkując pochodne cząstkowe drugiego rzędu względem każdego argumentu otrzymujemy pochodne cząstkowe rzędu trzeciego

mentów i każdą z nich również można różniczkować względem każdego jej argumentu.

8 (8²u\ _ ćPtt _    lćPu\ _ JPu_ _ ,,,

,dx \Bx²)~ Bx^{3 Jxxx}' By \8J J ~ Sx²By ~^Jxxy

_B /_d²«_\ _ &^u _    I S²u \ _ _£³w___

By \8xdy] 8xBy^{z xyy,} 8x\8x8yJ BxByBx ^xyx

Analogicznie określa się i oznacza pochodne cząstkowe rzędu czwartego, piątego i wyższych.

Pochodne cząstkowe wyższego rzędu, różniące się tylko kolejnością różniczkowania, jeśli są ciągle, są sobie równe.

Na przykład

(Pu _ B²u    8³u _ 8³u    8³u

8x8y    By Bx ’    Bx²By    ByBx²    BxBydx

Ze stwierdzenia tego wynika, że funkcja dwóch zmiennych z — f(x, y) ma trzy różne pochodne cząstkowe drugiego rzędu

B²z    B²z    B²z

Bx²’    ~8x8y    By²

cztery różne pochodne cząstkowe trzeciego rzędu

8³z c³z    B³z    8³z

3x³’    8x²8y^>    8x8y²’    8y³

i ogólnie n+1 różnych pochodnych cząstkowych rzędu n.

Pochodne cząstkowe wyższego rzędu znajdujemy przez kolejne różniczkowanie pochodnych niższego rzędu na podstawie reguł różniczkowania funkcji jednej zmiennej.

754.    Wyznaczyć pochodne cząstkowe drugiego rzędu funkcji:

1)    z = xⁱ-2x¹y+3y^z, 2) u (x, y, t) = e^xy'.

Rozwiązanie: 1) Wyznaczamy najpierw pochodne cząstkowe pierwszego rzędu, a potem różniczkujemy je ponownie

z’_x — 3.v²—4 xy,    z'y = — 2x²-j-6y

z”_x = 6x- 4y, z_xy = z’;_x = - 4x,    z', = 6

2)    Różniczkując kolejno, znajdujemy

u'_x = yte^xyt,    u’_y = xte^x>’, u\ = xye^xyt

u'_x'_x = yVe^x>\ u'_x'_y = u’_yx = t(l + xyt)e^xyl u_xt = u"_x = y (1 + xyi)e^xyt, u", = u"_y = x( 1+xyi)e^xy’ u,, = x*t²e^xyt, u”, = rye*’¹'

755.    Sprawdzić, czy dla funkcji: 1) z = cos(ax—by), 2) z = ln(x²+y²+1) zachodzi z",, = z"_x.

Rozwiązanie: 1) Różniczkując z względem x znajdujemy z_x = =—nsin (ax—by). Z kolei różniczkujemy z, względem y

(z^)' = z"_y = ab cos (a*— óy)

Różniczkując w odwrotnym porządku, czyli najpierw różniczkując z względem y; Zy = ósin (ax—hy), a potem zj względem .r, znajdujemy

{2% = z"x = ab cos (o.v—by)

Porównując otrzymane wyniki widzimy, że rzeczywiście z"y = z"_x.

2) Przez kolejne różniczkowanie znajdujemy najpierw z_xy, a potem z”_x

2x	1 1
^Zx ~ *^2-i-y^2+i ’	(A-^2+y^2+l)2
^2y	„ 4xy
^? *»+>*+1 ’	~^yx (jc^H-y^2-!-1)^2

Zatem i dla tej funkcji z"_xy = z_yx.

765. Sprawdzić, że funkcja z = 2cos²jy— ^ j spełnia równanie różniczkowe 2 Ą- +    = 0.

dx^l dxcy

313