162

162 Układy regulacji automatycznej

(15.25)    \HUco_a)\~l

(15.26)    arg //(/&'_.) — —n

Zapas modułu wzmocnienia określa się, wykorzystując wartość H( jco,). Wartość    jest liczbą rzeczywistą ujemną. Rozpatrzymy przy

padek, gdy wartość ta jest równa -1. Wartość pulsacji, dla której spełniony jest ten warunek, oznaczymy przez co_;,. Oczywiste jest, że oj„ = co₇ = co_a oraz

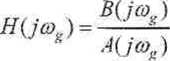
(15.27)

Ponieważ - zgodnie z wzorami (15.1) i (15.2) - wielomian charakterystyczny układu ze sprężeniem zwrotnym jest następujący:

(15.28)    M{s) = M(s) + B(s)

Stąd

(15.29)    MQ&_g) = A{jm_g) + B(ja,_g) = 0

Tak więc ja_g jest pierwiastkiem wielomianu charakterystycznego M(s). Pierwiastkiem jest także wartość sprzężona — jco '■ Fakt. że wielomian charakterystyczny M{s) ma pierwiastki jo)„ oraz -j(o_g . oznacza, iż odpowiedź

układu zamkniętego będzie oscylacyjna, drgania nie będą zanikać, a ich okres będzie równy T„ - Izjco_% .

Otrzymany wynik stanowi potwierdzenie wniosku wypływającego z kryterium Nyauista. że w rozpatrzonym przypadku układ zamknięty jest na granicy stabilności (charakterystyka atnplitudowo-fazowa H(jco) układu otwartego przechodzi dokładnie przez punkt -1 + y'O na płaszczyźnie zespolonej). Zgodnie z tym kryterium dla układu stabilnego wartość H(jco_g) powinna należeć do przedziału (-1,0). Im dalej od punktu -1, tym większy jest zapas (margines) stabilności. W związku z tym praktyczny wzór określania zapasu modułu wzmocnienia jest następujący:

(15.30)    AL = -20log|(H(jct)_x) | [dBj

’ Wielomian o współczynnikach rzeczywistych ma pierwiastki parami sprzężone. Można także sprawdzić, że jeśli Af(ja_g) = ’RsM(jto_i;)+jJmM(jmg) = 0, to także    M(-jw„) =

Rc M (jco_s) - j Im M (jco_g) - 0.