226

450

Rozwiązania i odpowiedzi

8.69.    jc = 28cos(iji + /( • |it) (fc = 0, 1,2) .

8.70. u= -1^3 V 19 + 9^6= -1(1+76)73,    V¹⁹-9^6 = 1(1 _^ x, = u+o= —2yj2, x₂ = y/2 — i, x₃ = j2 + i.

DO ROZDZIAŁU IX

9.24. -60. 9.26. 8. 9.28. 1000. 9.32. 14.

9.23. -10.

9.25. — ayz — bxz - cxy. 9.27. 4.

9.31. 98.

9.33.    (x_A.-x_})((x_i-x₂)(x4-x_z)-2(x₃-x_])(x_A.-x_i)).

II

9.34.    ~ °k, 2n-k+t ^a 2n-k+ 1, k) ■

k= 1

9.37. x = 5, y=-2.

9.35.    x — 3, y= 1.    9.36. Układ sprzeczny.

9.38. Nieskończenie wiele rozwiązań, x = 2y + 5', y dowolne.

9.39.    k = 2, każda para liczb spełnia układ; k = \, układ sprzeczny; przy innych k jedno rozwiązanie.

9.40.    k = 6, nieskończenie wiele rozwiązań, y=~?x + 3, x dowolne, k= — 6, nieskończenie wiele rozwiązań, y — łx— 3, x dowolne; przy    innych k jedno rozwiązanie.

9.41.    x— 1,    y = 2, z = 3.    9.42.    x = |, y= — |, z = 0.

9.43. x — 2,    y = 5, z = 4.    9.44.    x— —9, u= — 3, z = 4.

9.45.    =    x dowolne.    9.46.    x = 2z —|y, i z dowolne.

9.47.    k=2, każda para liczb jest rozwiązaniem; k = —2, x = 0, y dowolne, przy innych k nieskończenie wiele rozwiązań, x = 3(k + 2) y, y dowolne.

9.48.    k = 5, y = 0, x dowolne; k#5, y=Ą(k — 5) x. .

9.49.    Nieskończenie wiele rozwiązań, y~\x, x dowolne.

9.50.    x=0, y=0.

9.51.    k=— 6 albo k — 6, nieskończenie wiele rozwiązań y——\kx\ przy innych ^ mamy x = 0, y=0.

9.52.    Tylko rozwiązanie zerowe x = 0, y = 0.

9.53.    Nieskończenie wiele rozwiązań x = 6y— 3z, y i z dowolne.

9.54.    Nieskończenie wiele rozwiązań x — \y, y dowolne, z = 0.

9.55 Tylko rozwiązanie zerowe x = 0, y = 0.

9.56.    Nieskończenie wiele rozwiązań x = $y, y dowolne.

9.57.    x = 3, y=2, z = 1.

9.58.    z = 22x — 33y— 11; /= - 16x + 24y + 8.

9.59.    Układ sprzeczny.    9.60. Układ sprzeczny.

9 61. z = —x — 2y — 4,5; 1= -2x-4y-12,5; u= -2x-4y-7,5.

9.62.    x = i(8r-6), y=²(l-13t), z = i(15 - 6/).

9.63.    jt = 3, _y = 0, z=—5, r=ll.    9.64. Układ sprzeczny.

9.65.    z = 6-15x+lOy; / = — 7+ 18x- 12y, x i y dowolne.

9.66.    z =13, /= \9-3x-2y, u= -34, x, y dowolne.

9.67.    k= 1, każda para liczb spełnia równanie; k= — 1, x= 1, y dowolne; przy innych k, x=(k+ l)y + A:² + A:+ 1, y dowolne.

9.68. k=2,równanie sprzeczne;k = — 2,x=2, y dowolne; przy innych k,x= —(k+2) y+ +8, y dowolne.

9.69.	"5 2~j fact + by afi + bSl 7 1J ’ |_ca + (i)' cfi + dSj		9.71.
	a b c		a b c
9.72.	x y z u+olx v + ay w+az	9.73.	x+au y+av z+aw u V w

9.74.    Tak, jeśli pierwsza macierz jest wymiaru nxk, a druga kxn, to iloczyn jest macierzą kwadratową stopnia n.

9.75.    1) Aby, iloczyn dwóch macierzy był tego samego wymiaru n x m co pierwszy czynnik iloczynu, drugi czynnik musi być macierzą kwadratową stopnia m; aby iloczyn dwóch macierzy był tego samego wymiaru nxm co drugi czynnik iloczynu, pierwszy czynnik musi być macierzą kwadratową stopnia n. 2) Obie macierze muszą być kwadratowe tego samego wymiaru.

9.76.    Macierz zerowa stopnia czwartego.

9.77. Istnieją obydwa iloczyny:

1 3'	=r^17i |_38 36J ’	'1 3'		'10 15	5'
7 5		7 5		22 25	19
.0 ^2		0 2_	l_3 ^5 U	6 10	2_

, drugi iloczyn nie istnieje .

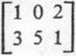
9.78.

x₁a_l+X2^a2 ^xi bi +x₂ 62I yi^ai+y2^a2 .Vi 61+>>262 I z, a_x +^z2 ^a2 ^zi b_x +z₂ b₂J