228(1)

wiamy 1 = n, a jako granice całkowania bierzemy 0 i 2tc\ funkcja ta dana jest bowiem w przedziale (0, 2n). Mamy

On

1_

TC

Zn

j    cos nxdx

* Z

o

1_

2tc

X

n

1

sin/ix--

n

r .    I¹’

| sin nxdx = -

1

2n«¹

cos nx

cos 2nTi— 1 2tui¹

(przy obliczeniu całki zastosowaliśmy wzór na całkowanie przez części).

Dla n = 1,2, 3,... (n ^ 0),    = 0. Gdy n = 0 otrzymane wyrażenie

dla cr„ traci sens. Wobec tego współczynnik a₀ obliczamy osobno. Dla n — 0 mamy cos nx = 1, i ze wzoru (2) otrzymamy

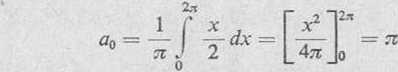
Zn

b_n

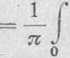
y sin nxdx

dU

1 TsinwA'    xcosnx | _    1

2ti I n¹    n    Jo n

Podstawiając wartości współczynników a_n i b„ do szeregu trygonometrycznego (1) otrzymamy szukane rozwinięcie danej funkcji w szereg Fouriera

+ <o

x ti    \Tsinnx _ tc    sinx sin2x    sin3x

= y J ycos ™* dx = y 11 6cosy— dx-\- I 3*cos dxj = O    'o    2    '

1    I 12 . tmx\ , _ T 2x . tmx , 4 nnxY

= —- — sin — - -}-3 -sin ————^cos — —

2    \_nn 2 Jo l_«7r    2 nn² 2 J₂

n²7i²

(1—costitt); h ^ 0

Dla n parzystych cos nn — 1 i a„ — 0, a dla n nieparzystych cos/irr = Gdy n = 0, ze wzoru (2) otrzymujemy

- \J    rdx= J(j «*+jte*)-iH+łprl- ¹⁵

4 f . nnx ,	1	/ /’ . nnx , ,	f _ . tmx . \
| jsin -2~dx =	2	) 6 sin-	3.vsin — a* 1
b		'ó	2 ^2 '

2

1    T12    7i7ix 1    3 f 4    . nnx    2x    nnx

—    -—cos —    —5—0' sin ---cos ——

2    |_ mi 2 J:    2 |_ n n² 2    mt 2

—    - [12(1 ■—COS/ł7E)-{-3 (4 COS/77T — 8)] =----

2/77T    n7l

Szukane rozwinięcie danej funkcji ma postać

cos

15    12 / nx , 1 3jz.v 1

^J’ ⁼ -2- ⁺ 7n^CM 2 + 9-““-2-+25

inx

--i sin

rr

rrx , 1    . 2n:x , 1    . a ,

+ „-sin -—)-- - sin - ——f- ...

i jest słuszne w całym obszarze określoności funkcji, przy czym w przedziale (0, 2) suma S(x) szeregu jest równa 6, a w przedziale (2,4) suma S(x) == 3x. W punkcie x = 2, gdzie funkcja jest nieokreślona i nieciągła

5(2) = -*- ( lim y+ lim y) = 6

Z x+2-0    2+0

3) W tym przypadku dogodnie jest posłużyć się zespoloną postacią sze-rego Fouriera. Ze wzoru (5) mamy

459

1

2 1 2

n= l

Rozwinięcie to jest słuszne, czyli szereg ten jest zbieżny do rozważanej funkcji, we wszystkich punktach jej obszaru określoności 0 < x < 2n. (W punktach granicznych x = 0 i x — 2n suma szeregu v/ynosi nj2\ w punktach tych wszystkie wyrazy szeregu oprócz pierwszego są równe zeru. Tę samą wartość sumy szeregu we wskazanych punktach otrzymamy z twierdzenia Dirichleta).

2) Korzystając ze wzorów (2), w których podstawiamy / = 2, i dzieląc przedział całkowania (0,4) punktem x = 2 na dwie części (ponieważ w każdej z tych części funkcja jest dana za pomocą różnych wzorów), otrzymamy