0336

337

§ 3. Pochodne i różniczki funkcji wielu zmiennych

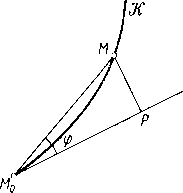
Styczną M₀ T (rys. 99) zdefiniowaliśmy jako graniczne położenie siecznej M₀ M, gdy odcinek M₀M dąży do zera [91].

Można oczywiście dać i taką definicję równoważną z poprzednią:

Prosta M₀ T nazywa się styczną do krzywej JT w punkcie M₀ krzywej, jeśli odległość MP zmiennego punktu M na krzywej od prostej M₀ T, gdy odległość M₀M dąży do zera, jest nieskończenie małą rzędu wyższego niż M₀M (tzn. jeśli stosunek MPjM₀P dąży przy tym do zera(¹)).

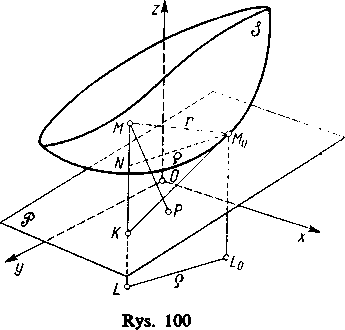
Rozpatrzmy teraz pewną powierzchnię £7 i punkt M₀ na niej (rys. 100).

Analogicznie do definicji prostej stycznej podamy definicję płaszczyzny stycznej.

Płaszczyzna & nazywa się płaszczyzną styczną do powierzchni £7 w punkcie M₀ tej powierzchni, jeśli odległość MP zmiennego punktu M powierzchni £7 od tej płaszczyzny, gdy odległość M₀M dąży do zera, jest nieskończenie małą rzędu wyższego niż M₀M, tzn. jeśli stosunek MP/M₀M dąży przy tym do zera.

Niech [159] powierzchnia będzie określona równaniem z=f(x,y) we współrzędnych prostokątnych.

Weźmy na tej powierzchni punkt M₀(x₀, y₀, z₀) (gdzie z₀=f(x₀, y₀)) i zbadajmy, przy jakich warunkach płaszczyzna 3P, która przechodzi przez punkt M₀ i ma równanie

(6)    Z — z₀ = A(X — x₀) + B(Y — y₀),

czyni zadość tej definicji.

Poprowadźmy prostą ML równolegle do osi z (patrz rys. 100) i poprowadźmy przez M₀ prostopadłą M₀N do ML. Ponieważ odcinek MK różni się od MP stałym czynnikiem różnym od zera, więc zamiast stosunku MP/MM₀ można rozpatrywać stosunek MKjMM₀. Wykażemy teraz, że nie zmieniając w istocie definicji płaszczyzny stycznej, można tu wreszcie zastąpić odległość r=MM₀ odcinkiem p=M₀N.

(‘) Oznacza to, że dąży do zera sin ę, a wraz z nim również kąt <p między sieczną M₀M i prostą M₀ T (patrz rysunek 99).

22 G. M. Fichtenholz