0348

349

§ 3. Pochodne i różniczki funkcji wielu zmiennych

u obliczona na podstawie niedokładnych wartości argumentów będzie także obciążona błędem Au — —f(x + Ax, y + Ay)—/(x, y). Chodzi nam o oszacowanie tego błędu, gdy znane są oszacowania błędów Ax i Ay.

Zastępując w sposób przybliżony przyrost funkcji jego różniczką, co jest usprawiedliwione dla dostatecznie małych wartości Ax i Ay, otrzymamy

du    óu

(16)    Au=—- Ax+—- Ay.

ax    dy

Błędy Ax, Ay jak również współczynniki przy nich mogą być tak dodatnie, jak i ujemne. Zastępując jedne i drugie przez ich wartości bezwzględne dojdziemy do nierówności

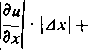
du

dy

■\M-

Jeśli oznaczymy przez du, Sx, dy maksymalne błędy bezwzględne (czyli ograniczenia błędów bezwzględnych), to można oczywiście przyjąć

(17)

du —

dx +

du\

— dy.

oy I

Przytoczymy przykłady.

1) Przede wszystkim za pomocą wyprowadzonych wzorów łatwo jest wyprowadzić reguły znane w praktyce rachunku przybliżonego. Niech będzie u = xy, gdzie x>0, y>0, wówczas du—ydx+xdy; zastępując różniczki przyrostami otrzymamy Au=yAx+xAy (patrz (16)) lub przechodząc do ograniczeń błędów (patrz (17)):

du = ydx+xdy.

Dzieląc obie strony tej równości przez u = xy dojdziemy do ostatecznego wzoru

(18)

du dx dy u x y

który wyraża następującą regułę: maksymalny błąd względny iloczynu równa się sumie maksymalnych błędów względnych poszczególnych czynników.

Można byłoby postąpić prościej — najpierw zlogarytmować wzór u=xy, a następnie zróżniczkować:

lnH=lnx+lny,

du dx dy(^l)

— = —    , itd.

u x y

Jeśli u = xly, to tą samą metodą znajdziemy

du dx dy

ln« = lnx—lny,    —=----i

u x y

przechodząc do wartości bezwzględnych i do błędów maksymalnych otrzymamy znowu wzór (18). Tak więc maksymalny błąd względny ilorazu równa się sumie maksymalnych błędów względnych dzielnej i dzielnika.

2) Często stosuje się dyskusję błędów w miernictwie, głównie przy obliczaniu nie zmierzonych bezpośrednio elementów trójkąta na podstawie elementów zmierzonych. Przytoczymy przykłady z tej dziedziny.

O Zwracamy uwagę czytelnika na to, że różniczkę ln u obliczamy tak, jak gdyby u było zmienną niezależną, chociaż w rzeczywistości jest ona funkcją zmiennych x i y [175]. Uwagę tę należy uwzględniać także niżej.