0338

339

§ 3. Pochodne i różniczki funkcji wielu zmiennych

Gdy spełniony jest ten warunek, współczynniki A i B muszą być równe pochodnym cząstkowym f'_x{x₀, y₀) i f'_y{x₀, y_Q), płaszczyzna styczna wyrazi się zatem równaniem

z - Z₀ =/«(x o, y₀) iX - x₀) +fy(x₀, y o) (Y — y₀).

Zwykle nie piszemy tu wskaźnika przy x, y, z; równanie płaszczyzny stycznej przybiera wówczas postać

(7) Z-z=/:(x,y)(X-x)+f;(x,y)(Y-y).

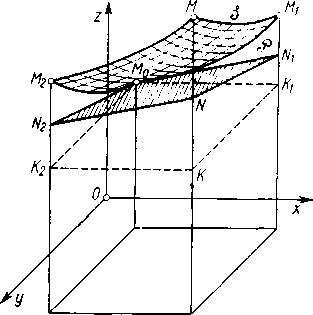
Łatwo widać, że jeśli przeciąć powierzchnię i płaszczyznę styczną dowolną płaszczyzną równoległą do osi z i przechodzącą przez punkt M₀, to jej przekrój z powierzchnią będzie pewną krzywą, a przekrój z płaszczyzną styczną będzie prostą styczną do tej krzywej ł¹).

W szczególności przekrojami powierzchni płaszczyznami y=>’₀ i X=x₀ będą krzywe, których współczynniki kątowe (²) równają się odpowiednio

fx(x₀,y₀) i fy(x₀,y₀)-

Na rysunku 101 odcinki K_tMi i K₂M₂ przedstawiają przyrosty cząstkowe funkcji, a KM — jej przyrost zupełny; odcinki Ki N₁ i K₂ N₂ przedstawiają różniczki cząstkowe funkcji, zaś KN — jej różniczkę zupełną (porównaj ustęp 104 i rys. 44).

181. Pochodne funkcji złożonych. Niech będzie dana funkcja

u=f(x,y,z)

określona w obszarze 3i, przy czym każda ze zmiennych x, y, z jest z kolei funkcją zmiennej t w pewnym przedziale

x=<p(t), y = y/(t),    z = x(0-

Niech oprócz tego punkty (x,y, z) nie wychodzą poza obszar Q> przy zmianie t.

Podstawiając wartości x, y, z do funkcji / otrzymamy funkcję złożoną

u=f(9>(0,V'(t),x(0)-

Załóżmy, że u ma względem x, y i z pochodne cząstkowe ciągłe u'_x, u’_y, w'(³) i że pochodne x\, y‘_t, z, istnieją.

Można wówczas udowodnić istnienie pochodnej funkcji złożonej oraz obliczyć ją.

(‘) Niżej, w ustępie 234, rozpatrzymy ogólniejsze zagadnienie o stycznych do dowolnych krzywych poprowadzonych na powierzchni przez dany punkt.

(²)    Łatwo się zorientować, względem jakich układów współrzędnych obliczamy te współczynniki kątowe.

(³)    Właściwie wystarczy założyć różniczkowalność funkcji u=f(x, y, z).

22*