60

/ 0.

Zatem

dz

WTW

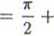
Zadania

Zadanie 6.1

Obliczyć podane całki po zadanych krzywych:

^a)    J \e‘\zdz, C - odcinek o początku —i i końcu 1;

C

b)    J(3* + 1 )^zdz, C - półokrąg {z G C: |z| = 1, Re z ^ 0} o początku —i

C

końcu i:

c)    / e^z dz, C - łamana o wierzchołkach kolejno 0, —, — (1 - *);

J    2 2

c

d)    J (² ~ ^z) dz, C - łuk paraboli y = x² o początku 1 + i i końcu 0;

c

e)    J z Re z² dz, C - ćwiartka okręgu {z G C : \z\ = 2, Re z ^ 0, Im z ^ 0} o po-

C

czątku 2i i końcu 2.

Zadanie 6.2

Obliczyć podane całki po wskazanej krzywej regularnej C o zadanym początku z\ i końcu Z2'.

^a) J ^e'~ dz, z\ — i, z₂ — 0, C - dowolna krzywa;

c

2² cos («z²) dz, z\ = —, z₂ = —t, C - dowolna krzywa;

c

^c) J ^z s'ⁿ z dz, zi = 0, z₂ = —i, C - dowolna krzywa;

c

[ zdz

/ _z2 ₊ 2 ’ ** ~    *² = * ■*" *> C ~ obcinek.

c

Szósty tydzień - odpowiedzi i wskazówki

129

O Zadanie 6.3

Korzystając ze wzoru całkowego Cauchy’ego lub jego uogólnień obliczyć podane całki:

a)    f —-—, C ~ okrąg |z — 3i| = 2 zorientowany dodatnio;

J ZyZ Z2 J

c

f ZG^*^z

b)    /    dz, C - łamana zamknięta o wierzchołkach 0,1 + 2i, —1 + 2i zorien

towana dodatnio;

^c)	/	dz
	1 c	(z^2 + 9)^2’
d)	f	sin z dz
	1 c	(z^2-x^2)^2
^e)	1	e^z dz
	1 c	Z (z — 7Tt)^3
0 Zadanie 6.4

Obliczyć całkę

r, C - okrąg |z — 2j| = 2 zorientowany dodatnio;

zorientowany dodatnio.

I

dz

(z-l)³(z+l)³’

gdzie C jest dodatnio zorientowanym okręgiem o promieniu r i środku z₀, jeśli: a) r < 2, zq = 1; b) r < 2, zq = — 1; c) r > 2, Zo = — 1 lub zq = 1.

Odpowiedzi i wskazówki

6.1 a) 3 - e + i(e — 1); b) (6 + x)i; c) 2e^ — 1 — *e^; d) 1 — |t; e) 0.

_ tr^_

⁶-^{2 a}) *    b) e    -e ⁴ ; c)    (~^^ch| + sh0    i; d) i (ln 2\/2 + i j    - ln 2).

6.3    a) x (cos 2    + «sin 2); b)    xi; c)    d) —e) —-2x^+2

54    2 ir    k⁴

3    3

6.4    a) -x»; b)    c) 0.