DSC07106 (5)

142

Twierdzenia o funkcjach z pochodnymi

• Zadanie 5.8

Obliczyć podane granice. Czy można Lu zastosować regułę de I/Hospitala?

H

.. ..    x + cos 3*    i 2*—sin*

b) lim -—c) lim

zrsm-i) lim:--■

«r?o sin*

»-oo2^r + cos*'

• Zadanie 5.9

Napisać wzory Taylora z resztą Lagrange’a dla podanych funkcji /, punktów x₀

oraz n:
a| /(*) = *^J, *0 = -1| n = 4;	b) /(*) = ^, *o = 1, n = 2;
c) /(*) = sin 2*. *o = *, n = 3;	d) /(*) = e^_I, *0 = 0, n = 5;
^e)/(*) = p*0 = 2,n = 3;	f) /(*) = In*, *o = e, n = 4;
g)/(*) = e“*^I,*o = |,7. = 2;	h) /(*) = ch*, *o = In2, n =
0 /(*) = {'T+z, lo = -2, n = 3	1 j)/(x) = *^3,*o= l,n = 5.

• Zadanie 5.10

Napisać wzory Maclaurina dla podanych funkcji z n-tą resztą Lagrange’a: ») /(i) =sin /?„; b) /(*) = chi, R*;

c) /(*) = cos*, ftn; d) /(*) = ft,.

• Zadanie 5.11

Oszacować dokładności podanych wzorów przybliżonych na wskazanych przedziałach:

- *£2'    B    - -JT

•) <**:»! + —. |*| < 0.1;    b) tg * S8 *, |*| < —;

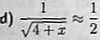
c)\n{l-x)*-x-Ź.-Ź |*| <0.1;

®t^XKX-T⁺W j{fe

o

g) ^l+*ssl + |-—, |*|<j0.25;

* O

f) cos²* =3 1 -i², |z| <0.1;

0 <* <0.1.

• Zadanie 5.12

Stceąjąc wzór Maclaurina obliczyć;

aJsinO.l z dokładnością 10'*; b) I z dokładnością 10'³; c) In U z dokładnością 10'*; d) -^= z dokładnością 10“³; e) {'0997 z dokładnością 10'³; f) cos i z dokładnością 10'*.

Badanie funkcji

Przykłady

Ekstrema funkcji

• Przykład 6.1

Korzystając z definicji uzasadnić, że podane funkcje mają ekstrema lokalne we wskazanych punktach:

»)/(*) = 2 + |* — 1|, x₀ = 1;

— x* dla x 0,

“{i

c) Mx)

0    dla x = 0,

*0 = O;

b) g(x) = 4 - 3x¹⁰°, xo = O;

, . f -x dla x < -1, d) PW= ( ₂-x dla *>-1.

xo = —I.

Rozwiązanie

W myśl definicji funkcja f ma w punkcie zo minimum (maksimum) lokalne właściwe, jeżeli w pewnym sąsiedztwie tego punktu zachodzi nierówność

/(*)>/(*o) (/(x)</(xo)).

a) Wystarczy zauważyć, że

/(l) = 2<2-ł-|*-l|= /(*)

dla wszystkich x j* 1, co oznacza, że funkcja / ma w punkcie zo = 1 minimum lokalne właściwe (rysunek).