DSC07100 (5)

Twierdzenia o funkcjach z pochodnymi

130

»)

• Przykład 5.6 Uzasadnić podane tożsamości:

a)    arcsm -v - ■■ = arccos ■ =i . dla każdego x € |0, oo);

vl + X'    '-yl+ą:²

b)    arctgx= i arctg ~~ dla każdego x G (-1,1).

Rozwiązanie

Wystarczy pokazać, że pochodne funkcji po obu stronach tożsamości są równe na rozważanym przedziale oraz sprawdzić, ze wartości tych funkcji w pewnym punkcie tego przedziału są jednakowe, a) Dla z | [0, oo) mamy

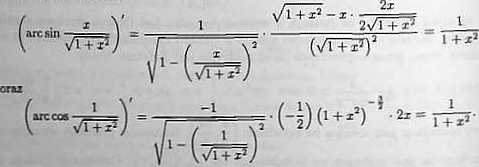
Zatem pochodne są równe pa przedziale (0,oo). Sprawdzimy jeszcze, czy wartości obu funkcji w punkcie 0 6 [0,oo) są jednakowe. Mamy

= 0 oraz

arccoe    = 0.

y/T+IF

Wobec tegp tożsamość jest prawdziwa.

b) Dla z 6 (-1,1) mamy (arc tg z)' = —i—r oraz

i +.Z^-

/i J 2* \' l 1    2(l-*^a)-2r(^2z)    1 _

⁼ 2    / 2z    (l-x*)^a    = l + *^a'

Zatem pocbodoe są równe na przedziale (—1,1). Jak wyżej, sprawdzimy, czy wartości obu funkcji w punkcie 0 € (—1,1) są jednakowe. Mamy

i WBm

arctg0 = 0 oraz    0.

Wobec tegp tożsamość jest prawdziwa.

to

lim

= lim

Przykłady

Twierdzenia o granicach nieoznaczonych

• Przykład 5.7

Korzystając z reguły de L’Hospitala obliczyć podane granice:

131

a) lim o

ln(l + z)

b) lim

lnz

d) lim z I c

ii

o+ Insihz

. .. w-2arctgz

e) lim —-——2—•

o© ln(x + 1) — lnz

c) lim

2^X - 2²“*

-i- (x - 1P *

g) lim ( —r---V l; H) Urn z^-0*:

x—oyzsinz x- J    z—o+

j) lim fcos-^ ;    k) lim (sin*)¹**,

f) lim cos -- ln(l - z);

r—1“ iX

I) JjmO-z)”*;

I) Hm(x + 1)*.

Rozwiązanie

Reguła de t/Hospilala: jeżeli funkcje / i g spełniają warunek lim /(z) = lim o(x) m co

»-*«0    r —jq

lub lim /(z) = lim g[x) = 0 oraz istnieje granica właściwa lub niewłaściwa lim m, ^x—*o    *-*a inzi

/(*). _ *~X₀ «?(*)

Reguła dc r/Hospitała jest również prawdziwa dla granic jednostronnych oraz dla granic w nieskończoności.

a) Urn «~o

ln(l+z)

b) lim

In;

«—o+ In sin z

1

1 +x 0 1

I

"lim

= lim 7-7— = 1.

*—0 1 +X

-00 —co

= “"i ćśx= ^lim (— ■— ) = M = 1.

■ —0+ ^COS— x—0+ V x cos z/

1    2*-2’-* m« (2* + 2^,-*)ln2 41n2    ■

^c) .-T- l^TF 11)=,!LT- ~ 2(,--— -:—=

Uwaga. Jeżeli z —• 1, to rozważana granica nie istnieje.

d) lim x ^e* — 1^

3 = ,iiⁱ?„^£x^L(|]=J“-

= lim e* e^*° s= e° = 1. a v~ao

2 . .

lii

... * (*’ + *) . =.^u-s,i?+r-ⁱ'-