analiza 1 zadania4

150

Twierdzenia o funkcjach z pochodnymi

/'"(*) = e¹ + (x + 2)e* = (x + 3)e^x.

Łatwo teraz zauważyć, że /^w(x) = (x + k)e^z dla k = 0,1,... . Oczywiście powyższa hipoteza wymaga dowodu indukcyjnego. Jednak ten prosty dowód pomijamy. Zatem /** (0) = k dla k = 0,1,... . Tak więc wzór Maclaurina dla funkcji }(x) = xe^x ma postać

₌ 0 + Ix +    +... + ₇^lrx"-¹ + (£±^lx"

1!

2!

x+ ₁₍ +•••+ (_n_2)!

(n — 1)1

ⁿ"^ł (c + n)e^c

nl

nl

gdzie c jest pewną liczbą między 0 i x. c) Dla funkcji /(x) = shx mamy

/'(x) = chx, S'\x) = shx, /'"(i) = chx itd.

Zatem

/^<n> 0

[*)={

sh x dla n parzystego, ch x dla n nieparzystego.

Stąd

/⁽ⁿ⁾(o)

-C

dla n parzystego, dla n nieparzystego.

Wzór Maclaurina przyjmie więc postać

c dla n parzystego, c dla n nieparzystego c dla n parzystego, c dla n nieparzystego,

.    „1 Oj 1    3    xⁿ f sh

sh x = 0 + yjx + x +3jX + -+_¥{_ch x³    xⁿ f sh

^{= i+}3f⁺-⁺^r{ch

gdzie c jest pewną liczbą między 0 i z.

Oszacować dokładność podanych wzorów przybliżonych:

X³ X⁴    7T

a) cosx ss 1 - y + — dla |x| <

Rozwiązanie

a) Aby oszacować dokładność podanego wzoru wykorzystamy wzór Maclaurina dla funkcji /(x) = cos x oraz n = 6. Ponieważ /(x) = cos x, więc f'{x) = - sin x, f"(x) = — cos x, J'"{x) = sini, /^<4)(x) = cosx, /<⁵⁾(x) = —sini, f^(x) = — cosx. Stąd /(O) = 1, /'(0) = /'"(O) = /^<5*(0) = 0, /"(0) = —1, /⁽⁴⁾(0) = 1. Tak więc wzór Maclaurina dla funkcji / ma postać

, i¹ ,    , -cosc |    , x^a , x⁴ , — cosc g

_COsx = 1-y + _¥+—x ₌1_y+24 + Y2Ó-x,

gdzie c jest pewną liczbą między 0 i x. Stąd

COSC Q

’ 720 * I

’-M4)

Przykłady

151

Ponieważ |z|    , więc

1 cos c gl	COSC 6	^1 V
ri2o^x \	“ ~72Q^X <	720	sJ

Zatem błąd jaki popełniamy obliczając wartości cos z dla |x| $5 — ze wzoru przybliżonego

_x³    _X^Ą

_C08SSsl__+_

jest mniejszy niż 0.000029.

b) Aby oszacować dokładność podanego przybliżenia wykorzystamy wzór Maclaurina dla funkcji /(x) = e~^z. Mamy

/'(*) = —e^-x, /"(z) = e^_x, /'"(z) = —e~*, stąd /(0) = 1, /'(0) = -1, /"(0) = 1. Wzór Maclaurina przyjmie zatem postać

7    3

^{= 1 +} TTⁱ⁺2!^{1 +}

3! ^{1 _1 I+} 2 6e^c ’

gdzie c € (0, z). Błąd jaki popełnimy stosując to przybliżenie spełnia nierówność

1

1

10³    6e°    6000'

• Przykład 5.12

Stosując wzór Maclaurina do funkcji:

a)    f(x) = e¹ obliczyć e z dokładnością 10~⁶;

b)    /(z) = vTTx obliczyć \Zl.01 z dokładnością 10^-4.

Rozwiązanie

a) Dla funkcji /(z) = e¹ mamy f^^k\x) = e*, więc /^<ł:)(0) = 1 dla fc = 0,1,... . Zatem wzór Maclaurina dla funkcji /(z) = e* ma postać

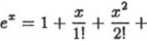
(n — 1)1

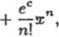
gdzie c jest pewną liczbą między 0 i z . Przyjmując w powyższym wzorze z = 1 otrzymamy

11    1 e^c

^{e = 1 +} iI ⁺ 2!⁺'--⁺(^Tj! ⁺ ^!’

gdzie c jest pewną liczbą z przedziału (0,1). Liczbę e obliczymy z dokładnością 10 ⁶, jeżeli dobierzemy n w ten sposób, aby

= \- <io-®.

I n! |

(¹ + Tl ⁺5l⁺'"⁺(^“Fjl)

Dla c € (0,1) mamy oczywistą nierówność e^c < e < 3. Zatem —j < —. Liczba n € N powinna spełniać nierówność n! > 3 • 10⁶. Ponieważ 10! = 3628800 > 3 • 10⁶ oraz