DSC07145 (5)

218

Całki oznaczone

• Zadanie 8.7 Oszacować podane całki:

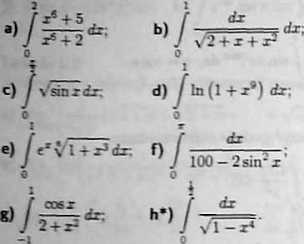
Zadania

219

• Zadanie 8.11

Wykorzystując własności całek z funkcji parzystych, nieparzystych lub okresowych uzasadnić podane równości: i

, [x^s-3x³ + x,    .. Z^- isini    f isinx ,

^a) J x* + 2x² + 1 ^ÓX' ^b) J l+cosi²^^-2./ l + cosi²^’

-i    -*    o

•    ni

c) / In    j-t-.⁵.¹!¹ dx\ d) f (i - £(x))    dx = n    f (x - E(x)) dx, gdzie n 6 N;

J 1 -sinx    J    J¹ "

_i    0    0

i    i ,

/■    j    /" x® dx

e) J e¹ sin x dx = 0; f) j -j=== = 0\

-»    -i

4    4

g) J V-'

x² + 1 cos x<lx

= 2 J '/x¹ + 1 cosxdx;

4*    *

h*)

f—^sln * ^ _ 0; j*) f _x* arcctgidi =

J 1 + cos² x    J    5

T    T

.2004 „:„2003,

j*) J i²⁰⁰³sin³⁰⁰⁴ xdx = J x™*sin™’xdx. -f    -ł

• Zadanie 8.12

Dla podanych funkcji / całkowalnych na przedziale [o, 6], znaleźć funkcje górnej granicy całkowania

Z

F(x) = f f{t)dt, gdzie c 6 [o, 6).

Naszkicować wykresy funkcji / i F, jeżeli:

a)    /(x) = sgn (x-x^a) , |a,6] = (-1,2), c = 0;

b)    f(x) = min{l,x²} [a,6) = [-2,3], c= -2;

II dla -1 < x < 0,

dla 0 < x < 2,

c)    /(*) = { 3x    „ [Ml⁼ I^-1*²!* ^c~ ^-1:

• Zadanie 8.8

Obliczyć wartości średnie podanych funkcji na wskazanych przedziałach:

£^1>V+«- Ki	b) e(x) = sin^3 x,	(<U);
c) w<x) = (łnij,	d) z(x) = arctgz	. [o.Ą.
^e)/w=rf?' 11	f) s(x) = cosx,	tf|=
g) h(x) =xsinz, |0,xj;	h) P(^) — —	t- MI

i

2

1

Zadanie 8.9

a)    Kamień rzuccoo z wysokości h = 2m piooowo do góry z szybkością początkową tsj = 5m/s. Obliczyć średnią szybkość kamienia w czasie rucha (od mementu wyrzucenia do memento upadku na ziemię)- Nie uwzględniać oporu powietrza, przy-jąć ę = 10 m/ s²;

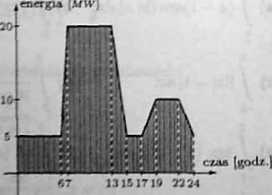
b)    Zapotrzebowanie na energię eiek-tzyezaą w Polsce 13 kwietnia 2003 r. przedstawiono na wykresie: Obliczyć średnie zapotrzebowanie na energię w tym dniu.

• Zadanie 8.10

W Nowy Bok średnia temperatura we Wrocławiu była równa 4° C. Przy czym od północy do godziny 0 rano temperatura była ujemna, a w godz. od 18 do 24 nie Ł, jwlrr^r.ł. y C. Uzasadnić, źe w pewnej chwili temperatura była równa 7° C.