CCF20090120012

mowania: wynika on z fakitu, że odcinek prostej stanowi najkrótszą odległość między dwoma punktami.

A zatem badania nad kształtami różnych przedmiotów mogą nam przynieść dwojaki rezultat:

1)    możemy stwierdzić wiele faktów,

2)    fakty te możemy uporządkować w pewien system ukazujący, co z czego wynika.

Istotnie, obu tych rzeczy dokonali Grecy: ok. 300 r. p.n.e. Euklides napisał swe słynne dzieło o geometrii, porządkując w nim wszystkie znane fakty w postaci systemu. Z dzieła tego możemy dowiedzieć się, dlaczego boki o długościach (3,4,5) dają trójkąt prostokątny; znajdziemy w nim również wyjaśnienie, że takie same trójkąty prostokątne otrzymamy w przypadku innych kombinacji długości boków, np.: (5,12,13), (24, 25, 7), (33, 56, 65).

Wszystko to jednak wymagało czasu. Wielka Piramida została zbudowana ok. 2600 lat p.n.e., wedle zasad wynikających z praktycznego doświadczenia, natomiast system Euklidesa pojawił się dopiero ok. 2300 lat późniejl To niesprawiedliwość wymagać od dzieci, by naukę geometrii rozpoczynały od razu w tej postaci, jaką nadał jej Euklides. Nie można przebyć jednym niejako susem ok. 2300 lat trudów ludzkości. Najlepszy sposób uczenia się geometrii to kroczyć tą właśnie drogą, jaką od początku posuwała się ludzkość: robić różne rzeczy, konstruować je, obserwować, porządkować — a dopiero na końcu rozumować o nich.

A przede wszystkim — nie spieszyć się. Jak łatwo stwierdzić, matematyka nie rozwija się zbyt szybko. Najważniejsze to wiedzieć, czego właściwie dotyczy rozumowanie, mieć w umyśle wyraźny tego obraz. Trzeba wyobrażać sobie różne rzeczy, obracać je niejako w mózgu tak długo, dopóki każde pojęcie nie stanie się zupełnie jasne. Gdy już nauczymy się myśleć wyrazistymi obrazami, będziemy postępować naprzód szybko i bez wysiłku. Ale maszerować naprzód pozostawiając nieprzyjaciela — zamęt myślowy — na swych tyłach, to wprost fatalne. Lepiej zawrócić do tabliczki mnożenia.

KILKA DOŚWIADCZEŃ ZWIĄZANYCH Z GEOMETRIĄ

I. Pewien chłopiec ma listwę drewnianą AC długości 4 tłem. Chce, jak to przedstawiono na ryc. 7, złączyć z nią drugą tak, aby przechodzący na zewnątrz w punktach ABCD sznurek uformował prostokąt.

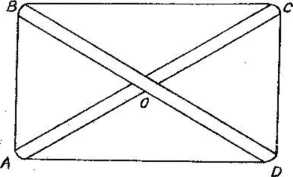
Ryc. 7

Jaka powinna być długość listwy SD? W którym punkcie i(O) należy wbić gwóźdź łączący obie listwy? Czy jest obojętne, jaki kąt tworzą obie listwy ze sobą?

2.    Należy wyłożyć płytkami dany płaski obszar gruntu. Wszystkie płytki mają jednakowy kształt i rozmiary, nie interesuje nas natomiast, jaki będzie kształt „ząbków” na zewnętrznych brzegach pokrytej płaszczyzny. Narysuj możliwie najwięcej sposobów wykonania tego zadania. Jeden z możliwych sposobów przedstawia ryc. 8.

3.    Latarnia uliczna jest zawieszona 4 m nad ziemią. Dziecko mające 1 m wysokości zabawia się starając się chodzić w taki sposób, aby cień jego głowy poruszał się dokładnie wzdłuż linii narysowanej kredą na chodniku. Jak powinno chodzić dziecko, jeśli na chodniku narysowana jest: a) linia prosta, b) okrąg koła, c) kwadrat? Jaka jest reguła określająca wymiary i

27