CCF20090120153

i używa się w przypadku prądów zmiennych, aby pokazać zmiany wytworzone przez włączenie dodatkowego oporu, . indukcyjności itd. W rzeczywistości stosując symbol i porównujemy efekt takich zmian w obwodzie z efektem pewnych zmian (reprezentowanych przez takie znaki, jak a+bi) dokonanych wewnątrz generatora wytwarzającego prąd.

DALSZE BADANIE OPERATORA i

Nie odpowiedzieliśmy jeszcze na jedno pytanie postawione w tym rozdziale, a mianowicie, jak określić e^x, gdy x jest liczbą zespoloną. e^x drukowane grubymi czcionkami jest nową etykietką i moglibyśmy (gdybyśmy chcieli) związać tę etykietkę z dowolną operacją. Ale byłoby to bardzo mylące: musielibyśmy wciąż pamiętać, że wybrana przez nas operacja nie ma nic wspólnego ze zwykłą funkcją e^x i wciąż narażeni bylibyśmy na niebezpieczeństwo popełniania błędów na skutek zapomnienia o różnicy pomiędzy tymi podobnie oznaczonymi wielkościami. Ze względów praktycznych jest więc oczywiście najlepiej nie używać w ogóle etykietki e^x, jeżeli nie możemy znaleźć operacji mającej własności bardzo podobne do własności funkcji e^x.

Znaleźliśmy już operacje, których prawo do etykietek x, x², x³ itd. zostało uznane; wiemy zaś, że e^x można wyrazić przez szereg zawierający x, x², itd. Naturalną więc rzeczą byłoby utworzyć odpowiedni szereg symboli drukowanych grubą czcionką i określić e^x w następujący sposób:

-x⁵ A. •.

e*= i_+x+IxS

Ta definicja jest istotnie całkowicie zadowalająca. Daje nam ona znaczenie operatora e*, o którym można stwierdzić, że ma wszystkie własności zwykłej funkcji e^x.

Ważne jest, aby zrozumieć, co ta definicja zawiera. Gdybyśmy np. chcieli znaleźć e^8+3ł za pomocą tego szeregu, to musielibyśmy zastąpić x przez 2+3i:

_e2_{+3i =} i + (2 + 3i) + |-(2+3i)²+|(2 + 3i)³ + .. .

Musielibyśmy więc obliczyć (2+3i)², (2 + 3i)³ itd., i wyniki podstawić do powyższego wzoru. Okazuje się, że (2+3i)² wynosi — 5+12i, (2+3i)³

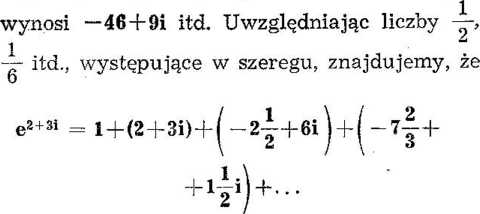
Możemy teraz zgrupować wyrazy zawierające i oraz wyrazy wolne od i; otrzymamy:

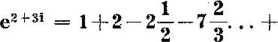
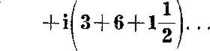
Krok ten jest uzasadniony, gdyż i można traktować tak jak x w zwykłej algebrze, co stwierdziliśmy wcześniej.

Jednakże wynik ten będzie bezużyteczny, do-

309