CCF20140608016

58 5. Wymiary: fraktalny, Hausdorffa i topologiczny

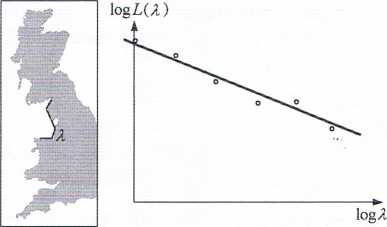
Rys. 5.5. Ilustracja doświadczenia Richardsona brzeża Wysp Brytyjskich oszacowano d ~ 1,25. Oszacowania tego dokonuje się na podstawie kilku pomiarów: dla rozsądnie wybranych wartości A na wykresie zaznacza się punkty x = log A, y = logL(A) i rysuje prostą przechodzącą „jak najbliżej" tych punktów. Nachylenie prostej jest równe 1 — d. Dla małych wartości A liczba

(5.7)

logN(A) ' “ log(l/A)

estymuje wymiar linii brzegowej.

Okazuje się, że dla rozmaitych wysp (a również rzek, ścieżek na górskiej grani itp.) wyznaczony w ten sposób wymiar jest większy od jedności. Obserwuje się pewną korelację między wymiarem brzegu i budową geologiczną lądu.

Przykład ten pokazuje jednocześnie różnicę między wymiarem obliczonym dla obiektów geometrycznych i „wymiarem" zmierzonym dla tworów przyrodniczych, dla których przejście graniczne A —> 0 przestaje być sensowne. Z pomiarów długości L(A) dla kilku małych wartości A trudno jest wnioskować o tym, co się stanie, jeśli A zostanie wielokrotnie zmniejszone.    □

5.3. Wymiar Hausdorffa i wymiar topologiczny

Niech F będzie podzbiorem n-wymiarowej przestrzeni euklidesowej. Pokryciem SB zbioru F nazywamy rodzinę kul A (skończoną lub nieskończoną), których suma zawiera zbiór F. Średnicą tego pokrycia nazywamy średnicę największej kuli rodziny SB. Wprowadzimy oznaczenie

a(d,s)=inf (diamA)^rf    (5.8)

gdzie diam A jest średnicą kuli A £ @S, suma obejmuje wszystkie kule rodziny SB, a kres dolny wybierany jest ze zbioru wszystkich możliwych pokryć SB o średnicach nie większych od e.