CCF20140608�012

54 5. Wymiary: fraktalny, Hausdorffa i topologiczny
kostki Ne(F) ~ 1/e. Jeśli F jest płatem powierzchni gładkiej, to Ne(F) (1/e)2, a jeśli jest obszarem ograniczonym w R3, to Ne(F) ~ (1/e)3. Przybliżenie jest tym lepsze, im mniejsze jest e.
54 5. Wymiary: fraktalny, Hausdorffa i topologiczny
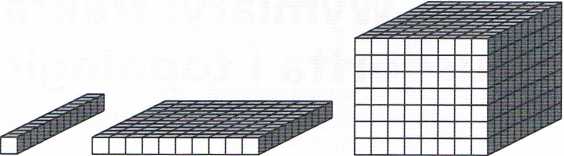
Rys. 5.1. Ilustracja pojęcia wymiaru
Istnieją takie obiekty geometryczne, dla których przy małych wartościach e zachodzi w przybliżeniu proporcjonalność
(5.1)
Ne(F) ~ (l/e)d
i wówczas liczbę d (niekoniecznie całkowitą) można traktować jako wymiar obiektu. Dokładniej mówiąc, wyrażenie nazywane jest wymiarem fraktalnym, wymiarem pudełkowym, wymiarem pojemnościowym (pojemnością) albo po prostu wymiarem, jeśli nie zachodzi niebezpieczeństwo pomylenia z innymi definicjami wymiaru.
Jeżeli zbiór F jest sumą kilku swoich składowych, to
(5.3)
d(Fi U F2 U ... U Fn) = max d(F,)
5.2. Przykłady obliczania wymiaru
Przykład 5.1. Równoboczny trójkąt Sierpińskiego T (rys. 2.5) o boku równym jeden można w oczywisty sposób nakryć trzema kwadratami o bokach równych 1/2 albo dziewięcioma kwadratami o bokach równych 1/4, albo, ogólniej, 3" kwadratami o bokach równych (1/2)”. Przyjmując e = (1/2)", otrzymamy
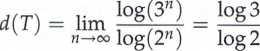
= 1,584962501...
(5.4)
Wyszukiwarka
Podobne podstrony:
CCF20140608�014 56 5. Wymiary: fraktalny, Hausdorffa i topologiczny Rys. 5.2. Pierwsze przybliżenie
CCF20140608�016 58 5. Wymiary: fraktalny, Hausdorffa i topologiczny Rys. 5.5. Ilustracja doświadczen
CCF20140608�011 Rozdział 5Wymiary: fraktalny, Hausdorffa i topologiczny Jedną z najczęściej wymienia
CCF20120509�116 w którym natężenie przepływu Q = nA^/lgz. W ostatnim równaniu A = b(h — ct) jest pol
CCF20101004�022 1.54 8. Przedstawianie danych i graficzne oszacowanie błędu stawiono przykład opisu
CCF20110611�042 - S?> knjjyń Jjl ouOę H
CCF20121215�38 54 • zapis liczby w formie części ułamkowej - mantysy oraz wykładni
CCF20130323�005 54 ĆWICZENIA nie niż tutaj — było powietrze wczesnym rankiem; jak pluśnięcie fali, j
CCF20131013�003 54. Gdzie w genomach najczęściej dochodzi do poślizgu polimerazy?......Wytłumacz 55.
CCF20100503�022 54 Charakterystyka morfologiczna i taksonomiczna porostów i wybranych grup roślin c
CCF20110310�003 4.8.3. Wyznaczanie wymiarów układów uziomowych &n
CCF20111005�021 54 sam okres,co panowanie Szu-iliszu, króla Isinu (1926-1917 p.n.e.)1 Hipoteza Goetz
CCF20111211�050 54 KULTURA POPULARNA 2010 NR I nowanc fotografie, te, które według ich twórców są na
CCF20120509�007 54 Część I. Przykłady i zadania 3.3.14. (Rys. 1-3.40). W naczyniu cylindrycznym o pr
5. (19) Wykorzystanie wymiaru fraktalnego do rozpoznawania rodzaju dna. Wymiar fraktalny to inaczej
100B51 54 4. WymiarowanieW wyjątkowych przypadkach liczby wymiarowe można rozmieścić dowolnie, co po
FRAKTALE Fraktal, obiekt, dla którego wymiar Haiisdorffa-Besicovitcha (tzw. wymiar fraktalny) jest w
CCF20100119�016 54*S 15M o GfeW lj cp4
CCF20100314�005 54 Zagadnienia poprawności leksykalno-semantycznej łości, „nie lgną” do siebie wzaje
więcej podobnych podstron