DSCN0610

256 6. Przekładnie zębate stożkowe

dostosowane do metod obróbki sposoby postępowania przy obliczeniach geometrycznych i wytrzymałościowych, oparte na ich wieloletnim doświadczeniu. Wytyczne te zawierają wzory i współczynniki określające proporcje wymiarowe zębów zestawione w tabelach lub na wykresach, a niekiedy nawet tabele gotowych wymiarów uzębień.

Bliższe dane dotyczące parametrów zarysów stosowanych w różnych systemach uzębień związanych z poszczególnymi metodami kształtowania zębów znajdzie czytelnik w literaturze: [19], [45], [63] i [67].

6.4. Kinematyka przekładni stożkowej

Pojedyncza, trzyelementowa przekładnia stożkowa (rys. 6.15a), składająca się z korpusu O wiążącego koła, zębnika I i koła 2, może być rozpatrywana jako mechanizm o trzech osiach obrotu: a_0l, a₀₂ i a₁₂, przecinających się w jednym punkcie. Osie n₀₁ i a₀₂ są odpowiednio osiami zębnika i koła, a oś a₁₂, stanowiąca linię styku stożków tocznych, jest chwilową osią względnego obrotu kół. Oznacza-

b)

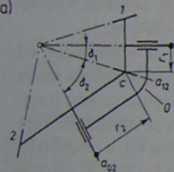
Rys. 6.15. Wykres prędkości kątowej przekładni stożkowej: a) schemat przekładni, b) wykres prędkości kątowej

jąc leżące na tych osiach wektory prędkości kątowej ©_0I, ©₂₀ i co₁₂, można napisać równanie wektorowe:

©oi + ©i 2 + ©20 — 0*

Stąd prędkość kątowa koła, przy znanej prędkości zębnika, wynosi

(6.4)

©20 ^— “ ®12~©01 ©20 ⁼ ©2 0 ©21 •

(6.5)

lub

(6.6)

Zależność (6.6) przedstawiono graficznie na wykresie prędkości kątowych przez wielobok wektorów (rys. 6.15b). Kierunki wektorów są przy tym równolegle do przynależnych im osi a₀i, a₀₂ i «i2 (rys. 6.15a), a zwroty skierowane do punktu wieloboku oznaczonego pierwszą z dwu cyfr oznaczających wektor, np. wektor <pj₀ jest skierowany do punktu 1, a jego koniec znajduje się przy punkcie O.

Według tego schematu można także utworzyć wykresy prędkości kątowych wieloelementowych przekładni stożkowych, zwłaszcza stożkowych przekładni obie-

gowych. Na podstawie wykresu prędkości można łatwo wyprowadzić analityczne związki określające przełożenie przekładni.

Zależność między wartościami kątów stożków tocznych ó₀\ * 602 ^a prędkościami kątowymi co_l0 i co₂o wyznacza wzór sinusów (rys. 6.1Sb):

® o sin5,

-= -—r-.    lo •/)

(Oji> ' sind₂

Z warunku równości prędkości obwodowych na stożkach tocznych w punkcie C:

»cio = «C20 = 'i «io = r₂(o₂₀,    (6.8)

przy uwzględnieniu wynikającej z rys. 6.1Sa zależności

sind₂ sin 61

' (6 9)

oraz proporcjonalności długości promieni r₂ i r₂ obu kół do ich liczb zębów ż, i z₂, można wyznaczyć przełożenie przekładni:

(6.10)

.    <01© __ _ sin<5₂    rj    zj

^: 0)20 sin5,    r₄    z_x

W przekładniach stożkowych bez przesunięcia zarysu lub z przesunięciem zarysu przy x_z — 0 stożki toczne pokrywają się ze stożkami podziałowymi, a kąt osi przekładni jest równy sumie kątów stożków podziałowych:

Z = 5i+5₂.    (6.11)

Wówczas przełożenie geometryczne wynosi

z₂ sin(2T—5.) sinTcosó. — cosZsinó. sinZ •    ,, r

u = — = ——---—-= ——cosZ.    (6.12)

Zi    sin di    sin di    tgd₍

Stąd można wyznaczyć kąty stożków podziałowych:

«. sinZ    . sinZ    .....

tg 51 -- oraz tg<5₂ =—--.    (6.13)

+cosZ    —+cosZ

z_x    Z₂

W przypadku przekładni ortogonalnej, gdy Z = di+d₂ = 90°, przełożenie geometryczne wynosi

_M_£ł_=B!|!i|i ₌ ctgd₁ =tgd₂.    (6.14)

z_x sind,

a kąty stożków podziałowych można wyznaczyć z wzorów:

tg £. = - = — oraz tgd₂ = h = —.    (6.15)

u z₂

17 - Przekładnie zębate