Image84

166

Wobec tego, że ruch translacji odbywa się wyłącznie w jednym wymiarze, składowa prędkości v_x jest równocześnie równa całkowitej prędkości v. Stąd

166

V

mv

X »

P[

Im

mv

~2

dp

mdv

i otrzymujemy

dri

n

m

2    _

mv 2kT

2n kT

dv

Równanie to wyraża liczbę cząstek o prędkości translacji w jednym stopniu swobody między v_x a v_x + dv_x.

Liczba cząstek o module prędkości translacji w jednym stopniu swobody zawartym w przedziale między v a v + dv będzie dwa razy większa i wyniesie

dn"

2 n

m

mv*

2kT

2n kT

dv

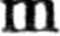
b. Opierając się na uzyskany

otrzymujemy

wyżej wzorze i wobec

n

(nkfy^Tl

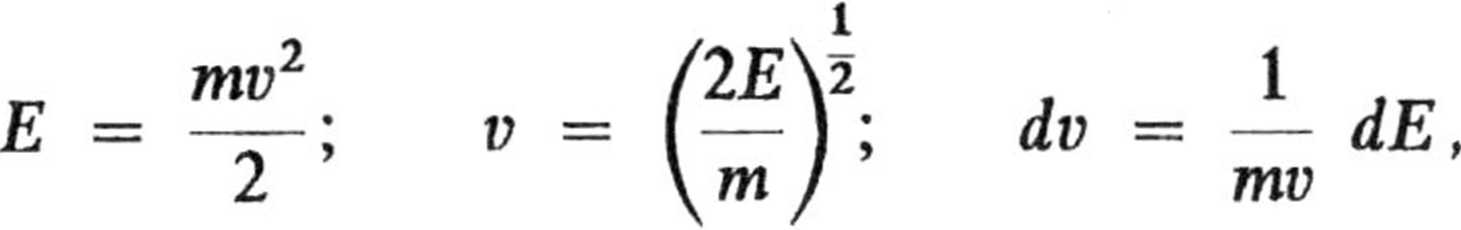
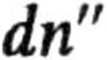
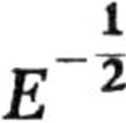
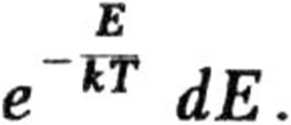
6.6

a. Równanie Maxwella-Boltzmanna na rozkład składowych pędu w u-kładzie o 2 stopniach swobody przybiera postać

1_

2nm kT

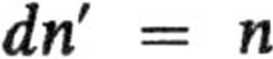
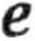
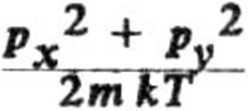
dp_x dp_y.

Wobec

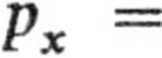
mv_x; p_y = mv_y;

Px + Py ₌ *HI. 2 m    2 ’

<tp_x dp_y = m² dv_y; v² = v_x -f v_y

mv

m

dri

mamy

n ^^{e 2kT} d^vx dv 2n kT    ^{x y}

b. Przechodząc na współrzędne biegunowe u, $ otrzymujemy

dri = n

m

2n kT

mv^z

e ^2kT v dv d&

gdzie

dv_x dv_y = v dv d&.

Całkując wyrażenie na a v -f dv

to równanie względem ,9 w granicach od 0 do 2tc, otrzymujemy liczbę cząstek posiadających moduł prędkości zawarty między v

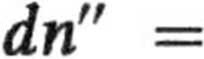
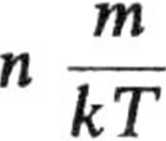
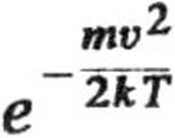
v dv.

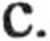
Równanie otrzymane w poprzedni]

punkcie można przedstawić również

w postaci wyrażającej liczbę cząstek posiadających energię translacji w dwóch stopniach swobody zawartą między E a E + dE. Wobec

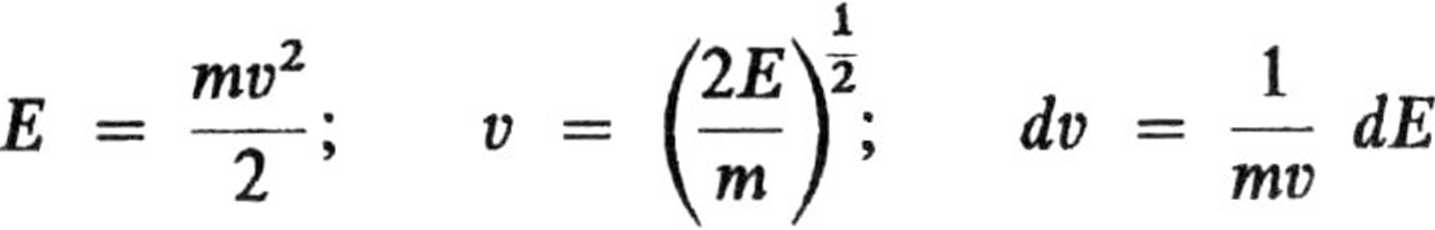
otrzymujemy

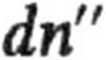
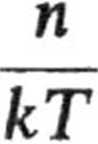
E

e ^kT dE.

6.7

a. dri ~ n

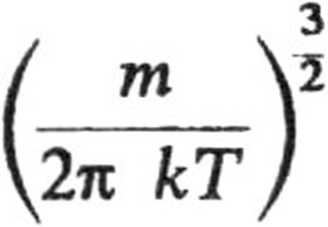
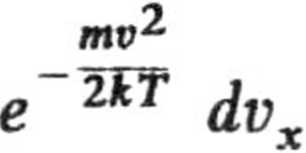
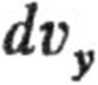
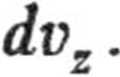
b. Przechodząc na współrzędne sferyczne v, (p i całkując równanie względem 5 w granicach od 0 do n i względem q> w granicach od 0 do 2n otrzymujemy