94101

2

2.1. Prezentacja graficzna

Wobec tego. że funkcja przychodu w warunkach konkurencji doskonałej jest zawsze prostą wychodzącą z początku układu współrzędnych zobaczmy na rysunkach dla jakiej wielkości produkcji dana firma osiągnie największy zysk. gdy funkcje kosztów całkowitych będą się przedstawiać następująco. W pierwszych dwóch przypadkach (rys. 2a i 2b) K_c jest prostą. W trzecim (rys. 2c) koszty całkowite rosną coraz wolniej, w czwartym (rys. 2d) rosną coraz szybciej a w ostatnim piątym przypadku (rys. 2e) najpierw rosną coraz wolniej a później coraz szybciej, czyli tak jak to zostało przedstawione w poprzednim punkcie i na rys. 2 (zob. wykład 8).

Zestaw 4 pierwszych przypadków wyczerpuje wszystkie typy przebiegu rosnących funkcji kosztów całkowitych. Każdy indywidualny przypadek może być potraktowany jako odpowiednie złożenie tycłi czterech wyjściowych Przykładem takiego złożenia jest przypadek 5 przedstawiony na rys. 2e.

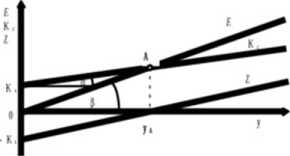
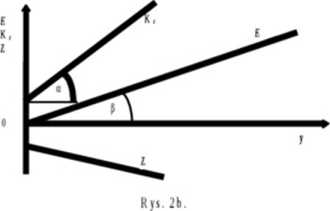
Dwa pierwsze przypadki przedstawione na rys. 2a i 2b charakteryzuje prostoliniowy przebieg funkcji kosztów całkowitych Aby tak było, każdy wzrost wielkości produkcji musi zwiększać koszty całkowite o taką samą wielkość, którą wcześniej określiliśmy jako przeciętne koszty zmienne. Możemy więc powiedzieć, że w obu tych przypadkach przeciętne koszty zmienne były stałe, nie zależą od wielkości produkcji. Oznacza to, że np. ilość surowców, materiałów, energii, pracy i innych zmiennych czynników produkcji, zużywana na wytworzenie jednego produktu jest taka sama, bez względu na to, ile firma produkuje danego dobra, 100 szt. czy 100 000 szt.

Na rys. 2a jest przedstawiona sytuacja, gdy prosta przychodu jest bardziej stroma od prostej kosztów, czyli kąt D jest większy od D. Oznacza to, że przychód całkowity rośnie szybciej od kosztów całkowitych. Skoro koszty całkowite rosną począwszy od wielkości kosztów stałych K& to przetną się z prostą przychodu całkowitego dopiero po osiągnięciu wielkości produkcji y/\. Zysk jest wtedy równy zero. Przyjrzyjmy się temu piuiktowi. Wcześniej stwierdziliśmy, że tg D odpowiada cenie danego produktu. Zobaczmy jakiej innej wielkości odpowiada tg D. Z definicji tangensa wiemy, że będzie się on równał ilorazowi odcinków: Ay^/Oy^ (zob. rys. 2a). Długość odcinka Ay^ to nie tylko wysokość £ osiąganego przy produkcji yĄ ale również i wielkość ponoszonych wtedy kosztów całkowitych K₀ Możemy więc powiedzieć, że tg D w punkcie A jest równy KfJy, co definiowaliśmy wcześniej jako koszt całkowity przeciętny K_Cp.

Reasumując ten wywód możemy stwierdzić, że w punkcie A p = K_Cp. Koszt całkowity przeciętny pokazuje ile przeciętnie koszhije firmę wytworzenie jednostki produkcji. Przypuśćmy, że te koszty wynoszą 5 zł/szt. Jeżeli cena wyrobu jest również równa 5 zł/szt, to łatwo możemy stwierdzić, że ta firma na jednej sztuce nic nie zarabia. Dlatego masa zysku z całej produkcji też musi się równać zero.

Wracając do głównego wątku analizy możemy stwierdzić, że dla mniejszych wielkości produkcji niż yĄ przedsiębiorstwo ponosi straty, które jednak stopniowo maleją. Największe straty firma ponosi dla produkcji równej zero i wtedy wielkością odpowiadają one kosztom stałym. Wzrost produkcji poza yĄ oznacza powstanie zysku, który cały czas rośnie wraz ze wzrostem produkcji.

Warto zauważyć, że tempo wzrostu obu tych wielkości jest w tym przypadku stałe ale różne dla K_c i £. Wiedząc, że £ rośnie szybciej niż K₀ możemy stwierdzić, iż wzrost produkcji o jednostkę wywoła mniejszy przyrost kosztów całkowitych niż przychodu całkowitego. Przypomnimy, że pojęcie kosztów