Scan0012 2

© J. Pelc WMT.doc/23

MOMENTY BEZWŁADNOŚCI FIGUR PŁASKICH. DEFINICJE

Moment bezwładności:

I, = J y

A

1 _y = jx²dA A

I₀ = \p²dA

A

(biegunowy)

	ty	I0 >0
ty-	ło	> ^lxy ('

l_xy = \xydA A

-    względem osi *

-    względem osi y

-    względem p. O

= J(*² +y²)dA = J_x + I_y

A

-    dewiacji (zboczenia)

TWIERDZENIE STEINERA

I* = J y²dA = J (b + y_c fdA =

A    A

- b²1 dA + 2b\ y_c dA + j y²dA = \_x +b² A

A    A    A

= 0 lx_c

Ix = lXc + b^2A	<N -O 1 II
ly~ Iyc + G^2 A	Iyc ^= Iy~ a^2 A

Io ⁼ Jr“dA - l_x + 1^. = I _v + b² A + \_y + a² A - I _v +1y_c + (a² + £²)A - I_c + r² A

A

Ijty = \xydA = j(a + _Xc)(b + y_c)dA = ab\dA + a\ y_c dA + b\ _Xc dA + J_Xcy_c.dA = I_xy + abA ^A A    A ^AS_X=0 ^ASy_e= o ^A

MOMENTY BEZWŁADNOŚCI WZGLĘDEM OSI OBRÓCONYCH

Momenty bezwładności i momenty dewiacji można zestawić w postaci macierzy (tablicy)

(OJ. Fele    WMT.doc/24

Ponieważ składowe tej macierzy zapisane są w układzie (x,y), to przekształcenie Ia=w

wektora a przedstawionego w tym układzie daje wektor w o współrzędnych z tego

samego układu. W celu wyznaczenia momentów względem osi obróconych, określimy

macierz I* w układzie osi    Wcześniej należy określić macierz transformacji wektora z układu obróconego do pierwotnego

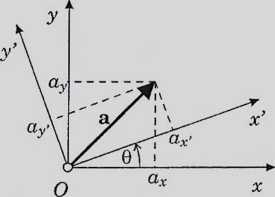
ax		cos#,-sin#	aX'
_<*y.		sin#, cos#	_^ay'_

-> a = Ta'

_T i ₌

a_r = cos#-a„. sin#

a„ = a_Y< sin# + fl„. cos#

y -^v    y

cos# sin# -sin# cos#

la = w -» ITa'= Tw' T^_1ITa'= w* ->    I'a'= w

Ia: Ijcy	cos#,-sin#		I*cos0-Jxvsin#, -(l xsin# + j^cos#)
1 Xy I y _	sin#, cos#		- ix>.cos# +1 vsin#, ix>.sin# +1 vcos#

I_xcos# — I_Xysin#, -(i_Jcsin# + l_A>,cos#)

IT =

cos# sin# -sin# cos#

- I^,cos# + I^sin#, ijy,sin# +1 ,.cos#

]_xcos#-/_xvsin#, — (i^sin# + I^cos#) j, - l_wcos# + i^sin#, l^,sin# + l_v.cos#

Iy = IxCos²^~ I«,sin#cos# -l_x„sin#cos# + I„sin²#

l_x' I v'

cos# sin# -sin# cos#

r'>    1J

V

x y

~ I.r¹ >■’» ł y'

- Ixy ⁼ ~ I-v^sin#cos# - I*,,cos²# + I^sin²# + I _vsin#cos# Iy = I jesin²# - I_xvsin#cos# + l_xvsin#cos# + I _vcos²#

Po uporządkowaniu i wprowadzeniu podwojonego kąta:

= 1