Scan0024 2

X

© J. Pelc WMT/47

Ponieważ

M_g & const [M_g = M_g(x)\,

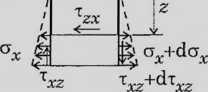
więc naprężenia normalne a_x doznają przyrostu da_x.

Wcześniej wykazaliśmy, że tensor stanu naprężenia jest symetryczny -» _{T x:} = _{T zx} Załóżmy, że r_xz nie zależy odjp, tj. w punktach równo odległych od osi belki naprężenia r_xz maja takie same wartości.

Rozważmy równowagę zakreskowanego elementu: zp_ix = 0:

- \a_xdA + J(cr_Y + da_x )dA -t^ - b-dx = 0

A'

A'

M z

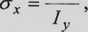
a_x + da_x

(.M + dM)z

dM z

Jda_xdA - r_zxbdx = 0

A'

h

h

dM

dx

h    h

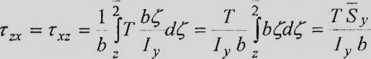
* oś ob.

We wszystkich punktach przekroju leżących na prostej BC

B

<>

z

h

_ 2

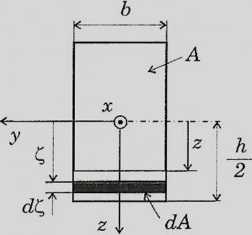
Gdzie S_v =    - moment statyczny odciętej części przekroju względem osi

obojętnej. Przekrój odcięty jest linią równoległą do osi obojętnej położoną w odległości z od niej - czyli przechodzi przez punkt, w którym obliczamy naprężenia styczne.

Przekrój prostokątny:

h

2 2

h

\

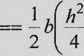
t

J

)bcd(=h(

s;^mx=s_y(z=o)=^ ^"=^_Z = |] = 0

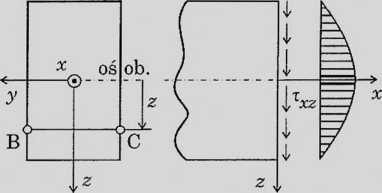
bti

Y _m o max

-max __y __ T',

Iy b

8

bl¹? 12 *

12 T 3 T 8 bh 2 A 2^Tir

-max __

* ~ 2 ^Tśr

Wzór powyższy stanowi więc lepsze przybliżenie wzoru na naprężenia styczne średnie T']

t = — , stosowanego w technicznej teorii ścinania (nity, spoiny).

A)