Scan0031 2

WY BOCZĘ NIE PRĘTÓW ŚCISKANYCH Wyboczcniem pręta nazywamy wygięcie (pierwotnie prostoliniowej) jego osi, wywołane działaniem nań osiowej siły ściskającej. Zjawisko to zachodzi w przypadku, gdy siła ściskająca pręt osiągnie pewną szczególna wartość, zwaną siłą krytyczna.

stany równowagi

t₀ ^{to tk}

fTrfhfrr?

stateczna obojętna chwiejna

Prawidłowo zaprojektowany element konstrukcyjny musi znajdować się w statecznym stanie równowagi. Małe wychylenie elementu ze stanu równowagi nie może powodować dużych przemieszczeń.

©J. Pelc WMT/62

Osiągnięcie przez P wartości 7^. jest praktycznie równoznaczne ze zniszczeniem pręta,

ponieważ na skutek jego wygięcia rośnie moment gnący wywoływany działaniem siły P.

Dla każdego pręta można wyznaczyć (obliczyć) wartość siły ściskającej /V, tzn. taką,

która spowoduje utratę stateczności pręta.

Obliczenia wytrzymałościowe prętów uwzględniające niebezpieczeństwo ich wyboczenia, polegają na takim doborze wielkości statycznych, geometrycznych i materiałowych, żeby spełniony był warunek stateczności

X'P<Pkr

albo

X • (7 < <7_kr

WYBOCZENIE SPRĘŻYSTE. SIŁA KRYTYCZNA EULERA

EJw"(x) = -M(x)

M(x) = Pw EIw"(x) - -Pw

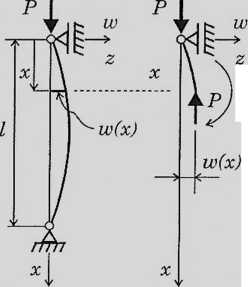
M=Pw

w” + — vi' = 0

i<0)=0

!</)=0

warunki brzegowe

" + k²w = 0, k²

w = As\n1<x + Bcoslcx

vc(0) = A-0+ B-l - 0 -> B = 0 u^?(/) = A sin k/ — 0 —> A = 0

rozwiązanie tiywialne w(x) = 0 (prosty pręt)

vi’(0) = A-0 + B-l = 0 -> B = 0 ] \ p _i n 2 n²EI

,, >-» A—- •i-nn ~>P = n^A ~x

vc(/)= Asmkl = 0 -> sin&/ = 0 -> kl - nz \ . El h

P — p — p ¹ min ¹ n=1 ¹ kr

n²FJ •

p _ __ min

kr ~ ji -

Ponieważ r.r. linii ugięcia belki zostało wyprowadzone przy założeniu małych ugięć, a więc również małych odkształceń i naprężeń, to powyższy wzór jest ważny tylko w przypadku

Pkr < (^akr < )